覆冰输电线结构及载荷对舞动的影响
周坤涛,郝淑英,刘 君,张琪昌
(1.天津理工大学 机械工程学院,天津 300384;2.天津电子信息职业技术学院 机电技术系,天津 300132;3.天津大学 机械工程学院力学系,天津 300072)
覆冰输电线结构及载荷对舞动的影响
周坤涛1,2,郝淑英1,刘 君1,张琪昌3
(1.天津理工大学 机械工程学院,天津 300384;2.天津电子信息职业技术学院 机电技术系,天津 300132;3.天津大学 机械工程学院力学系,天津 300072)
为深入研究导线结构形式对输电线路系统动力学特性影响,以及导线结构形式及气动扭转载荷对覆冰输电线路舞动规律及幅值的影响,采用ANSYS参数化设计语言编写了计算导线舞动的非线性有限元分析程序,计算得出了系统气动载荷作用下的时间历程曲线。发现:在相同的气象条件下,分裂导线的振幅明显大于单根导线,且分裂数越高,导线越容易在短时间内形成稳态的舞动,应尽量采用单根导线或减少导线分裂数;扭转气动力载荷对面内外舞动的规律及幅值影响不大,对扭转角的幅值有较大影响,因此可忽略扭转气动载荷对断线和倒塔的作用。
输电线结构;舞动;有限元;气动扭转载荷;动力学响应
舞动是输电导线在冰,风等多种因素耦合激励下形成的一种低频率(0 Hz-3 Hz),大幅度(数米至十几米)的振动现象。导线舞动的形成机理有Den.Hartog机理、O.Nigol机理和偏心惯性耦合三种。随着研究的深入,发现它们都有明显的局限性,特别是分裂导线,间隔棒,防震锤等出现以后。由于舞动受多种因素影响,发生机理非常复杂,已有的机理学说难以给出合理的解释,采用数值模拟方法研究导线的舞动问题已成为重要的手段。在导线舞动的数值模拟方面,Yu和Desai等[1]提出了导线舞动的三自由度模型[1],Desai提出了一种基于摄动法的舞动数值计算方法[2]。Zhang等[3]建立了混合模型用以研究分裂导线的舞动。该模型假设分裂导线的各子导线同步运动,将分裂导线等效为一根导线在模型中引入无重、刚性、周期性排列的虚拟间隔棒。王丽新,杨文兵等[4]利用梁单元模拟覆冰单导线,探讨了风速、攻角等对舞动的影响。何锃等采用振型叠加法的思想建立了分裂导线舞动的数学模型,并对中山口大跨越三分裂导线的舞动进行了数值分析[5]。严波等人用Hamilton变分原理建立系统的动力学平衡方程,利用罚函数法引入子导线上间隔棒连接点的运动约束条件,利用振型迭加法考虑由于迎风侧子导线尾流对背风侧子导线的影响而出现的作用在两子导线上的空气动力载荷不同的情况[6]。
本文利用有限元分析软件ANSYS建立了覆冰单根、二分裂和四分裂输电线的非线性有限元分析模型,利用ANSYS参数化设计语言编写了计算导线舞动的非线有限元分析程序,研究了系统的动力学特性、导线分裂数及扭转气动载荷对覆冰输电导线舞动规律及幅值的影响。该研究可为输电线路结构的防舞设计提供指导。
1 非线性静力分析
对于输电线路而言,静平衡位置称为体系的静力终态,体系静力终态的内力和几何坐标可作为模态分析,动力分析和其他分析的初态。体系在以静力终态为初态的后续载荷作用下,静力终态的内力作为初应力将对后面的求解产生非线性作用。高压输电线的静平衡是一个大位移,小应变的几何非线性问题,这是由导线的几何特性决定的,几何非线性静力分析的一般公式:
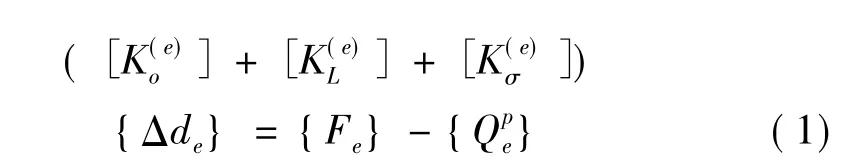

2 非线性动力分析
覆冰分裂导线所受动载荷主要是空气动力载荷,根据流体诱发振动理论,长为L的覆冰导线在速度为U的水平风作用下,所受的空气动力载荷包括阻力FD,升力 FL和扭矩 FM,可分别表示为[2]:
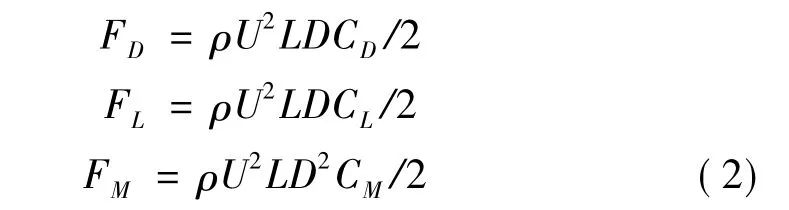
式中ρ为气流密度,D为导线直径;CL,CD及CM分别为升力,阻力,扭转系数,它们与导线截面,覆冰形状和厚度,运动状态以及攻角有关。要得到三个气动系数,必须先确定攻角α,其计算公式为:

式中α0为初始攻角;Δα1为导线垂直振动引起的攻角变化,Δα1=/U;Δα2为导线扭转振动引起的攻角变化,即导线扭转的角度。Δα1不仅影响攻角变化,还影响导线的动态迎风角。所以实际作用在导线的水平力及垂直力为:

非线性动力方程需要迭代求解,现采用N-R法进行迭代,时间积分采用Newmark法,对动力方程进行求解的递推迭代公式为:

其中α,δ是根据积分精度和稳定性要求确定的参数,k为迭代次数。在每个时间步结束后,需要根据导线运动情况重新计算攻角,再通过插值调用新的空气动力系数,改变外载向量做下一步的计算。
3 算例
3.1 输电线的找形
简化模型采用以下3个假设:① 相邻档导线可简化为沿轴向方向的弹簧;② 输电塔为刚性;③ 导线的垂跨比很小。本文只考虑了覆冰单档导线,子导线与间隔棒之间为刚性连接,采用空间梁单元Beam188模拟输电线路及间隔棒,该单元每个节点具有六个自由度,可以模拟输电线水平、垂直、扭转三自由度。采用文献[7]中的方法计算相邻档距的等效弹簧刚度,然后再将其等效成三维空间梁单元的抗拉刚度来模拟相邻档对线路的作用。采用ANSYS参数化设计语言编写了计算导线舞动的有限元程序,导线物理参数如表1所示[3]。单导线及分裂导线的档距相同均为125.93 m。二分裂中的两根子导线的物理参数及初始形状均相同,沿导线方向均匀布置3根间隔棒,每个间隔棒的质量为2 kg,子导线之间的间距为0.4 m。四分裂导线中四根子导线的物理参数及初始形状均相同,沿导线方向均匀布置3根间隔棒,每根间隔棒的质量为7.3 kg,子导线之间的间距为0.45 m。对覆冰单导线、水平二分裂和矩形四分裂导线进行了静力非线性找形计算[8],算法上需要反复更新几何模型,多次进行非线性计算,直到导线的最大位移矢量接近为零,且方向一致,轴向张力与导线初始张力相近时,静力非线性找形分析结束。

表1 导线的物理参数Tab.1 Physical parameters of transmission line
3.2 输电线的模态分析
目前对输电系统模态及固有频率的分析报道基本上是单导线,对分裂导线也大都是将其等效为单导线,而单导线得不到扭转模态。本文采用Block Lanczos算法计算了单导线、双分裂导线及四分裂导线的前四阶固有频率和模态,如表2和图1、图2及图3所示。

表2 导线的前四阶频率Tab.2 Five frequencies of the conductor line

图1 单导线前四阶振型Fig.1 Five mode of vibration of single line
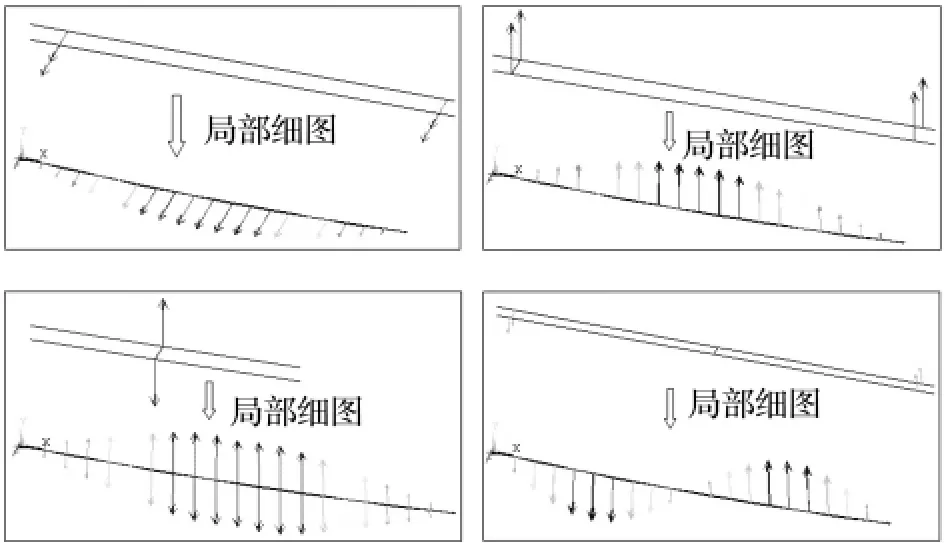
图2 二分裂导线前四阶振型Fig.2 Five mode of vibration of two bundle line
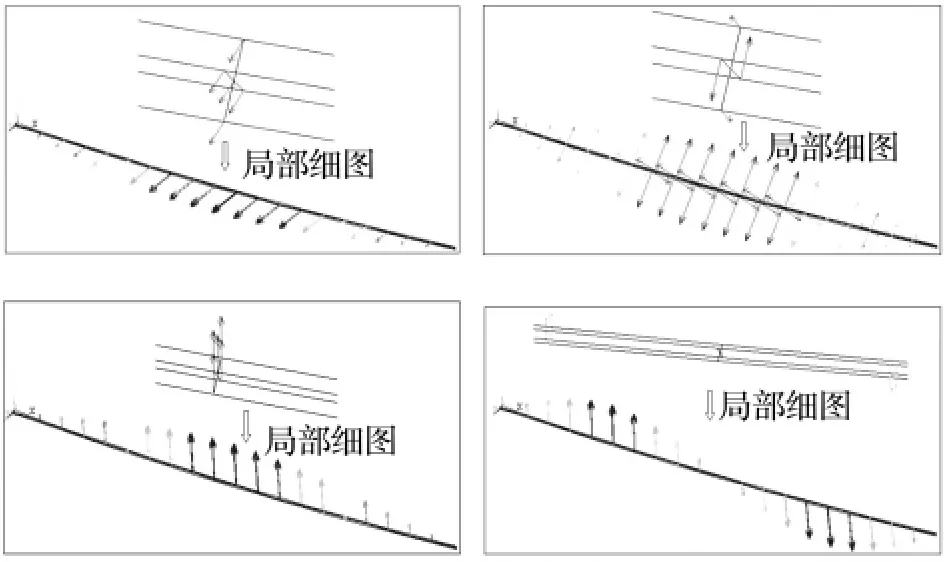
图3 四分裂导线前四阶振型Fig.3 Five mode of vibration of quad bundle line
根据表2及振型图可以看出,面内及面外具有相同模态时其对应的固有频率并不相同,这是由于面内受到重力的影响,改变了导线面内的弹性系数,使得面内固有频率大于面外的固有频率。导线的分裂数对输电线路系统的自振频率影响不大但对振型却有较大影响。单导线、二分裂及四分裂导线的一阶振型相同为面外振动的半波正弦曲线;单导线及二分裂导线的二阶振型相同为面内振动的半波正弦曲线,但四分裂导线为扭转振型;单根导线的三阶振型为面内正弦曲线,二分裂导线则为扭转振型,四分裂导线为面内半波正弦曲线;单根导线的四阶振型为面外振动,二分裂及四分裂为面内振动。本文的模态分析得出了分裂导线的扭转振型,振型的计算结果可为连续体模型中伽辽金离散时模态函数的建立提供依据。
3.3 导线结构类型的影响
图4、图5及图6为本文计算得出的单导线、二分裂导线及四分裂导线中点时间历程曲线,计算时假设覆冰沿线均匀分布,初始攻角为40°,所施加的空气动力参数是在相同气象条件下得出的[3]。二分裂导线及四分裂导线面内舞动的幅值分别为0.366 m和0.389 m,面外舞动的幅值分别为0.023 m和0.079 m,文献[3]采用有限差分法计算了二分裂及四分裂导线覆冰舞动得出面内舞动幅值分别为0.334 m和0.363 m,面外舞动幅值分别为0.020 m和0.022 m,两种方法的计算结果基本一致,验证了有限元分析结果的可靠性。文献[3]中将间隔棒看成没有质量的刚体,本文的有限元分析模型中的间隔棒为有质量的弹性体,这可能是导致两者计算结果出现误差的原因。
从图4~图6可以看出,舞动是一个逐渐形成的过程,开始的时候导线在平衡位置做小振幅的摆动,由于空气负阻尼的影响和风能的积累,水平振幅和垂直振幅逐渐增大,最后受系统阻尼的影响而逐渐稳定。单导线起舞慢,形成稳态舞动所需时间约720 s;二分裂导线起舞较快,形成稳态舞动所需时间约320 s;四分裂导线起舞最快,形成稳态舞动所需时间约160 s。显然,导线的扭转刚度随导线的分裂数的增加而增加,使得导线覆冰易形成翼形断面由风激励产生的升力和扭矩随导线分裂数的增加而增加,因此分裂数越高的导线越容易在短时间内形成大幅舞动,即在大风中形成稳态舞动的概率就越大。分裂导线的覆冰形状决定了分裂导线气动载荷比单导线上大得多,因此单导线舞动幅值仅为0.269,远小于分裂导线面内舞动的幅值。同理可知分裂导线间隔棒安装的数量也会对形成稳态舞动所需的时间及幅值产生影响。因此在线路结构中应尽量采用单导线,必须采用分裂导线的应尽量减少导线的分裂数及间隔棒的数量以减小扭转刚度,减少舞动的发生,减小舞动的幅值。
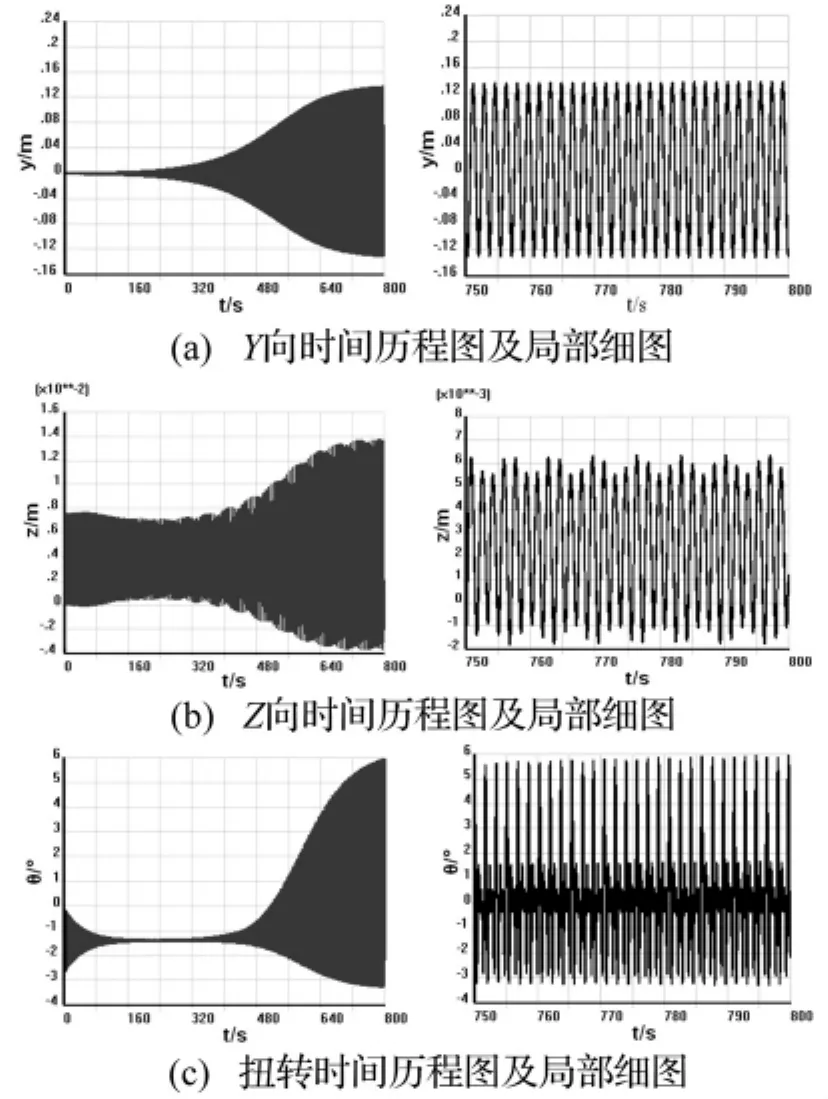
图4 单导线中点时间历程图Fig.4 Time history figure of the middle point of a single line with torsion moment

图5 考虑扭转二分裂中点时间历程图Fig.5 Time history figure of the middle point of twin bundle line with torsion moment

图6 考虑扭转四分裂中点时间历程图Fig.6 Time history figure of the middle point of quad bundle line with torsion moment
3.4 气动扭转载荷对舞动的影响
为研究气动扭转载荷对舞动的影响,本文在相同气象条件和线路结构参数下,只对结构中的各节点施加气动升力和阻力作用,得到了不考虑气动扭转载荷作用时二分裂导线和四分裂导线的时间历程曲线如图7、图8所示。将计算结果分别与图5和图6进行比较可以看出扭转气动载荷对输电线路系统面内及面外舞动的幅值及规律影响极小,但对扭转振动的幅值有很大的影响,两者相差很大,如表3所示。输电线路中相间闪络,金具损坏,跳闸停电,拉断导线和拉倒杆塔等事故,主要是由于舞动幅值过大引起的,扭转气动力偶矩对面内外舞动的规律及幅值影响不大,因此可忽略扭转气动载荷对输电线路舞动引起的断线和倒塔的影响。

表3 气动载荷对分裂导线舞动的影响Tab.3 The effect of aerodynamic torsion loads on galloping amplitude of the bundle conductors
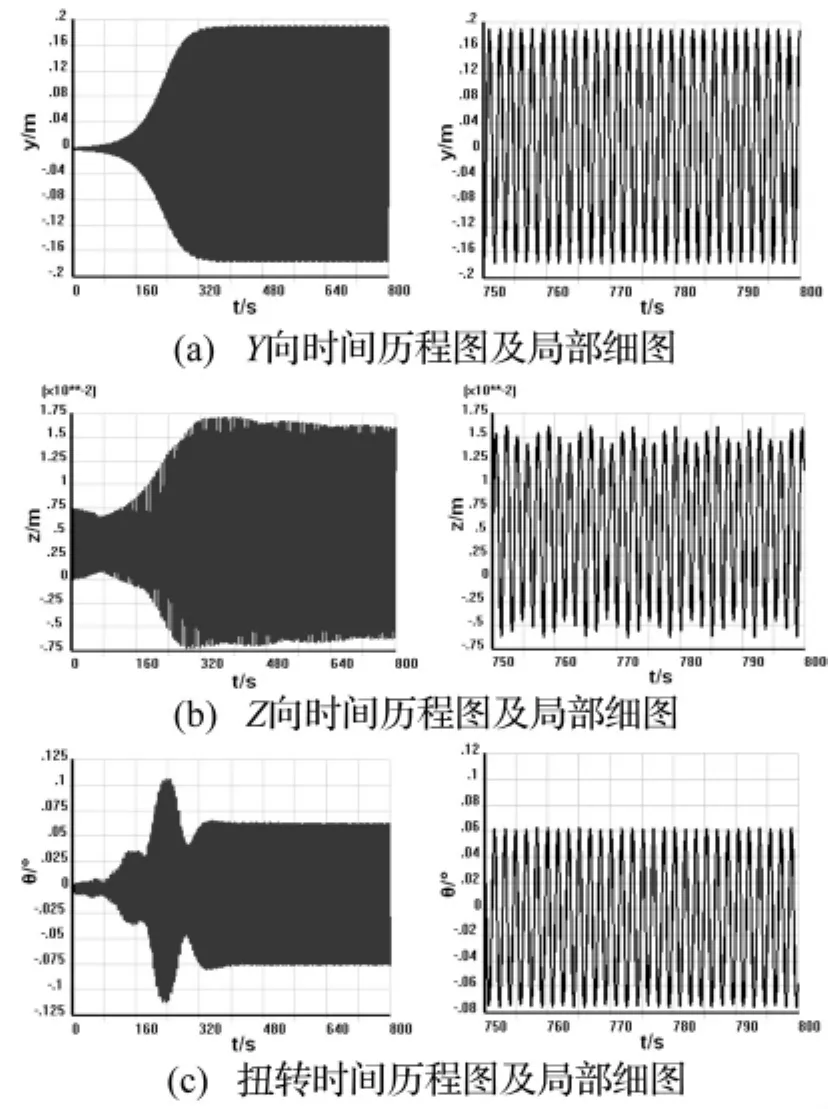
图7 不考虑扭转二分裂中点时间历程图Fig.7 Time history figure of the middle point of twin bundle line without torsion moment
4 结论
采用非线性有限元分析的方法,对单导线、二分裂和四分裂覆冰导线非线性气动载荷作用下的响应进行了分析,提出了分裂导线的扭转模态。分析表明:
(1)在相同的气象条件下,分裂导线的振幅明显大于单根导线,且分裂数越高,导线越容易在短时间内形成稳态的舞动。
(2)面内舞动幅值过大或发散是造成断线及倒塔事故的主要原因之一,扭转气动力偶矩对面内外舞动的规律及幅值影响不大,对扭转角的幅值有较大影响,因此可忽略扭转气动载荷对输电线路舞动引起的断线和倒塔的影响。

图8 不考虑扭转四分裂中点时间历程图Fig.8 Time history figure of the middle point of quad bundle line without torsion moment
[1] YU P, DesaiY M. Three-degree-of-freedom modelfor galloping.Part I:Formulation[J].Journal of Engineering Mechanics,1993,119(12):2404-2425.
[2] Desai Y M,Shan A H,Popplewell N.Perturbation based finite element analyses of transmission line galloping [J].Journal of Sound and Vibration,1996,191(4):469-489.
[3] Zhang Q,Popplewell N,Shah A H.Galloping of bundle conductor[J].Sound and Vibration,2000,234(1) :115-134.
[4]王丽新,杨文兵,杨新华,等.输电线路舞动的有限元分析[J].华中科技大学学报(城市科学版),2004,21(1):76-80.
[5]何 锃,赵高煜.分裂导线扭转舞动分析的动力学建模[J].工程力学,2001,18(2):126-134.
[6]严 波,李文蕴,张宏雁,等.一种模拟覆冰双分裂导线舞动的数值分析方法[J].重庆大学学报,2009,32(7):787-792.
[7] Veletsos A S,Darbre G R.Dynamic stiffness of parabolic cables[J].Int.J.Earthquake Engineering and Structural Dynamics.1983,11:367 -401.
[8]刘 君,郝淑英,周坤涛.空间梁单元模拟覆冰导线静平衡计算的有限元分析[J].天津理工大学,2009,25(6):1 -4.
Influence of conductor structure and loads on galloping of a transmission line
ZHOU Kun-tao1,2,HAO Shu-ying1,LIU Jun1,ZHANG Qi-chang2
(1.School of Mechanical Engineering,Tianjin University of Technology,Tianjin 300384,China;2.Department of Mechanical,Electronic Information Vocational Technology College,Tianjin 300132,China;3.School of Mechanical Engineering,Tianjin University,Tianjin 300072,China)
For profoundly understanding influence of conductor structure forms and aerodynamic torsion loads on dynamic characteristics,galloping law and amplitude of an iced transmission line,a computer program based on nonlinear finite element analysis was developed using ANSYS parametric design language,time history curves were computed.Results indicated that the galloping amplitude of the bundle conductors is obviously greater than that of a single conductor,time needed to enter a steady state of galloping decreases noticeably as more conductors are added;consequently,in the same weather conditions,single conductor and less conductors in bundle should be adopted;aerodynamic torsion loads have slight influence on galloping law and amplitude for in-plane and out-of-plane galloping,but have a greater effect on amplitude of torsion angle;therefore the effect of aerodynamic torsion loads on breaking of an iced transmission line and its towers can be ignored.
conductor structure;galloping;finite element;aerodynamic torsion loads;dynamic response
TM75;O323
A
天津市自然科学基金(11JCYBJC05800);国家自然科学基金(10872141)
2010-07-12 修改稿收到日期:2010-12-30
周坤涛 男,硕士研究生,1985年生
郝淑英 女,硕士生导师,1962年生

