流动性、股票定价及时变性:来自我国沪深股市的经验证据

杨 默，黄 峰

(西安交通大学经济与金融学院，陕西，西安，710061)

一、引 言

流动性是市场的一切，它是资产在短期内以合理价格成交的能力，没有了流动性也就没有了市场，资产的流动性好则意味着资产交易比较容易，从而资产价格也较稳定，交易成本则较低。然而在现实中，流动性具有无法预测的不确定性，因此，流动性的不确定性(流动性风险)可能会影响到资产的定价。经典的资本资产定价模型(如Sharpe、Lintner和 Mossin的 CAPM 模型，Rubinstein、Lucas和Breeden等人发展的基于消费的资产定价模型)能够从理论上解释公司盈利基本面风险和风险溢价之间的关系，却在实证数据上得不到经验支持，很多股价现象无法用经典资产定价模型解释［1－6］。典型的，如Debondt和Thaler等提出的股价过度反应现象及 Mehra和 Prescott提出的等股票“溢价之谜”［7－8］，显然，一定有其他的影响资产定价的因素被忽略了，而资产的流动性风险正是其中的一个重要因素。

为了描述流动性对资产定价之影响，Acharya和Pedersen曾提出了一个经流动性风险调整的CAPM模型，并解释了流动性风险在资产定价中的作用机制［9］。但是他们的流动性风险溢价理论模型存在理论缺陷，其中主要缺陷之一就是他们对证券持有期的外生化处理问题，从而忽略了持有期限内生性的事实。他们简单地假设投资者在第一期购买证券，并在第二期将持有证券一次性卖出，这样的处理高估了流动性交易成本对投资者的影响。作为理性的经济人，投资者完全可以选择对自己最有利的时机出售资产，当市场的流动性较差的时候，投资者可以选择不交易以规避过高的交易成本，或者选择耐心的逐笔分批出售的方式来降低市场流动性枯竭所带来的负面影响。当然，这里并不是说投资者就完全可以规避市场流动性的影响，因为，投资者总会遇到由于财富状况波动或者借贷能力受限而导致的现金需求压力，从而使得资产变现的时间总带有不可控和随机的性质［10－11］)。这就使得投资者对流动性风险的在乎和偏好程度很可能将取决于他的流动性需求状况。

正是由于Acharya和Pedersen没有将投资者流动性需求考虑进去，他们的理论模型无法解释市场流动性水平及风险溢价的时变性现象［9］。但是流动性水平及风险溢价的时变性却是一个异常重要的问题。对于投资者而言，从流动性水平及风险溢价的时变性问题中可以更加精确地识别影响股价的重要讯号，从而选择适当的交易时机，而对监管方而言，从流动性风险及水平的溢价的时变性问题中亦可以找寻调节市场流动性的重要手段，因此，对流动性风险溢价的时变性问题非常值得我们深入的探讨。

为了弥补Acharya和Pedersen的不足，黄峰和杨朝军、邹小芃和黄峰等构建了一个放松的二期迭代模型框架，发展一个新的基于流动性风险调整的资产定价(CAPM)模型［12－13］。该理论模型在投资者同质的假设前提下，将内生流动性风险以及投资者的内生持有期限包括进来，并提出了流动性溢价会随投资者未来流动性需求的紧张程度而发生时变这一理论推断。

但是至今为止，在国内尚无文献对流动性风险问题进行过实证检验，而这正是本文要做的工作，在国内，本文首次对流动性溢价的时变性问题进行了实证研究，特别地，与国外学者的研究相比，本文发现货币供给量的变化对流动性风险溢价具有显著影响。

二、经流动性风险调整的CAPM模型及待检验命题

邹小芃、黄峰等用一个简单的两期迭代模型推导了流动性溢价的时变性命题［13］。其基本思想如下:假设在第t期存在若干个完全同质的投资者，市场上存在共j个股票。投资者通过优化消费投资行为实现自身的效用最大化。在第t期，投资者根据自己的初始禀赋决定消费与投资的分配比例，而在第t+1期投资者则根据自己的流动性需求状况做出卖出证券的决定，投资者的目标是要实现两期效用的最大化。投资者的流动性需求状况分为紧张状态和不紧张状态，在上述两种不同状态下，投资者对股票流动性的偏好和需要有所不同。在流动性紧张的状态下，投资者对流动性有着特别的偏好，投资者流动性越是紧张，投资者对股票流动性的边际效用越大，投资者对股票流动性越是在乎，进而导致了流动性溢价的时变性(包括流动性水平溢价的时变性和流动性风险溢价的时变性)。

(一)理论模型的基本型态

邹小芃和黄峰等对传统的CAPM模型加入流动性风险的调整，构造了一个流动性溢价模型①详细推导过程见邹小芃、黄峰、杨朝军:“流动性风险、投资者流动性需求与资产定价”，《管理科学学报》，2009年第2期，这里仅列出基本型态，不再赘述。:

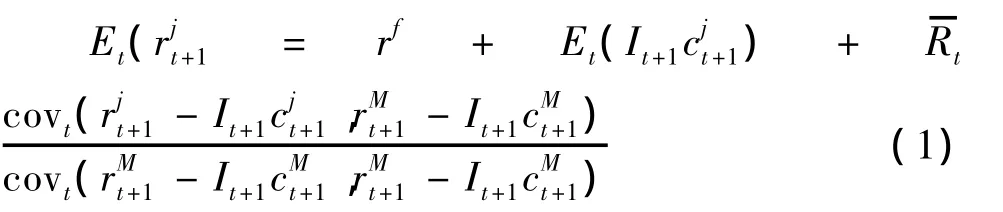
或者等价地表示为:

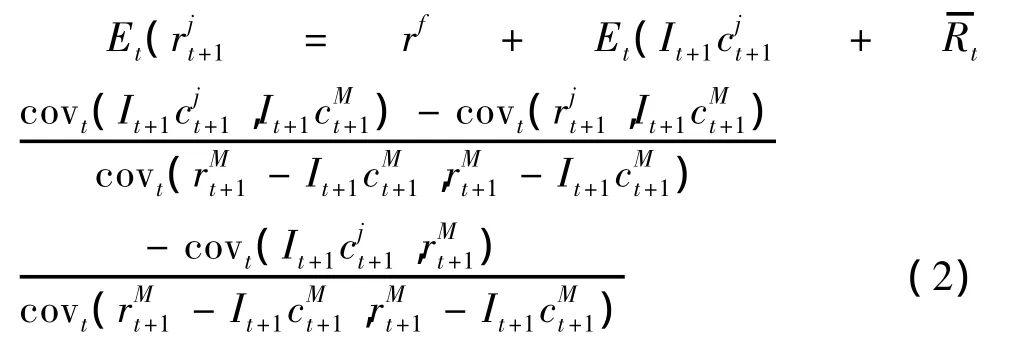
(1)式和(2)式中，rf为无风险利率;为股票j交易前毛回报率;It+1为状态变量，当It+1=1时，表示未来流动性需求为紧张状态，这里假设紧张状态出现的概率为λt+1，而当It+1=0时，表示未来流动性需求为不紧张状态，其发生概率为(1－λt+1);为股票j在t+1期流动性紧张状态下的非流动性交易成本;用状态变量与非流动性交易成本的乘积It+1表示股票j在t+1期的非流动性交易成本，显然当It+1=0时，It+1=0，而当流动性需求紧张(也即It+1=1)时，It+1为非零的正数为市场组合在t+1期的毛回报率;It+1则是市场组合在t+1期的非流动性交易成本=E－－trf)为风险溢价。

公式(1)即是说，股票j在t+1期的期望回报率由无风险利率rf和流动性水平溢价以及风险溢价构成。

其中股票j的流动性水平溢价为Et()，股票j的风险溢价为是对股票系统性风险溢价的测度。

公式(2)则是对公式(1)的具体分解，它将风险溢价分解为价格系统风险溢价和流动性系统风险溢价。

其中covt()则是被经典CAPM深刻讨论的价格风险敏感度，是对单纯的系统性价格风险的度量，在下文中我们用β1i来简化表示。而covt(It+1，被 称之为流动性三个协方差，是对流动性系统风险的相关测度，为了简便起见，下文我们分别用和表示。

因此我们有以下待检验命题:

投资者会对预期流动性交易成本要求溢价补偿，对单纯的系统性价格风险要求风险补偿，对投资净收益中不可分散的流动性风险要求风险补偿。

而且，从(1)和(2)式可知，流动性水平及流动性风险的溢价受状态变量It+1的影响，因此流动性水平及风险的溢价会随It+1的概率值的变化而具有时变性。λt+1越大，表示投资者未来流动性需求紧张的可能性越大，变现其所持股票以补充流动性的可能性越大，因而，股票流动性水平及流动性风险的溢价应该越大。

(二)实证检验模型的设计

为了集中分析流动性水平及流动性风险溢价的时变性问题，并为了方便回归检验，我们用如下更为简单的方程式替代理论模型(1)和(2)式进行实证检验:

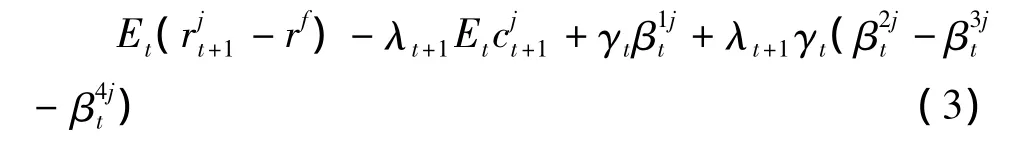
此即为用于检验流动性水平溢价及流动性风险溢价时变性的基础模型，其中，γt为股票的共同系统因子为股票的市场Beta和为股票的3个流动性Beta，流动性需求紧张状况的概率λt+1分别以系数形式出现在股票流动性预期水平(也即)和代表股票流动性风险的三个beta(即和)前面:

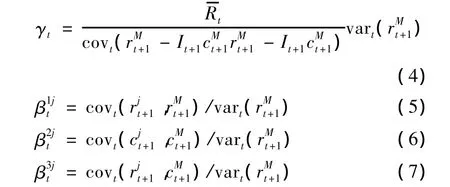
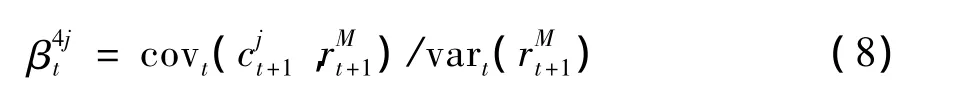
三、实证分析

(一)工具变量的选取

由于投资者的流动性需求紧张状态的概率分布是无法直接取得的，所以必须用适当的替代工具变量来代理理论模型中的变量，我们选择了分别反映宏观经济、金融以及股市的状态条件。

1.宏观经济变量

我们选择M1的月增长率来作为宏观经济变量代理变量。由于M1由硬币、纸币和活期存款的总和构成，所以，M1能代表宏观经济中货币流动性的充足程度。M1供应越大，投资者的流动性越充足，从而未来流动性需求的紧张概率越低，从而对流动性的偏好下降，流动性的边际效用也就越小，从而对非流动性水平及风险的溢价要求减少，此时，股价将上升。此外，也可以选择M2作为货币供给指标，运用效果应是类似的。因此，我们认为，投资者对非流动性水平和风险的溢价要求和货币供应量成反比。

2.“先行指数”变量

“先行指数”(LEAD)是中国国家统计局公布的一种用于反映未来经济变化趋势的合成景气指数。其合成的指数包括:①恒生内地流通股指数，权重7.867%;②产品销售率，权重15.08%;③货币供应M2，权重 15.734%;④新开工项目，权重 15.734%;⑤物流指数，权重13.767%;⑥房地产开发投资先行指数，权重10.487%;⑦消费者预期指数，权重9.33%;⑧国债利率差，权重12%。“先行指数”值的大小标志着未来经济的景气度，指标值越高，未来越景气，指标值越低，未来越不景气，当未来景气度较低时，投资者月可能面临资金紧张从而需要变现资产的情况，从而导致资金紧张的概率增大，进而进一步导致投资者对非流动性的单位风险溢价要求的提高。所以，我们预期“先行指数”与非流动性单位溢价以及流动性风险单位溢价之间成负相关。

3.银行间月平均拆借利率

1996年1月中国人民银行正式成立了全国统一的银行间同业拆借中心，并发布了同业拆借加权平均利率(CHIBOR)。理论上来讲，同业拆借利率能够在一定程度上动态地反映一个国家借贷资金的充裕或者紧张情况，同业拆借利率越高，说明资金越短缺，对应于投资者未来资金需求紧张的概率就越高，反之，同业拆借利率越低，说明资金越宽裕，对应于投资者未来资金需求紧张的概率就越低。在概率越高的情况下，投资者对流动性越渴求，从而流动性的边际效用越大，导致对非流动性的单位风险溢价要求也更高。所以，理论上我们预期同业拆借利率与非流动性水平以及单位风险的预期回报率是正相关的。

4.市场状态变量

我们用市场组合收益率的波动(VOL)来测度市场状态。Chen和HongStein等以及Connolly和Stivers等认为收益率的波动率反映了市场的不确定程度［14－15］。当市场收益率波动较大时，意味着市场的不确定性增加，从而导致投资者对未来变现需求紧张的概率的增加，这会引致对股票非流动性单位溢价要求的提高。与此观点一致的还有Vayanos，该学者亦认为流动性风险溢价往往受到市场收益率波动的影响［16］。他构建的理论模型证明，当基金管理人受到出资人压力而赎回现金时，在收益率波动较大的环境下，基金管理人将变得更加厌恶风险，并对流动性好的资产有着特殊的偏好，从而导致流动性风险溢价的提高［16］。因此，理论上来讲，我们预期股价波动率与单位非流动性水平和风险的预期回报率之间是正相关的。

(二)非流动性的测度

在实证研究中，我们无法直接对股票的非流动性交易成本进行计量，所以我们采用非流动性指标来替代股票非流动性交易成本的概念。在本文中我们用个股月度非流动性指标来计算，时间序列分析所用的个股月度非流动性指标是由价格振幅除以交易金额构成，具体结构如下:

(三)回归检验模型

这里假设未来流动性需求紧张的概率λt+1与4个工具变量是线性的函数关系，用下面的线性方程来表示:

其中，k0到k4是待估计的系数。结合方程(3)和(10)，设立检验时变性命题的基本回归方程如下:

对流动性水平和风险溢价的时变性的检验可以通过对系数k0到k4和b0到b4的估计来进行，基本原理如下:

1.对流动性风险溢价的时变性命题。通过对b1－b4的估计来检验，如果b1－b4都不显著，说明流动性风险溢价的时变性命题得不到支持，反之，若b1到b4中有显著不为零的，则说明流动性风险溢价随着某个工具变量的变化而变化，时变性命题获得了数据的支持。

2.同理，流动性水平溢价的时变性命题则通过对k1到k4的估计来检验，k1到k4显著则流动性水平溢价的时变性得到支持，反之，则得不到支持。

估计方法采用pool估计法中的SUR方法，估计时矫正了扰动项的时期异方差和自相关性。在利用股票横截面和时间序列数据进行估计的时候，k0到k4和b0到b4都是固定的待估计系数。而其它待估计的系数(包括a1、b5t、b6t和 b7t)则是时变的，意思是检验期间相应第t月份都有一个系数估计值和。为检验这些系数的显著性，在得到估计值的时间序列之后，计算它们在时间序列上的平均值以及相应的t统计量，通过t统计量检验这些系数是否显著不为零。

(四)数据

1.样本数据。考虑到2006年和2007年股权分置改革的影响，为了保持条件的稳定性，本文截取了1995年1月3日至2005年12月30日我国沪深股市的日交易数据和财务数据，数据来自“万得资讯”。经过以下步骤的处理，研究期间共有136～912个股票达到以下条件:

第一，为排除股票操纵和坐庄从而不能真实反映流动性水平的干扰，特别剔除了ST股、PT股和长期停牌股票;

第二，剔除被媒体曝光以及曾连续发生3个以上跌停板但并没有证据显示当时公司经营状况有明显变化且与整个大市走势不相符的股票;

第三，剔除股票刚上市交易第一个月的数据，并且如果在某个月内的交易不足15天则剔除该股票在此月的数据。

上述样本股票代表了研究期间内各时期的整个市场组合。为使检验结果有更好的可靠性，需要保证用于时间序列分析的股票有较长的上市时间，因此，我们在市场组合中选取1996年以前上市的136个股票，而且用这些股票的月收益率对月流动性水平及其风险等变量指标进行计量分析，验证本文的命题。

2.工具变量数据。货币供应量M1和同业拆借加权平均利率(CHIBOR)月指标数据来自“万得资讯网”，“先行指数”(LEAD)数据来自于国家统计局网站，与 Fujimoto和 Watanabe(2005)的方法相类似，月波动率指标(VOL)用我们的市场组合收益率计算，即每个月内市场组合的日收益率的样本方差。

4.股票的4个风险敏感度beta用第t个月以前的12个月的日收益率数据和日非流动性数据进行计算，并要求12个月内有效交易天数至少150天。

(五)实证检验结果分析

1.平稳性及相关性检验

单位根检验的结果显示，除股票市场组合收益率的月波动率(VOL)之外，工具变量M1(货币供给量)、同业拆借平均利率以及“先行指标”的时间序列数据都明显表现出了服从单位根过程的特征，因此，对M1变量、同业拆借平均利率变量以及“先行指标”(LEAD)变量需要进行差分处理，其中M1变量的月增长率依然服从1阶单位根过程，所以对M1变量再进行一次差分处理，计为“dM1”，对同业拆借平均利率的一阶差分计为“dCHIBOR”，对“先行指数”进行一阶差分计为“dLEAD”。经差分处理后的4个工具变量月指标时间序列数据跨度为1996年12月－2005年12月。单位根检验显示它们都是平稳过程。见下表:

表1 平稳性检验

表2则列出了经差分后的4个工具变量之间的相关关系，可以看出，4个变量间不存在显著的相关性，从而避免了回归估计时的共线性问题。

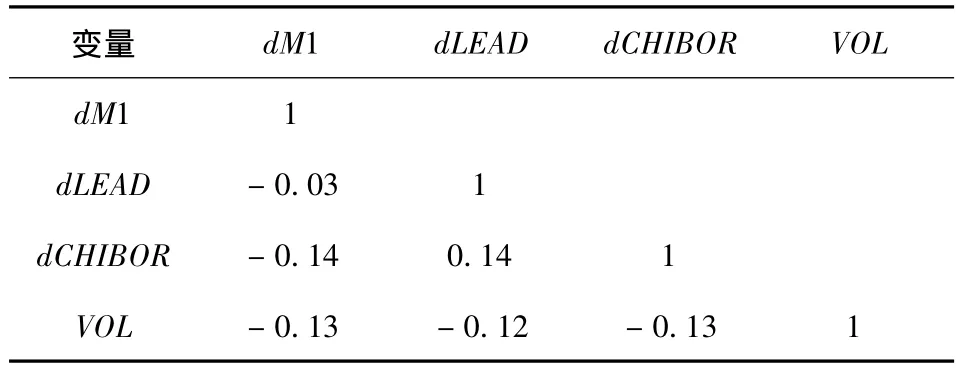
表2 工具变量之间的Pearson相关系数

2.对回归方程(11)的回归检验

表3给出了对基本方程(11)分10个模型分别进行回归检验的结果，10个模型估计的调整后的拟合优度R2都在75%以上，这说明回归方程(11)具有非常好的解释力。

从模型1的回归结果来看，货币供给dM1和“先行指数”dLEAD的系数k1和k2的估计值分别为－0.12和－0.358，并且在5%的水平上显著通过了检验，和理论预期一致，货币供给量越大、未来景气越好，投资者对单位非流动性水平的溢价要求越低。但银行同业拆借平均利率(dCHIBOR)和市场波动率(VOL)的系数估计值不显著。

为了对4个工具变量分别单独进行流动性水平溢价时变性检验，我们分别设定了模型2－模型5，检验结果显示，dM1和dLEAD的系数依然能够显著地通过检验(详见模型2和模型3)，符合理论预期，对银行同业拆借平均利率的系数估计仍然不显著(见模型4)，而市场波动率(VOL)的系数估计则变得显著了，为0.072，也即市场收益率越不确定，投资者对单位非流动性水平的要求收益率越高。从而可以看出这4个工具变量对流动性水平溢价的影响力，货币供给量M1和未来景气状况最能影响流动性水平溢价，市场波动率其次，同业拆借率则几乎没有影响。

有一个现象值得注意，模型1－模型5的回归检验都是在同时将非流动性水平变量illiqjt和流动性风险变量β234，jt纳入的回归检验，但由于流动性风险变量取决于流动性水平变量，回归之间存在一定程度的共线性，这导致对b0－b5的估计可能不准确，检验结果也显示只有b1的估计值是和理论预期是一致的，其他的系数则未通过检验。也就是说流动性水平变量的存在会影响到对流动性风险变量系数的估计，但反过来，流动性风险变量的存在却不影响流动性水平变量系数的估计。为了避开流动性水平变量对流动性风险变量系数估计的干扰，模型6－10，剔除了流动性水平的变量，而且单独检验了流动性风险变量的系数估计结果，以便验证流动性风险溢价的时变性命题。

表3 回归方程(11)的估计结果

当剔除了流动性水平变量后，b0－b5的估计值变得显著不同于模型1－模型5的估计值，其中b0的估计值为0.441，这和流动性风险溢价为正数的理论预期完全一致。而不论是模型6还是模型7均显示货币供给量M1的系数为负数，并显著地通过检验，从而印证了货币供给量越大时，流动性越宽裕，投资者对流动性的需求越低，投资者对流动性风险的溢价要求也越低这一理论逻辑。但是其他工具变量的检验结果没有达到我们的理论预期，其中dLEAD指标没有得到预期为负的结果(详见模型6和8)，市场波动率指标在模型6中显著通过检验，但在模型10中却不显著，特别是银行同业拆借利率指标dCHIBOR的检验结果和预期完全相反，这可能和我国银行业拆借市场交易不活跃从而不能真实反映资金紧张程度有关。

虽然个别指标没有能够完全符合我们的理论预期，但总体来讲，我们不难发现，货币供给量、先行指数和市场波动率都能非常好地解释流动性水平溢价的时变性，而货币供应量指标则能非常好地解释流动性风险溢价的时变性。也即是说，流动性风险水平溢价的时变性命题以及流动性风险溢价的时变性命题得到了实证数据的有力支持。

四、结 论

通过货币供给量M1、“先行指数”、银行间同业拆借平均利率以及股价波动率作为反映投资者未来资金紧张程度概率的工具变量，本文检验了证券流动性溢价(包括流动性水平溢价和流动性风险溢价)的时变性命题，其结果显示:货币供给量M1、“先行指数”以及市场波动率动能很好地解释证券流动性水平溢价的时变性，货币供给量越大、未来景气越好、市场波动性越小，投资者对证券单位流动性水平的溢价要求越低，反之，货币供应量越小、未来景气度越差、市场波动性越高，则流动性水平的溢价越高;而在证券流动性风险溢价的时变性方面，货币供给量M1则表现出了更为一致和显著的解释力，即货币供给M1越宽裕，那么投资者流动性越高，对证券流动性的波动越不在乎，对证券的单位流动性风险的补偿回报率要求越低，所以证券市场就会上涨，反之亦然。

上述检验结果同时也印证了我国股市一直被称之为“资金市”的看法，证明了过去一段时间里，股市价格确实与货币供应量的变化有显著的正向关系，货币供应量通过影响流动性(水平和风险)的单位溢价对我国股市存在不可忽视的影响。

［1］Sharpe W.Capital asset prices:A theory of capital market equilibrium under conditions of risk［J］.Journal of Finance，1964，19:425 －442.

［2］Lintner J.The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets［J］.Review of Economics and Statistics，1965，47:13－37.

［3］Mossin J .Equilibrium in a capital asset market.Econometrica［J］.1966，35:768 －783.

［4］Rubinstein M.The valuation of uncertain income streams and the pricing of options［J］.Bell Journal of Economics，1976(7):407－425.

［5］Lucas R E.Asset prices in an exchange economy［J］.Econometrica，1978，46:1429－144.

［6］Breeden DT.An Intertemporal asset pricing model with stochastic consumption and investment opportunities［J］.Journal of Financial Economics，1979(7):265 －296.

［7］De Bont W，Thaler R.Does the stock market overreact［J］.Journal of Finance，1985，40;793 －805.

［8］Mehra R，Prescott E.The equity premium:A puzzle［J］.Journal of Monetary Economics，1985，15:145 －161.

［9］Acharya V V，Pedersen LH.Asset pricing with liquidity risk［J］.Journal of Financial Economics，2005，77:375－410.

［10］Huang M.Liquidity shocks and equilibrium liquidity premia［J］.Journal of Economic Theory，2003，109:104－129.

［11］Lynch A W，Tan S.Explaining the magnitude of liquidity premia:The roles of return predictability，wealth shocks and state － dependent transaction costs［R］.NBER Working Paper，No.10994，2004.

［12］黄峰，杨朝军.流动性风险与股票定价:来自我国股市的经验证据［J］.管理世界，2007(5):30－48.

［13］邹小芃，黄峰，杨朝军.流动性风险、投资者流动性需求与资产定价［J］.管理科学学报，2009(2):56－68.

［14］Chen J，Hong H，Stein J C.Forecasting crashes:Trading volume，past returns，and conditional skewness in stock prices［J］.Journal of Financial Economics 2001，61:345－381.

［15］Connolly R，Stivers C，Sun L.Stock market uncertainty and the stock － bond return relation［J］.Journal of Financial and Quantitative Analysis，2005，40:161 －194.

［16］Vayanos D.Flight to quality，flight to liquidity and the pricing of risk［R］.NBER Working Paper，No.10327，2004.