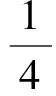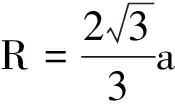圆在物理解题中的应用赏析

赵斌

(长沙市第六中学 湖南 长沙 410000)

圆是完美的象征，在物理学中圆的知识应用非常广泛.下面赏析圆在物理解题中的巧妙应用.

1 用半径表示大小相等的矢量

由三角形知识求出正确答案是选项A，C.

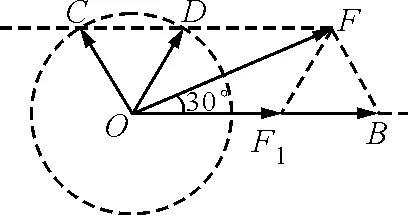
图1

2 用弦设置运动的比较

两个重要结论：

(1)物体从竖直圆环的顶点沿任何弦由静止开始无摩擦下滑到圆周上，所用的时间都等于它沿圆的直径做自由落体的时间.

(2)物体从竖直圆环的圆周上沿任何弦由静止开始无摩擦下滑到圆周的最低点，所用的时间都等于它沿圆的直径做自由落体的时间.

【例2】如图2所示，由竖直墙壁和斜坡构成一凹形槽，竖直墙壁和斜坡相交于O，从墙的最高处A到斜坡有两条光滑轨道AB，AC，已知OA=OB，C点在B点的下方.两小孩同时从A处开始自由滑下，问两小孩谁最先滑到斜坡？

图2

解析：该题似乎少了条件，给思维造成了很大障碍.如果应用上面结论的(1)，该题可即刻求解.

因OA=OB，故可以O点为圆心，OA为半径作圆，AB为圆的一条弦，由结论(1)可知，沿AB滑下的小孩比沿AC滑下的所用时间长，即沿AC滑下的小孩先达到斜坡.

【例3】如图3所示，在同一竖直线上有A,B两点，相距h，B点离地高度为H.现要在地面上找到一点C，使得物体由静止沿从A,B两点分别向C点安放的光滑木板滑动时，满足运动时间相等.求O到C的距离.

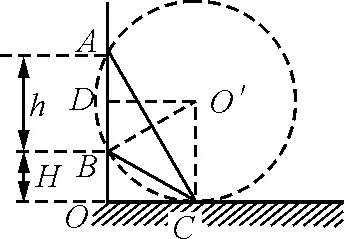
图3

解析：由结论(2)可知，该题中涉及的A,B,C三点分别是竖直圆周上的三个不同位置，其中C点是最低点,AC和BC分别是圆的两条弦.画出过A,B两点并与地面相切的圆，切点即为满足题设条件的C点.由几何关系有

由直角三角形知识有

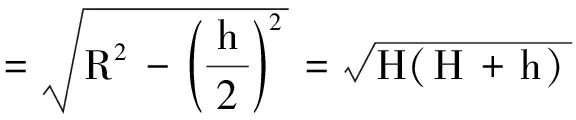
3 用切线求解最值问题

【例4】如图4所示，在匀强电场中，将一电荷量为q,质量为m的小球由静止释放，带电小球的运动轨迹为一条直线，该直线与竖直方向的夹角为θ.下列对电场强度大小说法正确的是

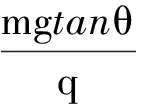
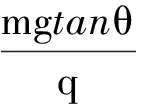
D.以上说法都不正确

图4

解析：由题设可知，带电小球受重力和电场力作用，且合力方向与运动方向相同，即与竖直方向成θ角.根据力的合成法则可知，电场方向不是唯一的并且没有最大值，故选项A,B错误.在图4中，以重力的末端为圆心画出与合力相交的所有圆中，合力方向与圆相切时对应的电场力最小，由三角形知识可知这一最小值为mgsinθ，故选项C正确.

4 用对称性挖掘隐含条件

【例5】如图5所示，正方形匀强磁场区域边界长为a，由光滑绝缘壁围成.质量为m，电荷量为q的带正电粒子垂直于磁场方向和边界从下边界正中央A孔射入磁场中，粒子碰撞时无能量和电量损失，不计重力和碰撞时间，磁感应强度大小为B，粒子在磁场中运动的半径小于a.欲使粒子仍能从A孔射出，粒子的入射速度应为多大？在磁场中运动时间为多长？

图5

解析：当粒子垂直于磁场方向进入磁场且只受洛伦兹力作用时，粒子的运动轨迹是圆(或圆弧).粒子从A孔射入又要回到A孔，经历了什么样的路径？这是本题的难点，同时也是题设中一个关键性的隐含条件，要突破这一难点，必须用到圆运动的对称性.当粒子垂直于边界进入磁场时，必定经过一系列对称形式的运动才有可能回到出发点.粒子的运动可能是图6(a)、(b)两种形式(这种对称性构成了一幅美丽的“窗帘”).

图6

由于粒子速度的大小并未确定，图6(a)的运动形式中粒子的碰撞次数是多种可能的.由几何关系可知，粒子做圆周运动的半径可能为

又

所以

(n=0,1,2…)

同样，对于图6(b)的运动形式，粒子的碰撞次数也是多种可能的，且当粒子恰好运动到正方形的顶角并反弹后，由于粒子受到的洛伦兹力垂直于竖直边，粒子只可能沿着竖直边做匀速直线运动，由几何关系可知粒子做圆周运动的半径可能为

又

所以

(k=1,2…)

5 用相切圆的特性化解难点

图7

解析：该题的难点是如何确定速度最大的带电粒子做圆周运动时圆心的位置.

粒子在磁感应强度为B的匀强磁场中运动半径为

(1)

速度小的粒子将在x

轨道半径大于a的粒子开始进入右侧磁场，考虑r=a的极限情况，这种粒子在右侧的圆轨迹与x轴在D点相切(虚线圆)，OD=2a，这是水平屏上发亮范围的左边界.

速度最大粒子的轨迹如图8中实线所示，如何确定这一临界状态的粒子打在屏上的位置,找到它的轨迹圆心是关键.它的轨迹由两段圆弧组成，即两圆相切于M点，根据相切圆的特点：两相切圆的圆心与切点必在同一直线上.由此可知，两段圆弧的圆心必在过M点的直线上，设圆心分别为C和C′，又由于左边圆弧的圆心在y轴上，两圆弧半径相等，由对称性可知C′在x=2a直线上.

设t1为粒子在0a区域中的运动时间，由题意可知

由此解得

(2)

(3)

由式(2)、(3)和对称性可得

∠OCM=60°

∠MC′N=60°

∠MC′P=150°

所以

∠NC′P=150°-60°=90°

设速度最大值粒子的轨迹半径为R，由直角三角形COC′可得 2Rsin60°=2a

得

由图8可知OP=2a+R，因此水平荧光屏发亮范围的右边界坐标为