关于速度选择器的两个“定论”

曾湘咏

(株洲市教育科学研究院 湖南 株洲 412000)

1 两个“定论”

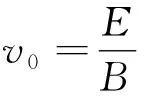
图1

(1)它们都不能由缝S2射出；

这种定性分析“自然而合理”地成为了上述两个“定论”的主要依据，两个定论也显得“毋庸置疑”．然而，除了能判断这些粒子的运动轨迹是曲线外，关于它们运动的其他细节，如轨迹方程、运动性质、运动范围等，我们却知之甚少．要对这两个“定论”做出评判，需要对带电粒子在速度选择器中的运动做必要的定量分析．

2 问题探究

2.1 粒子的运动方程

为便于分析，暂不考虑速度选择器的尺寸．设带电粒子的电荷量为+q，质量为m，入射速度为v0．以入射点为坐标原点O，初速度方向为x轴正方向，垂直于v0且指向D1板为y轴正方向建立平面直角坐标系，如图2所示．图中vx，vy和Fx，Fy分别表示粒子运动到P点时的速度和所受洛伦兹力在x轴和y轴方向上的投影，其中Fx=qBvy，Fy=qBvx．根据牛顿第二定律，在x轴方向有

图2

在y轴方向有

做适当运算得二阶微分方程

方程的通解为

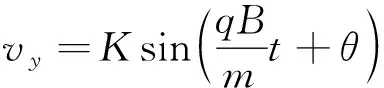
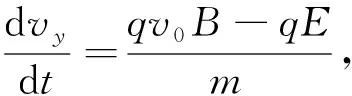
(1)

(2)

利用初始条件t=0，x= 0，y=0，得

(3)

(4)

式(1)～(4)描述了粒子分别在x轴方向和y轴方向的运动规律．

2.2 粒子的运动性质

2.3 粒子的运动轨迹

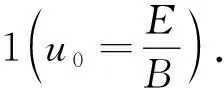
表1 轨迹与对应的速度值

图3

图3有着丰富的内涵．

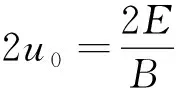
2.4 结论

3 速度选择器的理想尺寸

(5)

(6)

以质子为例，其质量和电荷量分别为m=1.67×10-27kg，q=1.60×10-19C，若E=1.67×104V/m，B=0.167 T，可计算出