用电容器的电阻和电容特性公式计算非平行板电容器的电容
葛松华 唐亚明
(青岛科技大学数理学院 山东 青岛 266042)
许多文章[1~6]对非平行板电容器的电容进行了计算,方法不尽相同,但结论一致,这对教学讨论来说是非常有意义的.本文再给出一种方法,就是根据电容器的电阻和电容特性公式,即电容器的漏电电阻R与电容C的乘积等于其间电介质的电阻率ρ与电容率ε之积
RC=ρε
(1)
如果计算出电容器的漏电电阻R,则可得到其电容C,反之亦然.
1 电容器的电阻和电容特性公式
任何两个导体,无论其形状、尺寸如何,当它们用绝缘体分隔时,就形成一个电容器,讨论电容器的介电性和导电性,就是讨论其电容和电阻[7].
如图1所示,设一电容器中间充满各向同性的均匀电介质,其电容率为ε,电阻率为ρ.电源连接在电容器上时,两导体极板分别带电+Q和-Q.

图1 电容器示意图
两导体构成两个等势面,其间存在静电场,两导体间的电势差
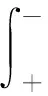
导体上的电荷
Q=∬SσdS=∬SεEndS=ε∬SE·dS
则其电容为
(2)
如果中间的电介质不是理想的绝缘材料,两导体间将形成通过绝缘材料的电流,则电介质显示出一定的电阻,这个电阻常称为漏电电阻,用R表示.
由于两导体间有电势差
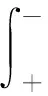
则电介质中的电流
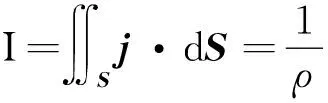
根据欧姆定律,导体间的电阻
(3)
由式(2)和式(3)可得
RC=ρε
上式即为电容器的电阻和电容特性公式,它对所有的电容器都成立.
2 非平行板电容器的电阻和电容
设非平行板电容器两极板的长为l,宽为L,两极板延长线交于O点,夹角为θ,其横截面如图2所示.极板窄端和宽端到原点O的距离分别为R1和R2,且L=R2-R1,极板的长和宽都远大于板间距离,可忽略边缘效应.
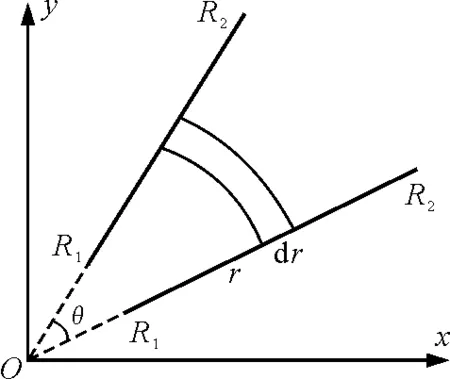
图2 非平行板电容器示意图
如图2,在两极板间r处,取宽为dr的一段圆弧状的小体积元,该小体积元的面积为ldr、长为rθ,其电阻
两极板之间的电阻可视为无限多小体积元电阻的并联,根据电阻的并联公式可得
则非平行板电容器的漏电电阻
(4)
根据式(1),得到非平行板电容器的电容
(5)
这与用其他方法所得结果相同.
3 结束语
电容器是电磁学中的一个重要模型,也是电子技术中的一个重要器件,根据电容器的电阻和电容特性,如果知道了电阻可求得其电容,反之亦然,尤其是对一些计算复杂的模型来说,此方法简单易行.在教学过程中,用此种方法计算或估算一些电磁参数是非常有实际意义的. 另外,在实验中可以用稳恒电流场的模拟法得到不同模型的电阻值,从而求出其电容[8].
参考文献
1 郑民伟.非平行板电容器电容和电场的一种计算.大学物理,2001,20(2):17~18
2 秦德培.非平行板电容器电容和电场的简化计算.大学物理,1995,14(1):13~14
3 李建青,马争争,田旭.非平行板电容器电容和电场的两种计算方法之讨论.大学物理,2008,27(8):27~28
4 王利敏,李长群,赵双义.非平行板电容器电容的又一算法.大学物理,2006,25(4):13~14
5 葛松华.非平行板电容器电场和电容的另一种计算.大学物理,2004,23(11):34,41
6 郑民伟.非平行板电容器电场和电容的进一步计算.大学物理,2010,29(12):10~11
7 贾起民,郑永令,陈暨耀.电磁学(第二版).北京: 高等教育出版社,2001. 378~379
8 (美)William H.Hayt,(美)Jr. John A. Buck著.徐安士,周乐柱译.工程电磁学(第六版). 北京: 电子工业出版社,2004. 134~136

