关于两道磁通量判断题目的对比实验证明
吕争光
(安徽省濉溪二中 安徽 淮北 235100)
在高中物理电磁感应一章里,有这样两道有关磁通量判断的题目.
【例1】当一个线圈平面与条形磁铁的轴线垂直(如图1,注意线圈套在磁铁上),并且沿平行于轴线方向从磁铁一端移到另一端的过程中,穿过线圈的磁通量是如何变化的?

图1 图2
【例2】水平放置的扁平条形磁铁,在磁铁的左端正上方有一线框,线框平面与磁铁垂直,当线框从左端正上方沿水平方向平移到右端正上方的过程中,穿过它的磁通量的变化是
A.先减小后增大 B.始终减小
C.始终增大 D.先增大后减小
如果问线圈中的感应电流方向可由楞次定律判断,即感应电流的磁场总是阻碍引起感应电流的磁通量的变化.因此,只要知道了磁通量的变化,便能判断出感应电流的方向,故归根结底还是要判断出磁通量如何变化.
对于例1,各种资料基本上都能给予统一的解释.画出条形磁铁周围的磁感线分布图,因为条形磁铁内部的磁感线从S极指向N极,而外部磁感线从N极到S极.且内部密集,外部相对较稀疏,在中间最稀疏.故在线圈处于条形磁铁中间位置时,在线圈内且在磁铁外区域的磁感线较少,又因为分别向两个相反方向穿过同一个面的磁通量可以相互抵消.故在线圈处于条形磁铁中间位置时磁感线抵消得少,即剩余的磁通量多.因此,线圈位于条形磁铁中间位置时磁通量大.用这个理论便很容易解释,当线圈套在条形磁铁上且位于中央位置时,如将线圈面积扩大,则磁通量抵消得多了,故合磁通量将减少,可总结为环套磁铁,合磁通两边小,中间大,且环大合磁通将减小,若环无限大,则合磁通为零.
但用这个理论解释例2时便出现了问题,因为此时合磁通量已无抵消的情况.按照中间磁感线稀疏的结论,中间的磁通量应该最少.然而,不少资料书却给出了磁通量中间最大,持此种观点的人认为中间的磁感线和线圈平面垂直,而两边的不垂直,故中间的磁通量最大.
笔者又查阅了不少资料,其中部分资料对此避而不谈,而通过网上检索和搜集的资料来看,认为线圈位于条形磁体中间位置时磁通量大和认为线圈位于条形磁体中间位置时磁通量小的都占有较大的比例,且众说纷纭.为了搞清结果,笔者带领学生上了一节探究课,课题为“探究两种情况磁通量的变化”,因为实践是检验真理的唯一标准.
从哪开始探究呢?经过思考,该课题探究参考了楞次定律的研究过程,即因为磁场和磁通量不好直接判断,便通过感应电流来间接研究.课本上也正是先判断出电流表的指针偏转方向和电流方向间的关系,再通过磁铁和导体棒、螺线管分别作用,使其产生感应电流,由电流表指针偏转进而倒推出感应电流方向,最后,再由右手螺旋定则判断出感应电流的磁场, 并和原磁场比较,总结出感应电流的磁场与引起感应电流的磁场(即原磁场)的关系.最后,通过多次实验后总结出感应电流的磁场总是阻碍引起感应电流的磁通量的变化,即楞次定律.
为此,笔者按以下思路进行探究:先搞清电流方向与灵敏电流计指针偏转方向间的关系,然后,让线圈和磁铁发生相对运动,产生感应电流.再看感应电流导致灵敏电流计指针偏转方向,进而倒推出线圈中感应电流的方向.判断出感应电流的磁场,再根据楞次定律,即感应电流的磁场总是阻碍引起感应电流的磁通量的变化确定线圈内磁通量如何变化.这也是楞次定律的具体应用,且可以加深学生对楞次定律内容的理解.
笔者先带领学生研究例1的情况,用试触法或连接成如图3所示电路进行判断.
当电流从正接线柱流入时,灵敏电流计指针右偏,从负接线柱流入时,灵敏电流计指针左偏.

图3 图4
再将线圈和灵敏电流计连成一个回路(图4),搞清线圈绕向和流入灵敏电流计电流而导致的电流表指针偏转方向的关系(用红、黑两种颜色导线分别接到红、黑接线柱上,即从红色线流入红接线柱经电流表黑接线柱流出而导致灵敏电流计指针右偏).然后研究此时线圈的两面.从正面看去,若有电流应为逆时针方向,则由右手定则可知,感应电流磁场则从背面指向正面,即垂直纸面向外.
开始试验,条形磁铁水平放置,且左侧为N极.将线圈从条形磁铁最左侧套上,移向中间,灵敏电流计指针左偏,电流为顺时针,感应电流的磁场向右,原磁场向左增加,或向右减少,深入分析可知原磁场只能向左,故原磁场向左且在增加.将线圈从条形磁铁中间移向右端,灵敏电流计指针右偏,则电流经过红接线柱流进电流表,线圈电流从正面看为逆时针,故感应电流磁场向左,原磁场向左减少.这与理论解释符合得很好.
有了第一种探究的思路和结论,增加了学生的自信,笔者又带领学生探究例2的情形.将几个条形磁铁并排放于实验桌上,充当题中的扁平条形磁铁,将线圈放于条形磁铁之上,从左端移到中间,灵敏电流计指针右偏,从红色线流入灵敏电流计,故电流从正面看为逆时针,所以,感应电流的磁场向左,又因为原磁场向右,故只能是磁通量增大.将线圈从条形磁铁中间向右移动的过程中,灵敏电流计指针左偏,即电流从黑色线流入灵敏电流计,电流从正面看为顺时针方向,故感应电流磁场方向向右,又因为原磁场方向向右,故磁通量减少.整体看来,当线圈位于条形磁铁上方且从左向右移动的过程中,穿过线圈的磁通量先增大后减少,且中间的磁通量最大.
如此看来,这就和中间磁通量少相矛盾了.如何解释呢?笔者又做了一些理论探究.在图2中,线圈abcd运动方向基本和磁感线在同一面,可近似认为不切割磁感线,而两条与条形磁铁平行的边切割磁感线的竖直分量,如图5所示.
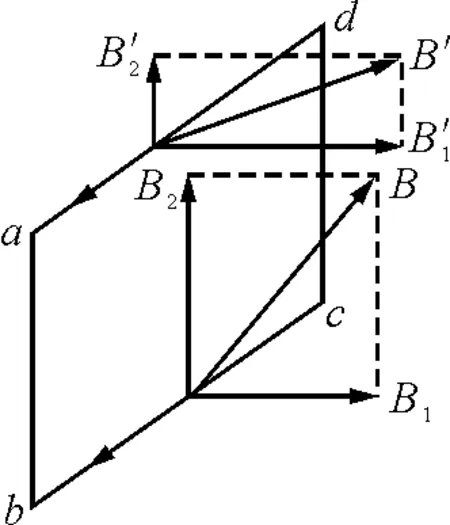
图5
由图5可知,当线圈从条形磁铁左侧移向中间时,ad边向右运动切割磁感线产生的电流方向为从d到a,bc边向右运动切割磁感线产生的感应电流方向从c到d.由图5可知bc边切割产生的感应电流大,故整个线圈感应电流为adcb方向,因此,线圈中感应电流产生的磁场方向水平向左,又因为原磁场方向水平向右,由楞次定律可知,磁通量应增大,同理,当线圈从条形磁铁中间向右移动的过程中,磁通量应减少.
由实验和理论分析可知,两种情况应选用不同的模型来处理.然后,笔者又将学生分组,用此法继续研究磁铁、线圈模型中可能出现的其他情况,如线圈平行条形磁铁从远处靠近或远离磁铁等情况.每组学生有记录、有总结,有发言人.学生兴趣盎然,讨论激烈.最后,汇报时人人充满自信,体验了研究过程和获得成功的快乐.
因此,笔者认为,对于高中物理中有争议的问题,教师应勇敢面对,带领学生去研究.也许因某种情况的制约可能得出错误或不全面的结论,但学生在这一过程中所学到的科学研究方法和过程却可以终身受用.这才是学习的真谛之所在,即重在过程,学会学习,享受学习,并能体会到学习研究之快乐.
参考文献
1 人民教育出版社编辑室.《普通高中课程标准实验教科书》物理3-5.第三版.北京:人民教育出版社,2010
2 陈合森.对一道磁通量习题的证明.中学生数理化.2010

