非线性变折射率大气中的海市蜃楼

张九铸

(金川集团公司龙门学校 甘肃 金昌 737100)

设大气折射率与相对海面的高度y成非线性关系[1]

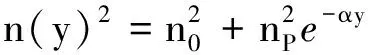
(1)

式中各常数的典型值n0=1.000 233，nP=0.458 36，α=2.303/m．建立坐标系xPy如图1所示，设物点P(0,0)与海平面等高，由于大气折射率的连续变化，物点P向各方向发出的光线将连续向下弯曲，地面上与海平面等高处的观察者眼睛A将接收到很窄的折射光光锥(因为瞳孔很小)，光锥顶点P′就是物点P的像，称为蜃景．由P点射出的光线的仰角φ不同，能看到像P′的人的位置A(x2,0)也将不同．基于式(1)，笔者将利用变分法导出人能够看见蜃景的条件及P,A之间距离的计算式．

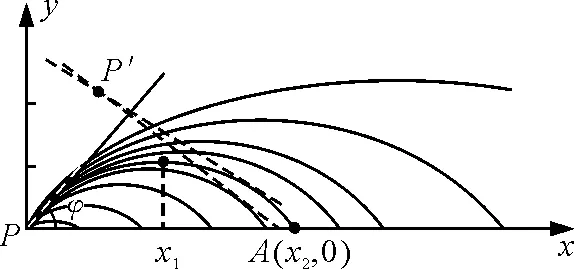
图1

1 光线方程

设由P点发出的一条光线经过某点(x1,y1),则由P到该点的光程为

(2)

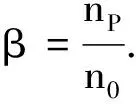
相关偏导数为

而

将以上结果代入欧勒方程

得到

-αβ2e-αy(1+y′2)=2y″(1+β2e-αy)

(3)

由于

代入式(3)并且分离变量，有

积分得到

1+y′2=C1(1+β2e-αy)

(4)

固定边界条件为yx=0=0，y′x=0=tanφ，代入式(4)解得

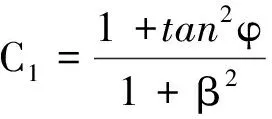
(5)

设0≤x≤x1范围内y′≥0，式(4)可以变为

(6)

其中

a=C1-1b=C1β2

积分式(6)得到[2]

再将固定边界条件yx=0=0代入以上二式，分别解得

于是得到

(7)

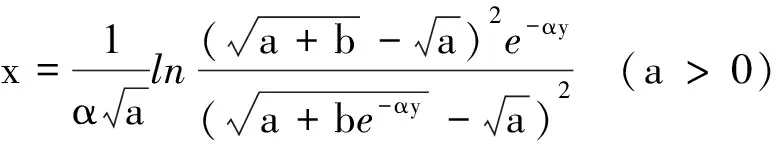
(8)

式(7)、(8)是0≤x≤x1范围内的光线方程．

2 形成蜃景的条件和物点与观察者之间距离

第一种情形：a≥0即C1≥1或tanφ≥β．先将式(4)变为

y′2=(C1-1)+C1β2e-αy=a+be-αy

由此式可见,因为b=C1β2>0，所以a≥0时y′不可能为零．这说明在这种条件下光线不存在最高点，不发生全反射，光线不向下弯曲，人无法在地面上看见蜃景．又由式(5)可知此时有

代入数据得

则

φ≥24.62°

即仰角φ≥24.62°的光线不发生全反射．特别地，对于a=0的情形，此时式(4)变为

y′2=β2e-αy

(9)

可见,此时只有在y→∞处才有y′=0，其实人无法在地面上看见蜃景．

第二种情形：a<0即C1<1或tanφ<β．这种情况下，由式(4)可知光线有最高点，也就是说人在地面上可以看见蜃景.令x=x1时y=y1，y′=0，代入式(4)得

a+be-αy1=0

(10)

再令式(7)中的x=x1，y=y1，并将式(10)代入，得

根据对称性，并且考虑式(5)、(6)，得到P,A之间水平距离为

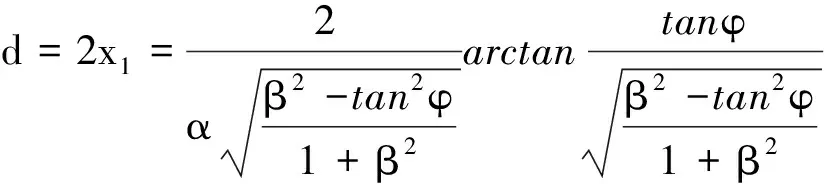
(11)

总之，在大气折射率作如式(1)变化时，只有仰角φ<24.62°的光线才能发生全反射，亦即只有这一区域的光线才能形成海市蜃楼．

参考文献

1 钟锡华．现代光学基础．北京：北京大学出版社，2003.17～18

2 《实用积分表》编委会．实用积分表．合肥：中国科技大学出版社，2006.118