磁场范围的最小面积

邬剑峰

(奉化中学 浙江 宁波 315500)

在平常教学过程中，笔者遇到这样的一道题.

【题目】电子质量为m，电荷量为e，如图1所示，从坐标原点O处沿xOy平面射入第一象限，射入时速度方向不同，速度大小均为v0．现在某一区域加一垂直于xOy平面的匀强磁场，磁感应强度为B，磁场方向垂直纸面向外.若这些电子穿过磁场后都能垂直射到荧光屏MN上，荧光屏与y轴平行.求：

(1)荧光屏上光斑分布的长度；

(2)所加磁场范围的最小面积．

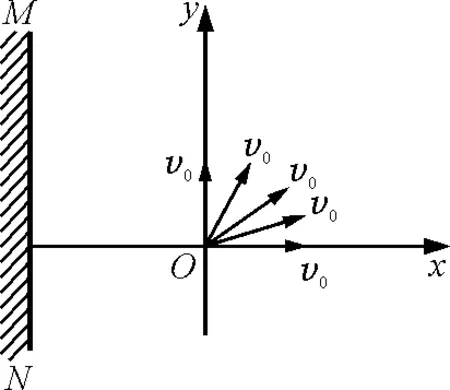
图1

分析：(1)如图2所示，求光斑分布长度，关键是找到两个边界点，初速度方向沿x轴正方向的电子，沿圆弧OB运动到P；初速度方向沿y轴正方向的电子，沿圆弧OC运动到Q．电子在磁场中的半径为

由几何关系可知

图2

(2)沿任一方向射入第一象限的电子经磁场偏转后都能垂直打到荧光屏MN上，所加最小面积的磁场的边界是以O′(0，R)为圆心，R为半径的圆的一部分，如图2中实线所示，所以磁场范围的最小面积

笔者查阅了多本参考书和网上的解答，尽管解答的方法有所不同，但其所加磁场范围的最小面积是跟上面的结论是一样的，笔者认为这个问题还可以进一步探讨．

要弄清这个问题，首先来要了解两个推论(下面讨论的磁场都为匀强磁场，且方向垂直纸面向外)：

(1)如果磁场区域(圆形)的半径R1和电子在该磁场区域的偏转半径R2相等时，那么在磁场边缘O点向各个方面发射的电子经磁场偏转后，电子将沿同一方向运动．如图3(a)所示．(利用电子入射点、磁场区域圆心、电子出射点和电子运动轨迹圆心构成菱形，即可证明此结论)

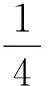
所加磁场的最小范围为一“树叶”形状.

图3

图4

让我们来看另一个推论：如图5所示，在单边界的磁场区域里，通过几何关系可知，如果电子与边界成θ角进入磁场，那么电子一定与边界成θ角离开磁场．

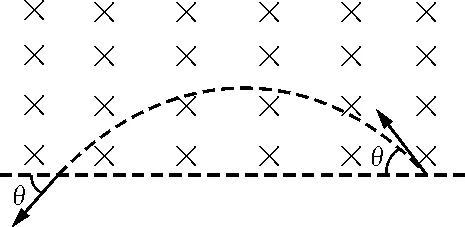
图5

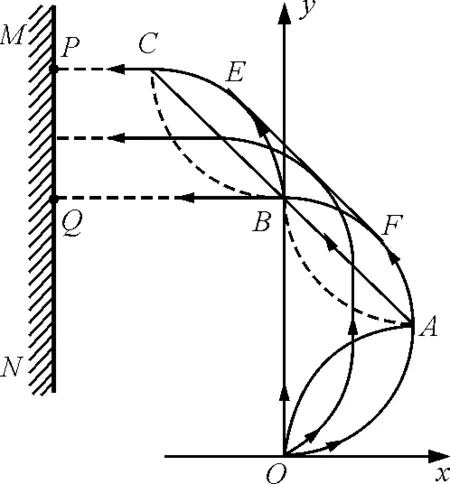
图6

结语：求解磁场区域的最小面积一般从找出边界点或边界线入手，然后再确定区域形状，最后利用几何关系求出相应面积，如果题目没有特殊的要求，可以通过“割补”把整个区域进行分解，以求得最小面积．