基于ITD法的结构模态参数识别

狄生奎， 张得强， 李 健

(兰州理工大学 土木工程学院， 甘肃 兰州 730050)

建筑结构在正常的使用过程中由于地震等自然灾害原因会产生不同程度的损伤。这种损伤会使得整个结构的整体承载能力下降，导致结构破坏，因此如何正确的诊断和评价这些建筑结构尤其是中小学建筑[1]的损伤状态，是结构健康检测领域面临的一个主要问题。许多学者根据不同的结构特征值对结构整体损伤问题进行了研究，其中有Sozen提出的层间位移角指标[2]；李国强等利用结构的前几阶动力模态提出的框架结构损伤识别的两步法[3]；Ghobarah提出的结构遭遇地震前后的刚度比指标[4]；韩建平教授对基于振动台试验框架结构的模型修正[5]及固有频率识别方法的对比进行了研究[6]；钟军军等针对有损结构前几阶固有频率和对应的模态位移可供利用的情况，提出了一种基于广义逆的损伤识别方法[7]。模拟地震振动台模型试验是研究结构模态参数的重要手段之一，可对结构在不同水平地震动激励下反应性态及破坏提供直接可观的结果。本文将用一种模态参数时域识别方法——ITD法来识别振动台模型试验结构的频率、阻尼比和振型系数等模态参数。

1 ITD法的理论依据

ITD法的基本思想是以粘性阻尼线性系统多自由度系统的自由衰减响应可以表示为其各阶模态的组合理论为基础，根据测得的自由衰减响应信号进行三次不同延时采样的采样，构造自由响应采集数据的增广矩阵，即自由衰减响应数据矩阵，并由响应与特征值之间的复指数关系，建立特征矩阵的数学模型，求解特征值问题，得到数据模型的特征值和特征向量，再根据模型特征值与振动系统特征值的关系，求解系统模态参数[8]。

利用结构的自由振动反应的表达式：

(1)

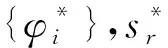
k时刻i测点的结构自由振动反应为：

(2)

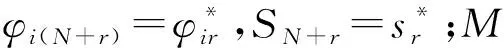
假设共有m个实测点，为了使测点数等于2倍结构自由度数，采用延时方法由实测点构造虚测点。令延时可取采样时间间隔为1倍，则虚测点的自由振动响应可以表示为

(3)

这样得到由实际测点和虚拟测点组成的M个测点在L个时刻的自由振动响应值所建立的响应矩阵：

(4)

或简写成：

从某种意义上说，基于ICT的成人参与学习本质是有效使用ICT，是人们发展与ICT的关系以及能够获得有用的教育资源。在思考ICT对成人参与学习的价值时，既不能以“技术决定论”为导向过分夸大ICT技术在教育与社会发展中的角色，亦不可以“社会决定论”为导向仅赋予ICT为中性技术工具的内涵，而误解其所涵盖的社会文化特性［17］。因此，如何面对使用ICT过程中所产生的来自心理、教育、社会等复杂因素交织而成的障碍，学习个体、教育机构、决策组织乃至关联企业的应对之策，均至关重要。

[X]M×L=[φ]M×M[Λ]M×L

(5)

将包括虚拟测点在内的每一测点延时Δt，则由式(1)可知

(6)

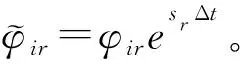
由M个测点在L个时刻的响应所构成延时Δt的响应矩阵可表示为

(7)

式中：[α]为对角矩阵。[α]对角线上的元素为

αr=esrΔt

(8)

经过整理后得到

[A][φ]=[φ][α]

(9)

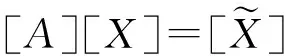
(10)

Rr=lnVr=srΔt

(11)

(12)

(13)

为了减小测试噪声的影响，提高阻尼比的识别精度，计算矩阵[A]可采用双最小二乘解的方法。该方法是取两种单最小二乘解的平均值作为识别模态参数的特征矩阵[A]，即

[A]=

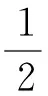
(14)

2 结构模型试验

用该方法对一个钢筋混凝土框架结构振动台试验模型的模态参数进行了识别研究。该模型由同济大学土木工程防灾国家重点实验室振动台试验室完成，模型共12层，模型比例为1/10，具体传感器位置见图1，试验中的激励波形为EI Centro波、 Kobe波、上海人工波和上海基岩波。在每次输入的加速度值改变之前都先输入白噪声波以观察模型的动力特性。整个试验共分为62个工况，其中8次白噪声输入，28次X方向的单向地震波输入，14次XY向的双方向地震波输入，12 次XYZ三向地震波输入。有限元模型分析时先进行自重荷载分析和模态分析，然后按照振动台试验时的工况进行有限元模型的非线性时程分析。其他更为详细的资料可以参考研究报告[9，10]。

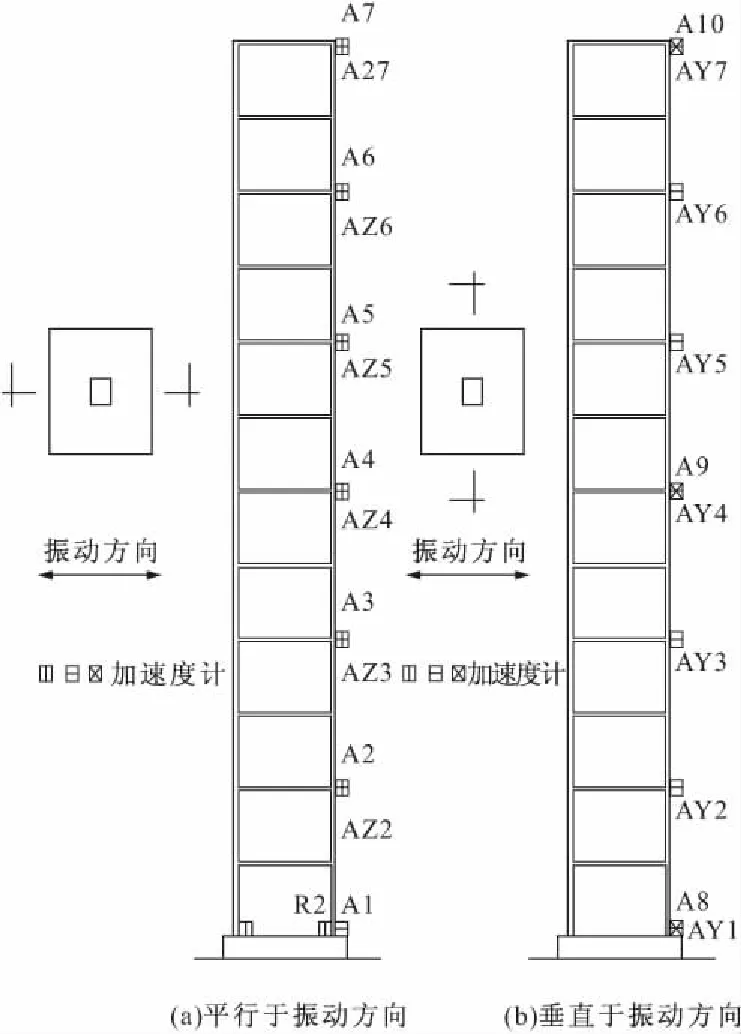
图1 模型尺寸及测点布置

3 模态参数识别

本试验62个工况每个工况测得33组数据，由于文章篇幅有限不能全部列出，本文仅以在振动台模型试验中放置在第8层的传感器所测得数据为例说明。先将试验数据经过傅立叶变换(如图2)，再利用随机减量法对试验模型的输出数据进行预处理，然后用ITD法分析出频率、阻尼比及振型系数，本文中振型系数是指在结构某一阶模态频率下某个质点的相对位移。结果如表1所示。

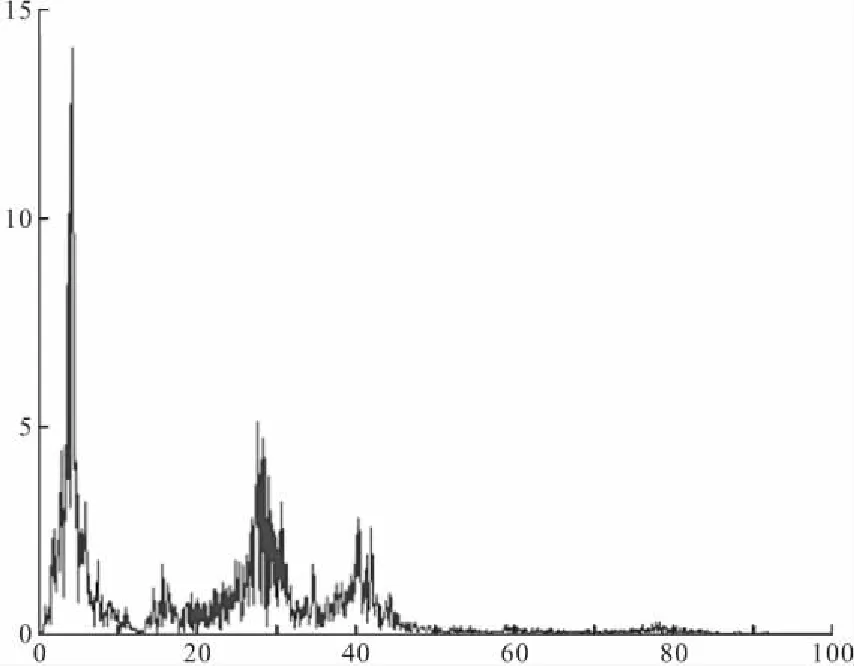
图2 第2工况响应的傅立叶变化结果

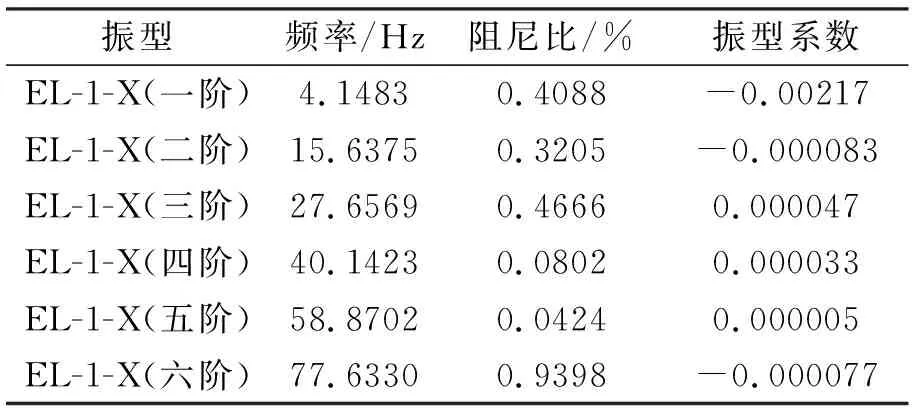
振型频率/Hz阻尼比/%振型系数EL-1-X(一阶)4.14830.4088-0.00217EL-1-X(二阶)15.63750.3205-0.000083EL-1-X(三阶)27.65690.46660.000047EL-1-X(四阶)40.14230.08020.000033EL-1-X(五阶)58.87020.04240.000005EL-1-X(六阶)77.63300.9398-0.000077

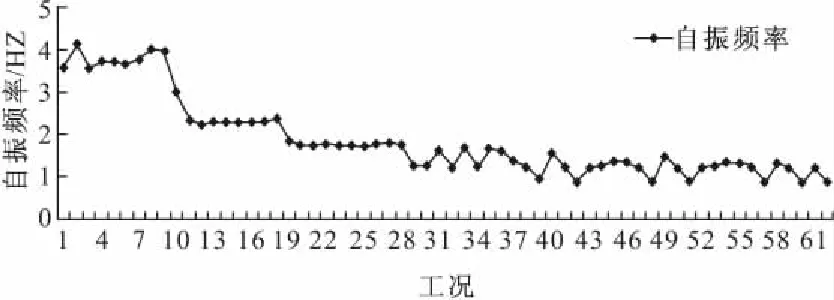
图3 结构自振频率变化

为了得到模型结构受到损伤后的动力特性,本文对振动台试验所有工况的输出数据进行了分析并运用有限元软件对结构模型进行了非线性时程分析。从图3中可以看出振动台模型结构的自振频率在试验过程中随着加速度值不断增大的地震波的输入下降比较明显，呈阶梯形变化。第二阶梯形变化处的第9工况自振频率相比第2工况由4.1483 Hz降到2.9828 Hz(下降了28.10%)，实际模型试验第9工况后在4层平行于X振动方向的框架梁的梁端首先出现细微的自上而下和自下而上发展的垂直裂缝，其中两阶的振型变化如图4所示；在第三阶梯处的第18工况的自振频率相比第2工况由4.1483 Hz降到 1.8293 Hz(下降了55.90%)，实际模型试验第18工况后在平行于X振动方向的3～6层框架梁的梁端有垂直裂缝贯通，最大裂缝宽度在第4层处，其中两阶的振型变化如图5所示。第27工况之后的结构自振频率呈现波动状态，第27工况(PGA=0.517g)与第2工况(PGA=0.090g)前四阶振型变化结果如图6所示，第一阶振型变化较大，后面三阶也有不同程度的变化。这说明振动台框架模型的结构动力特性已经发生了比较明显的改变，其结构已经受到严重损伤。

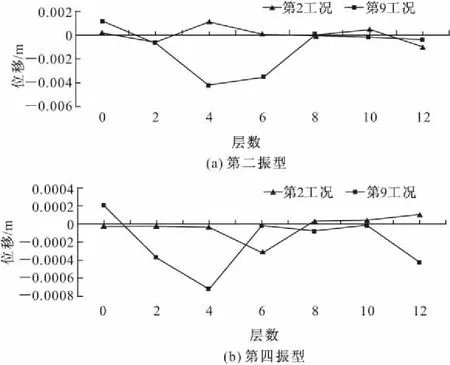
图4 第2工况与第9工况的振型比较

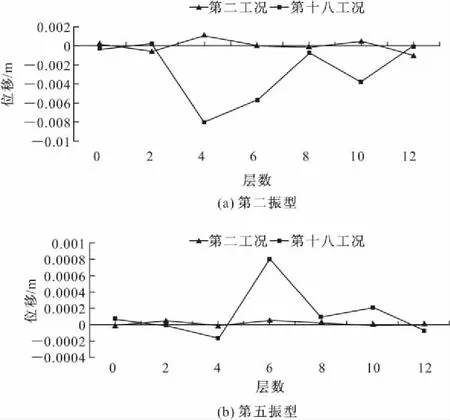
图5 第2工况与第18工况的振型比较

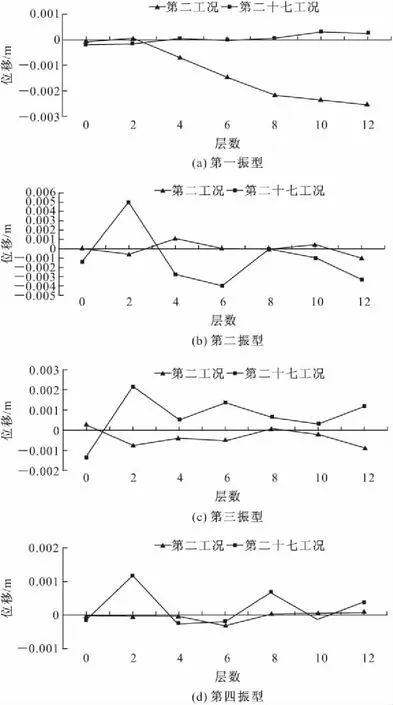
图6 第2工况与第27工况的振型比较

图7为对试验数据分析出来的阻尼比结果，以第2工况为例，从图中可以看出数据的波动比较大。

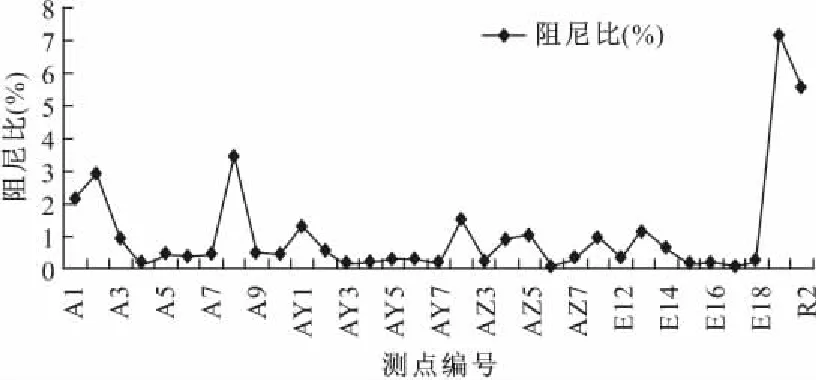
图7 第2工况阻尼比(%)识别结果

4 有限元分析

在通用有限元软件SAP2000中按照振动台试验模型的原型建模，即12层单跨框架结构，高宽比为6，层高为3 m，开间和进深均为6 m，柱截面为500 mm×600 mm，梁截面为300 mm×600 mm，楼板厚度为120 mm，材料采用C30砼。有限元软件SAP2000中材料属性按照规范定义，楼板采用膜结构模型，非线性分析的时程类型采用直接积分法。

按照振动台试验时的工况顺序和输入地震波的参数在有限元软件SAP2000中对该计算模型进行了非线性时程分析。模拟结果发现随着输入地震波加速度值的增大，结构的各层水平位移均在增大，顶层最为明显，结构各层的层间位移和层间位移角也在增大。通过对所有工况结果的分析可知该结构的最大层间位移和最大层间位移角主要集中在第3～6层之间，如图8所示。该计算模型的最大层间位移和最大层间位移角对不同的地震波作用敏感程度不同。对于上海人工波，由于占有相当能量比例的优势频率与第6层最大层间位移角相应振形所对应的高阶频率相近，该层层间位移角响应很明显；对于El Centro波，由于占有相当能量比例的优势频率与第5层最大层间位移角相应振形所对应的高阶频率相近，该层层间位移角响应比较明显。

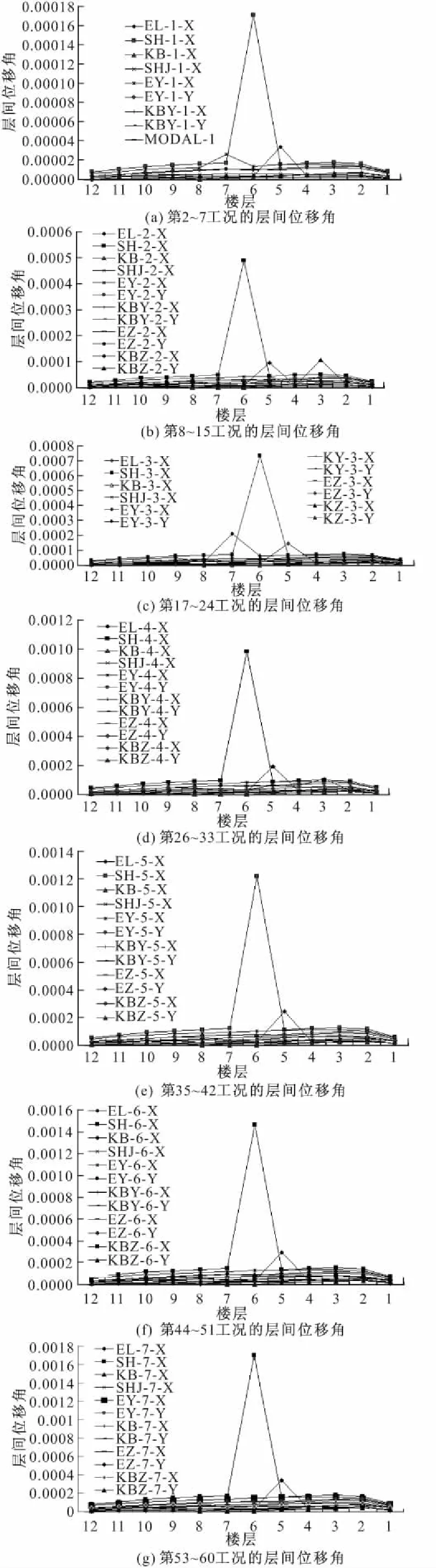
图8 各工况层间位移角

5 结 论

(1)该框架在第3～6层为薄弱位置，该类框架结构在今后抗震设计中此部分应该加强处理。

(2)振动台模型结构的自振频率在随着加速度值不断增加的地震波的输入下呈阶梯形下降，第3阶梯处的频率仅为第1阶梯处的44.10%，第27工况之后结构自振频率呈现波动状态，各工况的振型随着结构自振频率的下降也有改变，主要集中在3～6层，而第27工况的振型与第2工况的振型相比有明显的变化，说明在模型结构中已经有塑性铰的形成，结构的动力特性发生了比较明显的变化，结构已受到了严重的破坏。

(3)用ITD法对振动台试验有关阻尼比的分析结果呈现波动状，对阻尼比的分析不够精确。

[1] 聂肃非,李 黎,孙 明,等. 武汉市主城区中小学建筑物震害及人员伤亡预测[J].华中科技大学学报(城市科学版)，2010，27(4): 97-99.

[2] Sozen M A. Review of Earthquake Response of Reinforced Concrete Buildings with a View to Drift Control [C] //State of the Art in Earthquake Engineering, 7th World Conference on Earthquake Engineering. Istanbul , 1980: 119-174.

[3] 李国强, 郝坤超, 陆 烨. 框架结构损伤识别的两步法[J]. 同济大学学报(自然科学版),1998,26(5): 483-487.

[4] Ghobarah A,Abou-Elfath H,Ashraf Biddah. Response-based damage assessment of structures [J]. Earthquake Engineering and Structural Dynamics, 1999,28(1) :79-104.

[5] 韩建平,董小军,周 伟. 基于振动台实验的RC框架模型修正及模拟损伤识别[J].地震工程与工程震动,2010,30(5):87-92.

[6] 韩建平,王飞行,李 慧. 基于振动台试验的模态参数识别算法比较研究[J].华中科技大学学报(城市科学版),2008,25(3):57-60.

[7] 钟军军,董 聪,夏开全. 基于频率及振型参数的结构损伤识别方法[J].华中科技大学学报(城市科学版),2009,26(4):1-5.

[8] 王 济,胡 晓. MATLAB在振动信号处理中的应用[M].北京:中国水利水电出版社,2006.

[9] 吕西林,李培振,陈跃庆.12层钢筋混凝土标准框架振动台模型试验的完整数据[R].上海: 同济大学土木工程防灾国家重点实验室,2004.

[10] 公茂盛,谢礼立,欧进萍. 结构振动台模型模态参数识别新方法研究[J].振动工程学报,2010,23(2)：230-236.