基于蒙特卡罗数值模拟的桥梁可靠度分析

符 蓉, 叶 昆, 宗 昕, 张子翔， 程志远

(1.华中科技大学文华学院城建学部， 湖北 武汉 430074；2.华中科技大学 a.土木工程与力学学院; b.控制结构湖北省重点实验室， 湖北 武汉 430074；3.中交第二公路勘察设计研究院有限公司, 湖北 武汉 430056)

根据公路结构可靠度设计的统一标准[1]，概率理论已经被引进，极限状态的概率设计已经被指定为结构设计的一般原则，这在结构设计理论上是一个突破。但是，在状况评估领域，特别是在大跨度桥梁的状况评估领域，还没有完美的理论可以把那些不确定因素很准确地考虑进去[2～4]，所以那些不确定的因素所造成的影响很难分析。至今为止，大部分的分析依靠专家的定性估计，但是，对于那些从事桥梁日常养护的人来说，通过这些不确定和模糊的描述做出快速、准确的判断是很困难的。

为了定量考虑任意因素造成的影响，以及为桥梁的安全检测和状况评估提供一个可靠的依据，在以下的研究中，我们用基于蒙特卡罗模拟的概率分析对桥梁在各种因素下的可靠度进行分析。

1 蒙特卡罗数值模拟

1.1 基本原理

蒙特卡罗方法的实质是通过大量的随机试验，利用概率论解决问题的一种数值方法，基本思想 是基于概率和体积间的相似性[5]。蒙特卡罗法是通过抽样统计原理建立一个数学或物理模型，从而解决实际问题。通常，首先提出一个与实际问题有着某种联系的概率模型，然后用计算机按照指定的分布，产生足够的输入变量的值，这意味着已经做好了足够的实验，因为模型和实际问题之间有相似之处，这些生成的数值就可以模拟实际问题中随机因素的变化，最后，这个模型的计算特征值(即输出变量的值或标准偏差等)可以为实际问题提供一个近似解决方案。

1.2 基于直接抽样的蒙特卡罗模拟

直接通过随机抽样对结构的可靠度进行模拟，是结构可靠度蒙特卡罗模拟的最基本方法，可称为直接抽样法[6]。

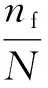
(1)

结构失效概率为：

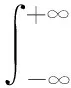
(2)

式中，I(x)为x的指示函数(或称特征函数、示性函数)，规定当x<0时为I(x)=1，x≥0时为I(x)=0。I[gx(x)]在此将积分区域从规则的失效域Ωf扩充至无穷大规则域，使被积函数在整个gx(x)≥0的区域为零。

根据式(2)，设X的第i个样本值为xi，则Pf的估计值为：

(3)

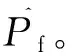
(4)

(5)

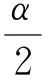
(6)

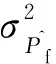
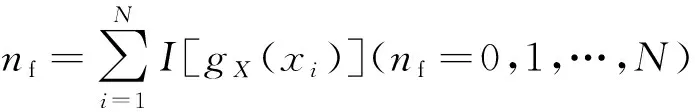
(7)

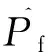
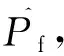
2 基于蒙特卡罗法的桥梁可靠度分析

2.1 计算原理

结构可靠度是指在规定的时间内、规定的条件下，完成预定功能的概率[8]。

设X=(X1,X2,…,Xn)T是影响结构功能的n个随机变量，X可以是结构的几何尺寸、材料的物理力学参数、结构所受的作用，机构抗力等。称随机函数Z=g(X)=g(X1,X2,…,Xn)为结构的功能函数(或失效函数)。规定Z>0表示结构处于可靠状态，表示结构处于失效状态。结构可靠度分析就是通过考虑各种随机因素对结构功能的影响，进而确定结构或结构某一部分的失效概率Pf。

《公路工程结构可靠度设计统一标准》中已经给出桥梁结构中荷载，荷载效应，抗力等参数的概率分布，实际工程中还可根据工程实际情况加以修正。运用蒙特卡罗法对桥梁进行可靠度分析的步骤如下：

(1)根据预先规定的失效准则写出桥梁各截面的功能函数Z=g(X)=g(X1,X2，…,Xn)；

(2)根据桥梁规范以及实测确定功能函数中各随机变量的概率分布；

(3)按照各随机变量的概率分布采用一定的抽样方法分别生成各变量的随机数，每次抽样都能生成一组(Xi1,Xi2,…,Xin)T；

(4)根据(1)步骤计算出第i次抽样时功能函数Zi的具体值，共生成N组；

(5)统计出功能函数Zi<0出现的次数，最终得出桥梁各截面的失效概率Pf=Nf/N。

2.2 工程背景

本文以北盘江预应力混凝土悬浇空腹(斜腿)式连续刚构桥为研究背景，主桥桥型布置如图1所示，有限元模型如图2所示。主桥部分总长为895 m，桥跨布置为(82.5+220+290+ 220+82.5) m。上部结构采用连续变截面现浇混凝土箱梁，宽度为10.5 m，由钢筋混凝土桥墩支撑，主墩的高度分别为75 m、90 m、143 m、68 m，均采用双肢薄壁空心截面，其中中间两对桥墩设有空腹斜腿以提高根部刚度。桥台部分的支撑类型为简支。桥墩的纵向配筋主要采用直径32 mm，28 mm，20 mm的HRB335钢筋，横向箍筋为直径为16 mm和20 mm的HRB335钢筋。

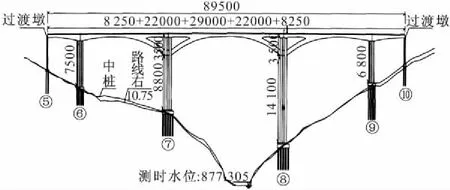
图1 主桥桥型布置/cm

图2 主桥有限元模型/cm

2.3 桥梁各截面失效准则

根据有关规范[9]，取各截面抗弯失效准则如下：

(9)

其中，R为截面极限承载力；γ0为结构重要性系数，这里取1.1；SGd为自重荷载及二期荷载效应设计值；SQd为汽车荷载效应的设计值；SQjd为除汽车荷载效应外的其他第j个可变作用效应的分项系数；ψc为当除汽车荷载效应之外，仍有两个可变作用效应时，取0.70，当仍有三种可变效应时，取0.60，有四种及四种以上可变效应时，取0.50。

2.4 桥梁各截面的功能函数

考虑到桥梁是变截面桥梁，且预应力钢筋形状复杂，直接得出各截面的荷载与荷载效应之间的关系有困难，所以我们采用的方法是运用MIDAS 2010对各种荷载单独作用情况下的荷载效应值进行分析，再不断变换该荷载的荷载值，得出不同荷载值对应的荷载效应值，运用MATLAB的统计工具箱进行线性拟合，得出各种荷载与荷载效应之间的线性关系，进而可求出各截面的功能函数。图3给出的是中跨跨中截面自重系数(MIDAS中的自重系数为G/Gk)和弯矩效应之间的关系。

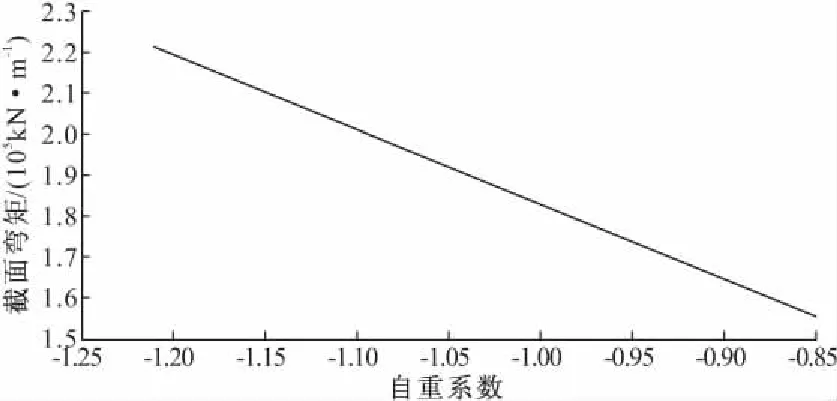
图3 自重系数和截面弯矩之间的线性关系

根据《公路工程结构可靠度设计统一标准》的有关规定，并综合考虑北盘江大桥的实际情况，取截面抗力概率分布如表1所示。现取各荷载与荷载效应的概率分布如表2而所示。

表1 北盘江大桥截面抗力概率分布

2.5 桥梁各截面的可靠度

通过蒙特卡罗随机抽样106次，并记录功能函数大于0的次数，就可以得到北盘江大桥各截面的可靠度，如图4所示。可知，北盘江大桥主桥各跨跨中截面的可靠度相对较低，支座截面处的可靠概率相对较高；全桥最低可靠度在主桥中跨的跨中截面处，可靠度约为0.9968。

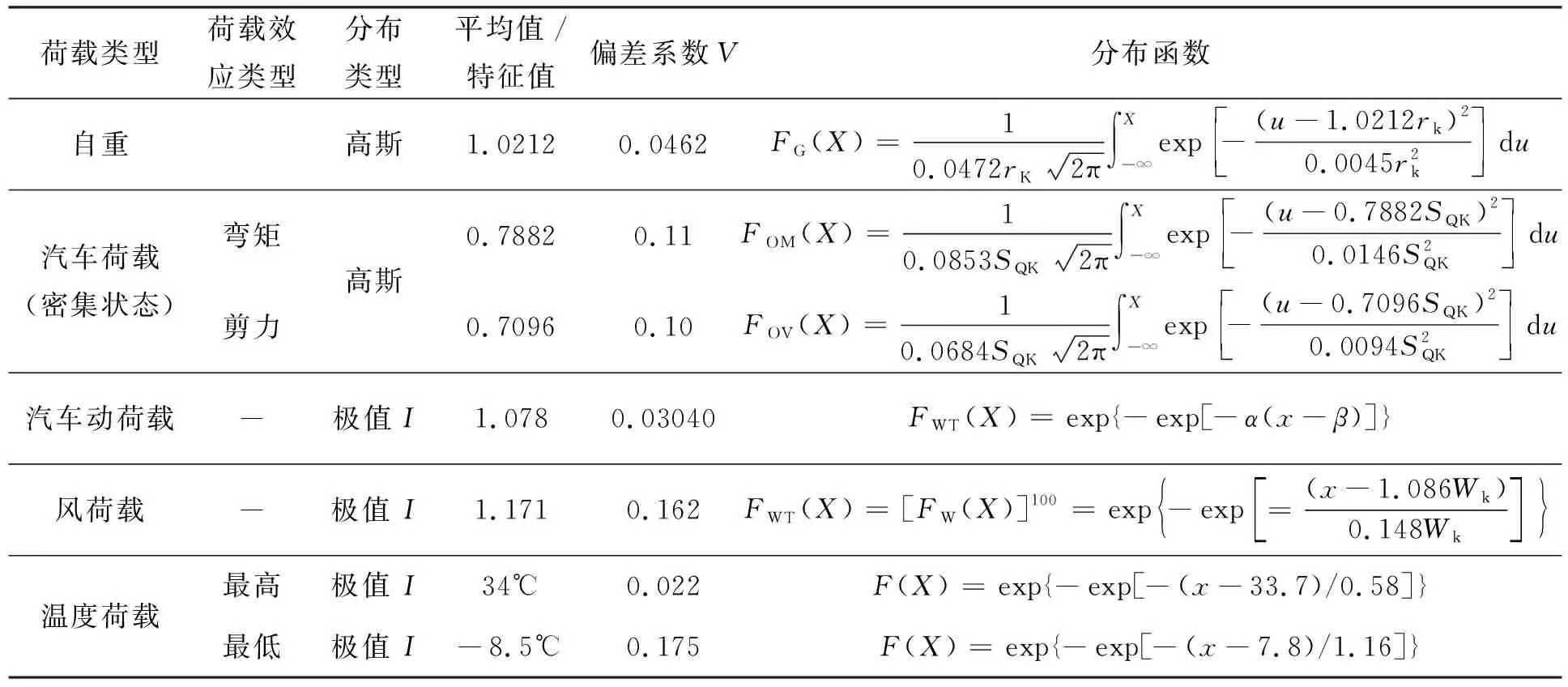
表2 北盘江大桥荷载及荷载效应概率分布

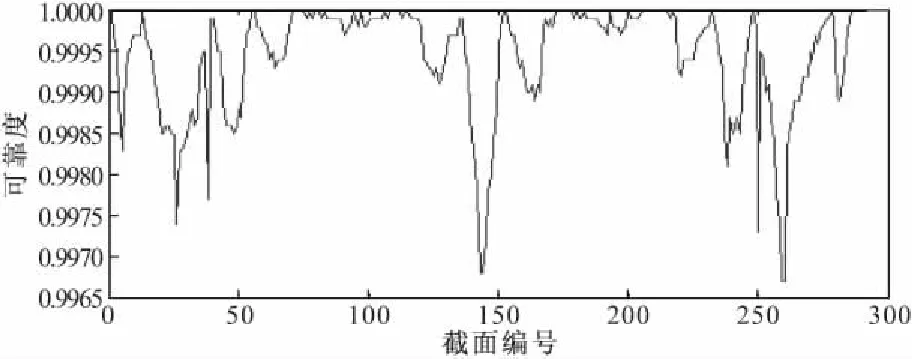
图4 北盘江大桥各验算截面可靠度

3 结 语

如果抽样次数足够多的话，蒙特卡罗法可以被认为是一种精确的方法。在桥梁正常运营阶段，通过对实测监控数据的搜集和分析，可以不断的升级评价项目，得到更为精确的结果。通过本文介绍的蒙特卡罗数值模拟方法，可以定量分析各随机变量对桥梁结构的影响，并且结果也可以以一种直观清晰的方式表示出来，因此，我们对桥梁结构的维护决策也可以变得更加准确而且目的性更强。

[1] GB/T 50283-1999,公路工程结构可靠度设计统一标准[S].

[2] Guo Tong, Li Aiqun, Miao Changqing. Monte Carlo numerical simulation and its application in probability analysis of long span bridges[J].Journal of Southeast University(English Edition)，2005,21(4):469-473.

[3] Rens Kevin L, Nogueira Carnot L, Transue David J. Bridge management and nondestructive evaluation[J].Journal of Performance of Constructed Facilities,2005,19(1):3-16.

[4] Wong K Y, Chan W Y K, Man K L. The use of structural health monitoring system in operation & maintenance of cable supported bridges[C]//One Day Annual Seminar Structural Symposium 2000 Highway and Railway Structures. Hong Kong, 2000:108-133.

[5] 张建仁,刘 扬,许福友.结构可靠度理论及其在桥梁工程中的应用[M].北京：人民交通出版社, 2003．

[6] 金勇进. 抽样：理论与应用[M].北京：高等教育出版社，2009.

[7] 董 聪，夏人伟.现代结构系统可靠性评估理论研究进展[J].力学进展, 1995，25(4)：537-548．

[8] 黄兴华.浅谈桥梁可靠度计算方法[J].中国水运，2010，10(2)：135-136．

[9] JTG D60-2004，公路桥涵设计通用规范 [S].