大尺度水下综合试验模型拖曳运动特性研究

，，

(1.中国船舶科学研究中心，江苏 无锡 214082；2.清华大学 航天航空学院，北京 100084)

目前，开展水下航行体破损、大攻角、水下拖曳等非正常工况下或应急工况下的运动特性研究时[1-4]，小尺度模型的尺度效应难以克服，出于安全考虑，实船试验也难以进行。鉴于特殊工况下水下航行体的运动特性的复杂性和影响因素多等原因，除依靠理论计算分析之外，大尺度模型试验也是重要的研究手段；此外，理论计算结果也需要经过大尺度模型试验的验证与修正。因此，大尺度水下综合试验模型成为水下航行体特殊工况下运动特性研究的重要手段之一。

本文主要研究大尺度水下综合试验模型拖曳运动特性。大尺度水下综合试验模型总长25 m，最大设计航速4 m/s，具备自航能力。试验水域为一露天水池，模型的最大行程200 m，其中加速段长70 m，匀速试验段长80 m，减速段长50 m。受试验水域的限制，模型无法通过自身推进器在较短的距离内完成加减速过程，因此考虑采用如图1所示的缆绳牵引方式完成模型的加减速运动过程。

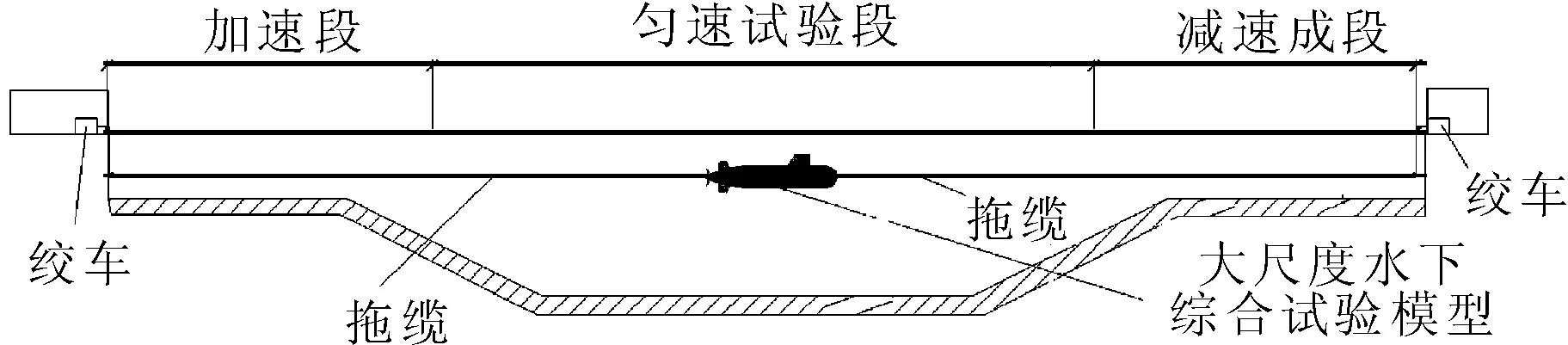
图1 试验模型工作方式示意

拖缆拖曳的试验模型受到外力扰动时，可能会产生运动的振荡发散，影响试验。尤其是铅垂面内的扰动可能会造成模型较大的垂向位移和较大的纵倾，导致模型触底。本文通过数值计算，总结规律，选择合适的预紧力避免模型运动发生振荡发散；对操舵试验的两种典型工况进行计算分析，给出保证试验过程中的运动稳定性和安全性的操舵限制条件。

1 计算模型

试验模型与拖缆组成了一个三维空间的连续弹性振动体系统。由于系统在铅垂面内的运动和在水平面内的运动具有相似性，并且铅垂面内的运动关系到试验模型的安全，因此分析系统铅垂面内的运动意义重大。将系统简化为铅垂面内的二维系统。根据经验估算，试验模型拖缆的直径不大于25 mm，拖缆的总重量不大于1 t，而试验模型的全排水量为210 t，显然试验模型可作为系统中的集中质量处理，将系统简化为弦-集中质量振动体系统。

选用具有零浮力特性的非金属缆绳作为拖缆，考虑到非金属拖缆抗弯刚度很小而抗拉刚度大，近似认为在拖缆中只产生拉力，不产生推力和弯矩；试验模型的刚度远大于拖缆的刚度，故将模型视为刚体，据此将系统进一步简化成如图2所示的弹性体-质量块系统。

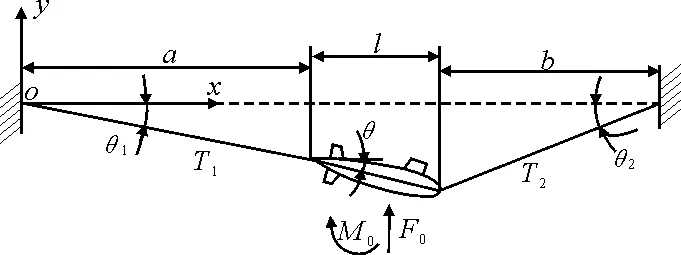
l-模型长度；a、b-模型左、右端缆长

图2中的平面运动系统有纵摇、垂荡和纵荡3种运动模式，用3个独立的参数描述模型的状态。在如图2所示的固定坐标系中，试验模型的状态由坐标(x，y，θ)惟一确定。

由于模型做小振幅运动，θ、θ1、θ2是小量，近似认为sinθ≈tanθ≈θ，sinθ1≈tanθ1≈θ1，sinθ2≈tanθ2≈θ2。近似有

(1)

由于将模型简化为刚体，因此外界的任何扰动都可等效为通过重心的一对合力与合力矩，则试验模型的垂荡运动方程为

θ1+T2θ2+zθ·θ=F0

(2)

式中：m——模型质量；

y——模型重心垂向位移；

C1——水动力引起的垂荡运动阻尼；

T1、T2——模型左右端缆绳张紧力；

zθ——前向运动的水动力修正系数,通过模型试验数据库预报；

θ——模型纵倾角；

F0——外激励力。

试验模型纵摇运动方程为

θ-θ1)+

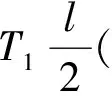
(3)

式中：J——试验模型的转动惯量；

C2——水动力引起的纵摇运动阻尼；

Mθ——纵摇运动的水动力修正系数，通过模型试验数据库预报得出；

M0——外激励力矩。

模型纵向振动对其运动安全性影响不大，可忽略纵向振动，仅考虑前向运动，则模型的水平运动方程为

式中：v——模型的前向运动速度。

将θ1、θ2代入式(2)、(3)，经整理得到模型的运动方程。

2 系统固有特性计算

系统的3个自由度分别对应纵荡运动率、垂荡运动率和纵摇运动固有频率。对本系统而言，只需关心其垂荡运动与纵摇运动特性。当系统的质量特性与阻尼特性一定时，影响系统固有特性的量只有预紧力T。计算不同预紧力作用下，模型从左至右运动时的固有频率特性，结果见图3。

图3 不同预紧力作用下的系统固有频率

由图3可见，模型所处的位置相同时，拖缆预紧力越大，系统刚度越大，其固有频率越高。系统固有频率变化规律与弹性体-质量块振动系统的一般规律是相吻合的。可以认为本文对系统所作的简化是合理可信的。模型左右运动时，垂荡运动及纵摇运动固有频率都随之变化，变化曲线左右不对称，这是因为垂荡运动方程的修正系数zθ导致刚度矩阵不对称，由此可见系统前向运动对系统固有特性的影响不可忽视，见图4。

图4 典型状态下系统的固有特性变化趋势

由图4可见，模型水平运动对纵摇固有频率的影响很小，而对垂荡运动影响较大。当试验模型处于水池中央时，其固有特性具有典型性，可将

此作为一个典型状态，计算不同预紧力作用下系统的固有特性变化规律。从图4可以看出，系统的固有频率都随拖缆预紧力的增大而增大，呈近似线性的关系变化。当拖缆的预紧力T在10～100 kN范围内变化时，系统的垂荡固有频率在0.005～0.016 Hz范围内变化，纵摇固有周期在0.062～0.097 Hz范围内变化。

3 预紧力影响与分析

假定系统在运动初始时刻受到某一未知外力的干扰，产生某一初始偏差，计算系统在不同预紧力作用下的系统响应。仍以4 m/s向前运动的典型工况为例，假定四种典型的初始状态：①初始重心位移0.1 m；②初始垂向速度0.1 m/s；③初始纵倾角1°；④初始纵摇角速度1 °/s。计算不同预紧力作用下的重心垂向位移和纵倾角响应，结果见图5～8。

图5 初始位移为0.1 m时系统的运动响应

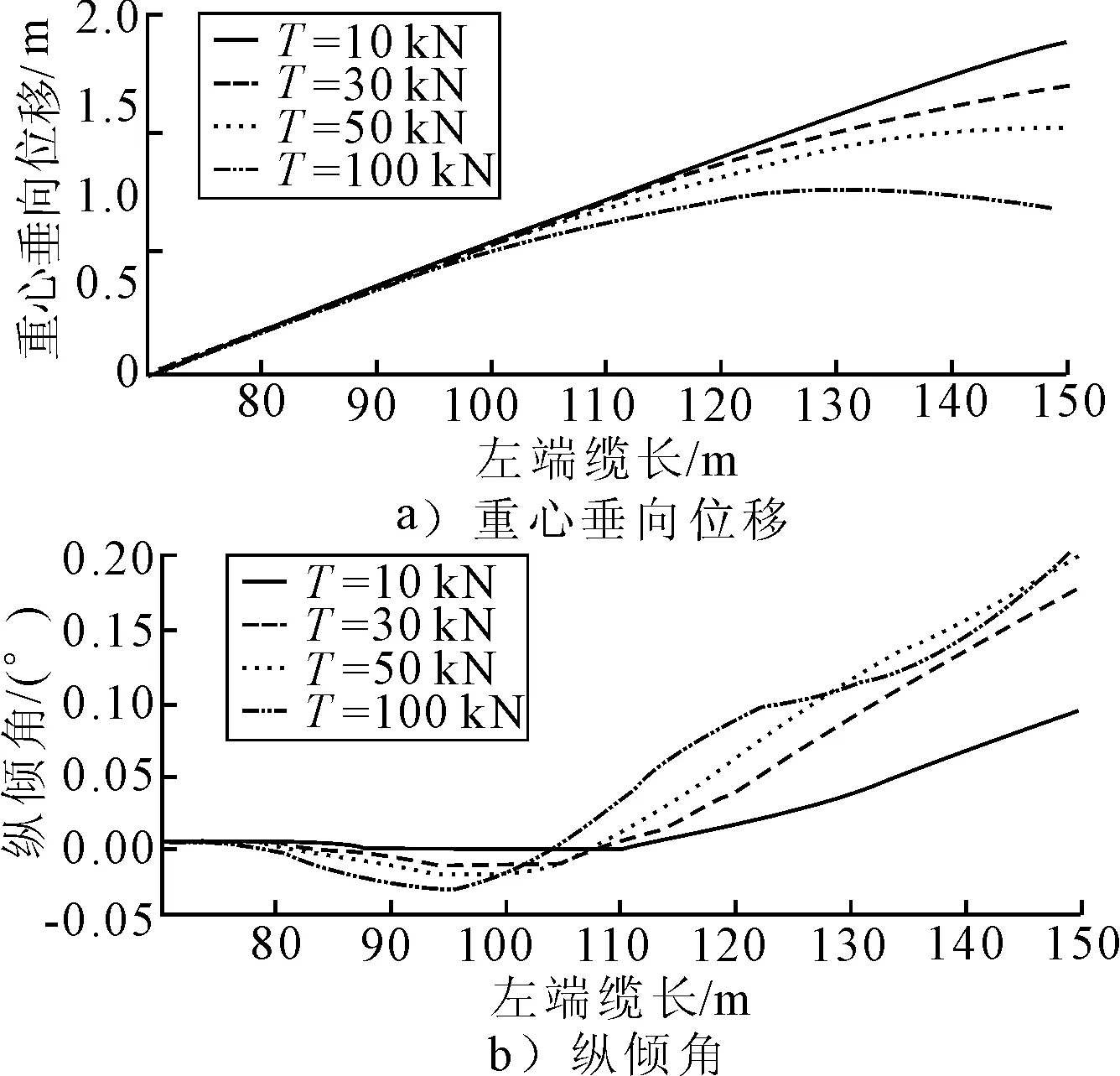
图6 初始垂向速度为0.1 m/s时系统的运动响应

从计算结果可以看出，模型垂荡运动与纵摇运动之间的耦合度很小，即初始重心位移、初始垂荡速度不会造成较大的纵摇响应；初始纵倾、初始纵摇角速度会造成微小的垂荡响应，但绝对值不是很大。预紧力越大，重心、纵倾角的最大超调量越小，重心、纵倾角向初始位置收敛的速度越快，但纵倾角呈现一定的振荡。究其原因，当预紧力T在10～100 kN范围内变化时，垂荡固有周与纵摇固有周期分别在约60～200 s、10～20 s范围内变化，运动时间与纵摇固有周期在同一量级，因此纵倾呈现振荡。过小的预紧力会使得系统的刚度较小，模型偏离初始位置的距离太大，过大的预紧力则会导致纵倾角的振荡，造成运动不平稳。因此拖缆预紧力的选取应考虑使得模型在匀速试验段内尽量平稳运行，且不至于产生过大的超调量。

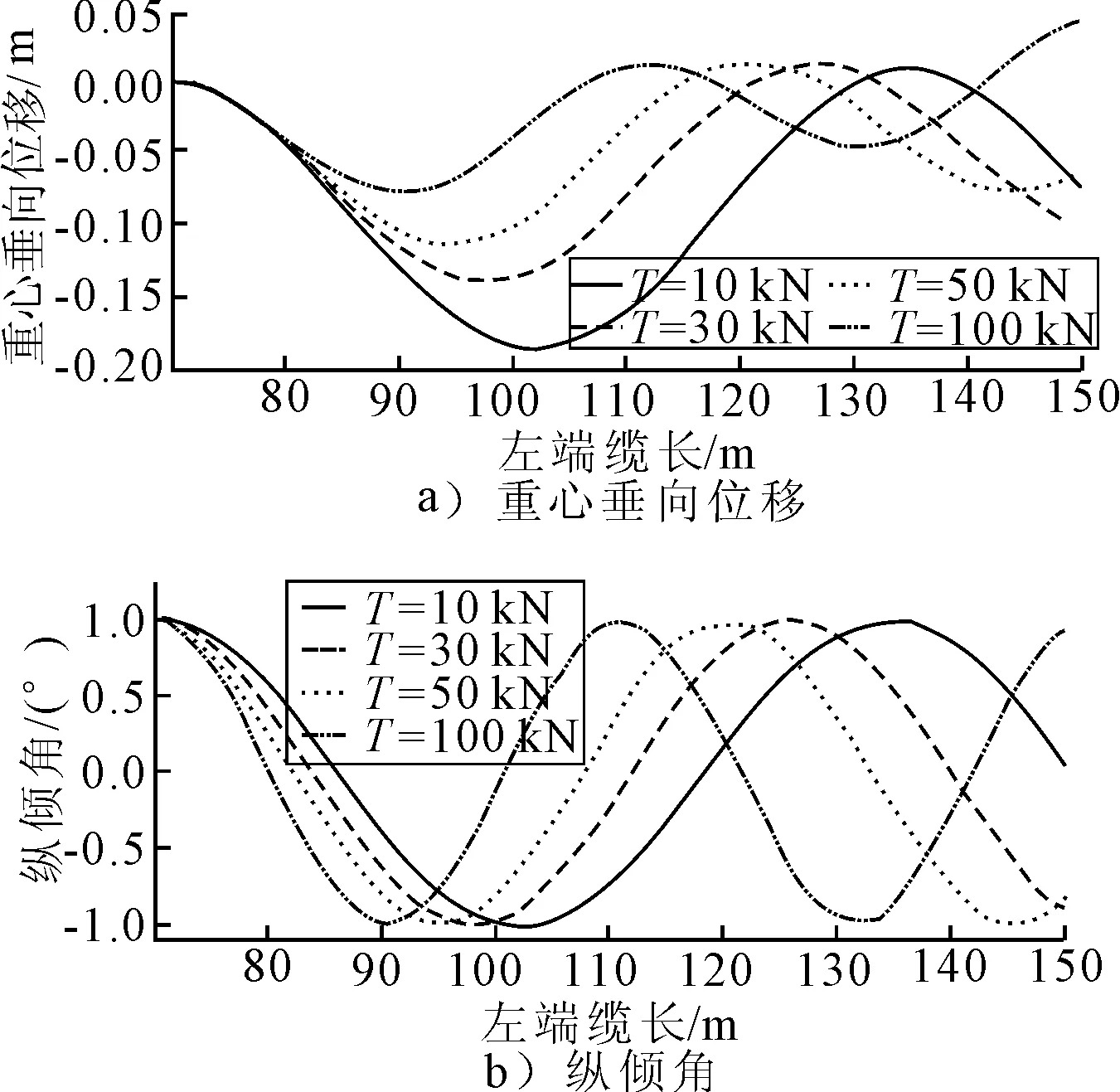
图7 初始纵倾角为1°时系统的运动响应

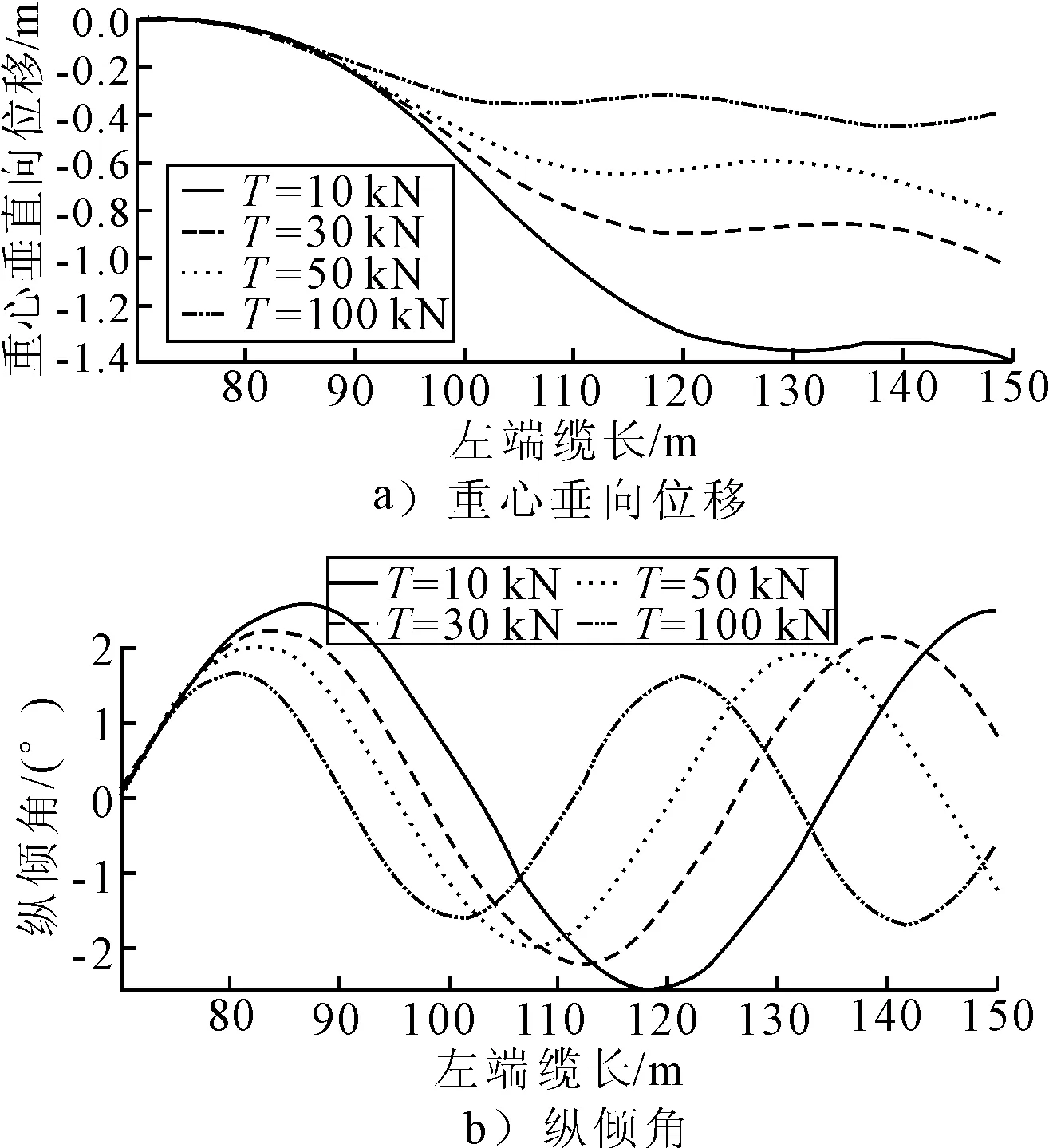
图8 初始纵摇角速度为1 (°)/s时系统的运动响应

当预紧力T=50 kN时，模型重心位移与纵倾角的最大超调量均较小，运动较为平缓。因此设定拖缆的预紧力为50 kN。运用同样的方法评估其它试验航速下的系统运动特性，确定合适的预紧力。文献[5]基于试验结果给出了不同航速下拖缆预紧力的建议值(见表1)，可看出，本文的计算结果与文献[5]给出的结果相比稍偏大，但趋势一致，认为本文的计算具有较高的可信度。

4 操舵工况下的系统运动响应分析

大尺度水下综合试验模型在进行试验研究时，有两种典型工况：①在整个匀速试验段舵保持某一舵角固定不变，在这种工况下激励力和激励力矩都是恒定值；②持续不断地进行正弦操舵，在这种工况下激励力和激励力矩都呈正弦变化。有必要对其运动特性进行计算校核，以保证模型运动稳定性与安全性。由于试验模型以4 m/s速度向前运动是主要试验工况，因此仍然以此工况为例计算试验模型的运动特性。

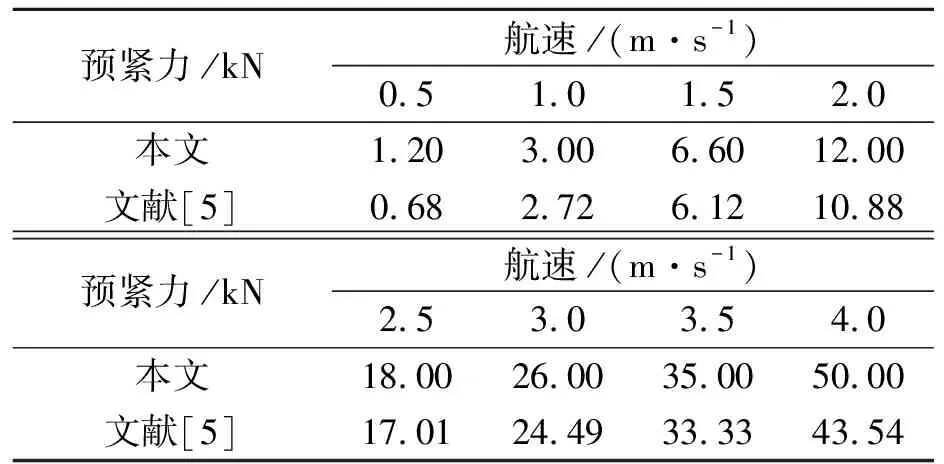
表1 不同航速下拖缆预紧力建议值对比

4.1 恒定舵角工况

试验模型艉升降舵舵面积A=2 m2，展弦比λ=2.08，翼剖面为NACA0018，求得舵角30°时激励力的最大值：F0=11.2 kN，M0=112 kN·m。计算不同大小的力和力矩作用下，系统的重心垂向位移和纵倾角响应，结果见图9。为保证试验模型试验过程中的运动稳定性和安全性，应限定该工况下舵角应不大于15°。

图9 恒力作用下的系统响应

4.2 正弦操舵工况

正弦操舵工况下操舵造成的激励力和激励力矩都是正弦形式的，若忽略相位影响，则还须确定激励频率与幅值。忽略频繁操舵时的记忆效应，简单计算激励幅值；由振动理论可知，当外激励的频率接近固有频率，系统发生共振，运动响应较剧烈，因此激励频率应落在系统的固有频率附近。

1) 激励力幅值。上节已算出舵角为30°时，舵的最大激励力和激励力矩分别为11.2 kN及112 kN·m，设定舵激励力在1～11.2 kN范围内变化，舵激励力矩在10～112 kN·m范围内变化。

2) 激励力频率。由图4可知，当拖缆预紧力为50 kN时，系统的垂荡固有频率在0.015 Hz附近变化，系统纵摇固有频率在在0.08 Hz附近变化。因此，可设定计算频率为0.01～0.30 Hz。

3) 计算结果与分析。分别计算操舵频率在垂荡固有频率附近和纵摇固有频率附近时的系统响应，因其计算结果数据较多，仅列出模型在整个运动过程中的最大重心位移和最大纵倾角响应，结果见图10。

由图10可见，当激励力的频率不断变化时，系统的最大重心垂向位移出现两个明显的峰值，分别对应于两个固有频率，对应于垂荡固有频率的峰值要明显大于对应于纵摇固有频率的峰值；而最大纵倾角响应只存在一个明显的峰值，对应于纵摇固有频率，这与文中得出的规律是相同的，即垂荡运动对纵摇运动产生的影响要小于纵摇运动对垂荡运动产生的影响。

图10 共振频率附近系统的响应

由振动的一般理论可知，当广义外激励力的频率在共振频率附近时，系统的响应将会非常大，运动有可能会振荡发散。但是在计算中，系统的响应不是十分大，究其原因是系统的共振固有频率非常小，亦即固有周期非常大，固有周期与试验模型向前运动的时间处于同一个量级，试验模型的运动过程只经历了不超过2个固有周期，系统的运动发散还未来得及充分形成，整个试验过程便已结束。如果减小模型的速度，亦即增大系统的运动时间，而保持其预紧力、激励力不变，则系统又可能发生运动发散。

用具体的算例说明这一问题。从图11可以看出，试验模型的前向运动速度若为0.4 m/s，系统的运行时间变为200 s，整个运动过程经历了约3个垂荡固有周期或10个纵摇固有周期，振荡已经充分发散。事实上，系统产生大重心垂向位移和大纵倾之后，文中所作出的相关近似已不成立，系统的非线性效应也会体现出来，实际的重心位移和纵倾角不会这么大。

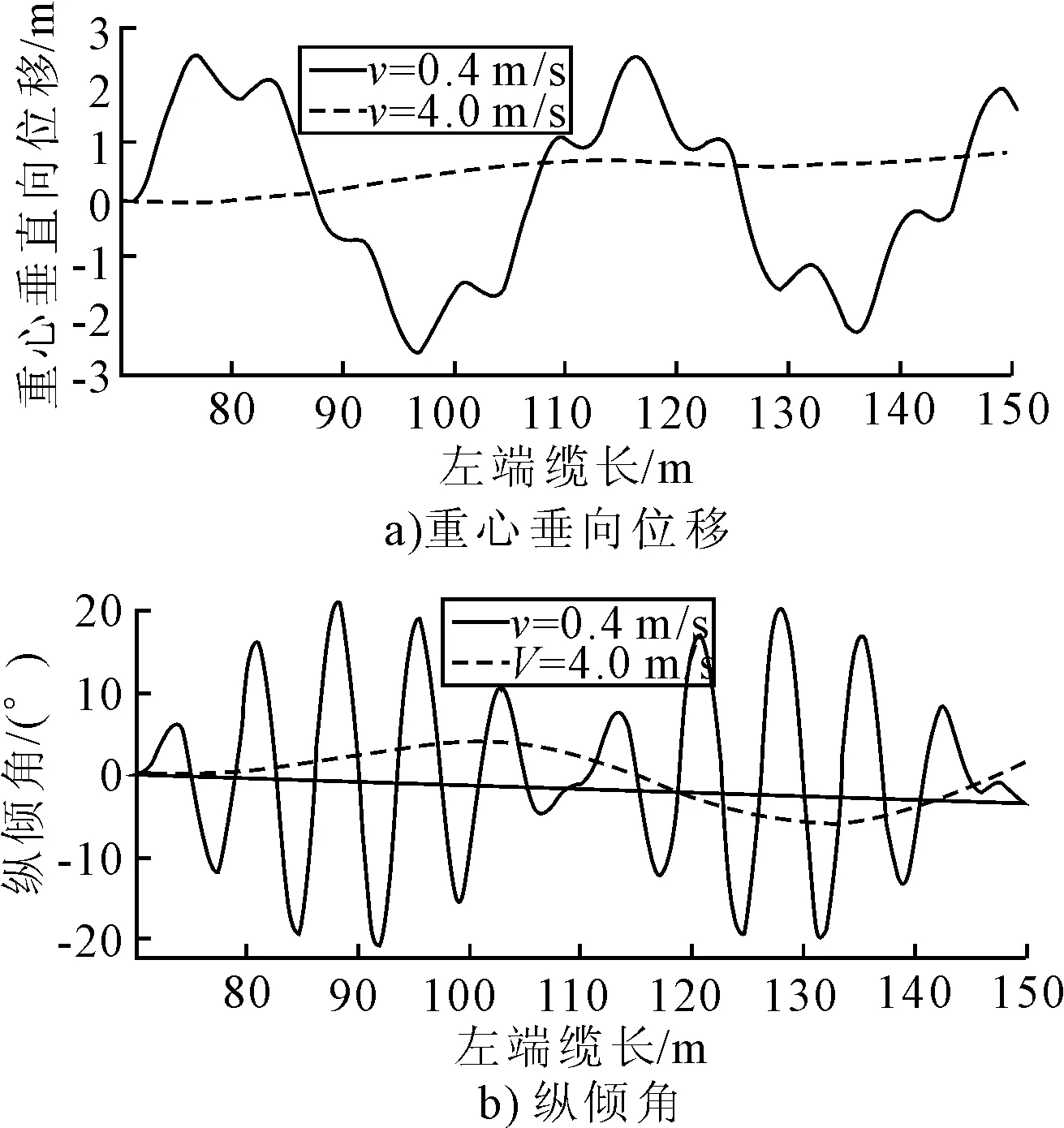
T0=50 kN；F0=11.2 kN；M0=112 kN·m；w=0.05 Hz

当试验模型以4 m/s的速度向前运动时，在激励力幅值不大于7 kN的条件下，模型的最大重心位移不大于1.3 m，最大纵倾角不大于6°，最大端部位移不大于1.7 m。正弦操舵工况与恒定舵角工况相比，最大舵角的限制可适当放宽。为保证试验模型的安全性，正弦操舵工况下最大舵角可适当放宽至约18°。

当试验模型以其它速度向前运动时，按表1的数值改变预紧力，可保证整个运动过程经历较少的固有周期数，使共振不会充分形成、发展。并且速度降低之后，舵激励力和激励力矩将会急剧减小，系统的响应不会很大，可以保证试验模型在不同试验航速下的运动稳定性与安全性。

5 结论

为保证试验模型试验过程中的运动稳定性和安全性，应设定恒舵角工况下舵角不宜超过15°，正弦操舵工况下舵角不宜超过18°。

[1] BYSTORM L.Simulation of submarine recovery procedures in case of flooding[C]∥ Warship 2002,International symposium on Naval submarines. London UK, 2002.

[2] 任 凯.破损舰艇拖航稳度分析[J].船舶，2007，18(2)：16-19.

[3] 郝英泽，胡 坤，刘百顺.潜艇水下破损定深操纵方法仿真研究[J].船海工程，2010，39(2)：111-113.

[4] 何春荣，赵桥生，马向能.潜艇大攻角操纵运动预报[J].船舶力学，2010，14(4)：340-346.

[5] 杨仁友.综合试验平台线型初步方案与缆绳载荷初步分析报告[R].无锡：中国船舶科学研究中心，2010.