水下近场爆炸作用下抗爆结构动响应特性研究

，，，

(1.哈尔滨工程大学 船舶工程学院，哈尔滨 150001;2.中国船舶及海洋工程设计研究院,上海 200011)

1 模型描述

1.1 抗爆结构模型描述

抗爆结构模型由两部分组成，上部为主体结构——钢结构，下部为抗冲结构——气囊。其中钢结构的长为2 m，宽为2 m，高为0.24 m；抗爆抗冲击结构的长为2 m，宽为2 m，高为0.08 m，其内部气体压力为0.3 MPa。炸药距气囊底部的距离为1，其结构示意及有限元模型见图1、2。

图1 抗爆结构示意(单位：m)

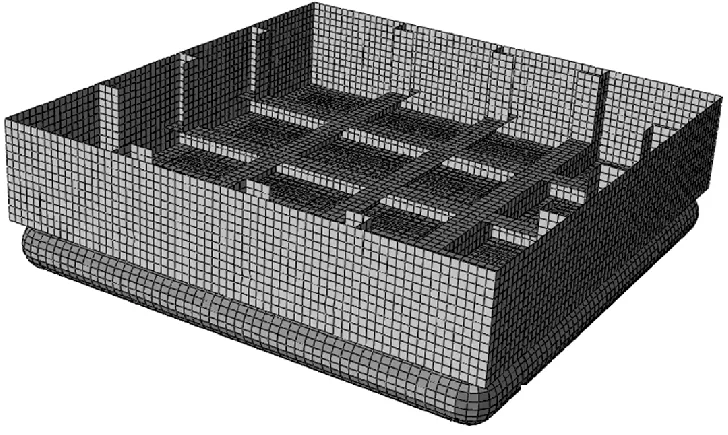
图2 抗爆结构有限元模型

1.2 材料参数

模型中钢结构采用普通Q235钢，基本参数为密度ρ=7 850 kg/m3，弹性模量E=210 GPa，泊松比υ=0.3，屈服应力σy=235 MPa。应变速率的影响采用

(1)

式中：σy——材料的静态屈服极限；

D、P——参数，依材料而定，本算例D=40，p=5[1]。

气囊中橡胶的密度ρ=1 150 kg/m3，其材料模型应用应变势能中的Mooney-Rivlin模型[2-3]，其应变能密度为

(2)

本算例中C10=17 600，C01=4 330。

水的状态方程采用多项式方程[4]。

1) 在压缩状态下的压力。

p=a1μ+a2μ2+a3μ3+(b0+b1μ+b1μ2)ρ0e0

(3)

2) 在膨胀状态下的压力。

p=a1μ+(b0+b1μ)ρ0e0

(4)

式中：ρ0——初始密度；

a1、a2、a3、b0、b1——系数，取

a1=2.19 GPa，a2=9.224 GPa，

a3=8.767 GPa，b0=0.493，

b1=1.393 7；

μ=η-1。

其中：η——扰动前后的密度比。

空气采用理想气体，用理想气体状态方程描述，而且满足γ定律状态方程，其中气体初始压力pA=3 MPa。

爆炸冲击波载荷的大小根据Geers-Hunter模型[5]进行计算，分别取药量为0.06、0.09、0.15、0.25、0.55 kg当量的TNT进行球形装药，位于气囊中心正下方的1 m处。

1.3 流固耦合效应

采用耦合欧拉/拉格朗日(coupled eulerian/lagrangian，CEL)法模拟流固耦合效应。

2 模型计算

抗爆结构在上述药量的水下爆炸作用下，橡胶气囊在冲击波作用下先发生破坏以致失效，当气囊失效后，水流和钢结构底部接触，经过气囊衰减后的冲击波压力直接作用在钢结构上，引起钢结构的响应。这一过程极其复杂，直接建模求解难以得到满意的结果。因此，对这一过程进行适当的简化以期得到较为准确的结果。以下以药量0.06 kg的工况为例阐述抗爆结构模型计算简化的过程。

由于气囊材料为橡胶，因此采用橡胶应变值大于1作为橡胶气囊破坏的判据。在此药量的爆炸冲击波载荷作用下，橡胶气囊底面先呈凹球状，随着冲击波的继续作用，底面中点先与气囊顶面接触，最后在t=0.16 ms时刻气囊的整个底面与顶面完全接触，此时其变形值已经接近0.08 m，等于橡胶气囊的高度，即橡胶气囊已经贴到了钢结构底部，橡胶气囊的应变值已达1.145，大于1，因此认为此时橡胶破坏，其橡胶气囊破坏时位移、应变云图及舯剖面的变形见图3～6。

图3 橡胶气囊位移云图

由图5、6可见，当橡胶气囊破坏时，水流已经和钢结构底部接触，但由于气囊中的空气和橡胶阻抗不同，冲击波在气囊中传播时已经100%衰减，因此水流在和钢结构底部接触之前钢结构的响应为0。此时，由于气囊已经破坏，对以后的计算没有影响，并且水流接触钢结构后冲击波的衰减规律遵循冲击波在自由场中的衰减规律，所以将橡胶气囊模型除去，并提取气囊破坏时接触钢结构的水中的冲击波压力作为钢结构的外载荷，直接加载到钢结构上，计算钢结构的响应。

图4 橡胶气囊应变云图

图5 橡胶气囊破坏时舯剖面的变形

图6 气囊破坏时的钢结构应力云图

3 计算结果分析

通过以上假设对模型计算进行简化得到了抗爆结构的结构响应，下面以药量为0.06 kg的工况下的钢结构底面中心点的计算结果为例进行对比分析，并给出所有工况下有气囊和无气囊时钢结构的响应峰值，以比较抗爆结构的抗爆效果。

3.1 应力响应

从图7可知，无气囊时钢结构应力值达到328 MPa，而有气囊时的应力值为307 MPa；而且从图8可以看出，同一位置处的任意时刻，有气囊钢结构比无气囊钢结构的Mises应力小，说明气囊的存在起到了衰减冲击波的作用，起到了一定抗爆效果。

所有工况下，有气囊和无气囊时钢结构应力峰值及衰减比见表1。从表1可知，橡胶气囊使钢结构的应力值有所降低。

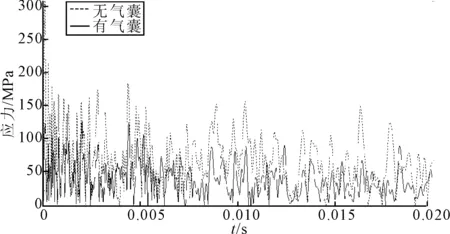
图7 中心点Mises应力

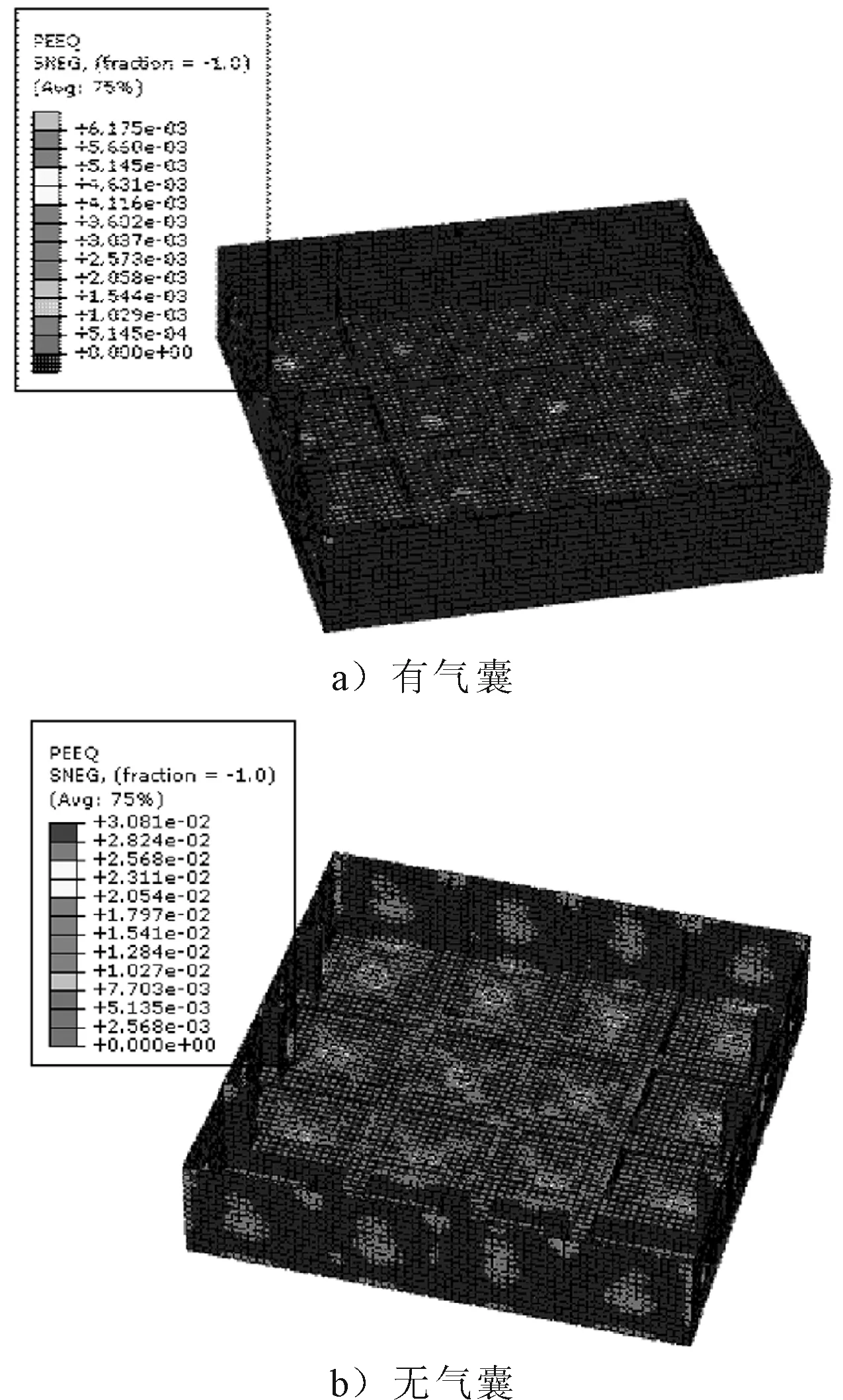
图8 钢结构应力云图

表1 钢结构应力峰值

3.2 等效塑性应变响应

从图9可知，无气囊时钢结构等效塑性应变值达到0.031，而有气囊时的等效塑性应变值为0.006, 且无气囊时产生塑性应变的区域远大于有气囊的结构，并且从图10可看出，在同一位置的任意时刻，有气囊钢结构比无气囊钢结构的等效塑性应变小很多，说明气囊的存在大大降低了钢结构的等效塑性应变值。

图9 中心点等效塑性应变值

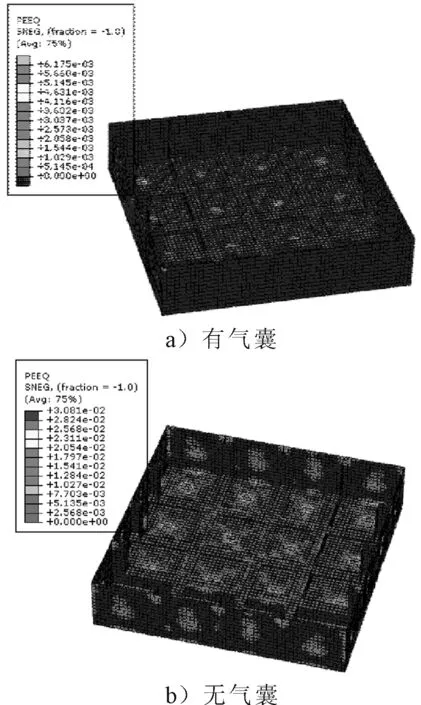
图10 钢结构等效塑性应变PEQ

所有工况下，有气囊和无气囊时钢结构等效塑性应变峰值及衰减比见表2。

表2 钢结构等效塑性应变峰值

从表2可知，在一定药量以下，随药量的增大其衰减比保持在0.3左右，并无较大变化，说明此药量内气囊对结构起到较好的抗爆效果，但超过此药量时，其衰减比αp随药量的增大而迅速增大，抗爆效果也随之下降。

3.3 加速度响应

从图11与图12可知，有气囊时结构的加速度值约为无气囊的0.5倍，说明气囊的存在能较好地改善结构的冲击环境。

图11 中心点加速度值

图12 钢结构加速度

所有工况下，有气囊和无气囊时钢结构加速度峰值及衰减比见表3。从表3可知，在药量低于0.15 kg时，气囊能较好地改善其结构的冲击环境，其衰减比αa达0.55左右，但随着药量的增大，其衰减比αa迅速增大，说明在一定药量范围内的近场爆炸中，气囊对结构的冲击环境的改善有良好效果，但药量增大时，改善效果明显下降。

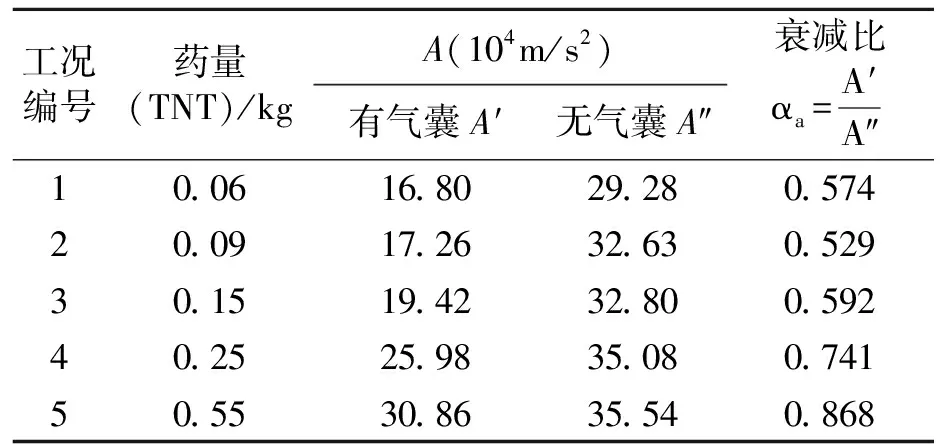
表3 钢结构加速度峰值

4 结束语

对于一定药量范围内的近场爆炸，抗爆结构中的橡胶气囊结构能有效地衰减冲击波的作用，对降低钢结构的应力峰值、等效塑性应变及加速度峰值有明显效果，能有效地改善结构的冲击环境，起到了良好的抗爆效果；但随药量的增大，其抗爆性能随之下降，对改善结构冲击环境的效果也随之降低。

[1] 王自力.船舶碰撞损伤机理与结构耐撞性研究[D].上海：上海交通大学,2000.

[2] 龚积球，龚震震，赵熙雍.橡胶件的工程设计及应用[M].上海：上海交通大学出版社，2003.

[3] 弗雷克利K,佩恩P K.橡胶在工程中应用的理论与实践[M].杜承泽,唐宝华,罗东山,等译.北京:化学工业出版社, 1985.

[4] LIU G R, LIU M B.光滑粒子流体动力学——一种无网格粒子法[M]. 韩 旭，杨 刚，强洪刚，等译.长沙：湖南大学出版社,2005.

[5] GEERS T L, HUNTER K S. An integrated wave-effects model for an underwater explosion bubble[J]. Journal of the Acoustical Society, 2002,111(4):1584-1601.