高速铁路桥墩墩顶横向水平位移控制值算法的研究

郭新伟

(铁道第三勘察设计院集团有限公司,天津 300142)

1 《高速铁路设计规范》对高速铁路桥墩墩顶横向水平位移限值的规定及相关思考

目前,世界上铁路发达国家规范对墩顶横向水平位移限值主要是通过相邻结构物水平折角的限值来表示[1]。我国把旅客列车运行速度达到200 km/h及以上的铁路统称为高速铁路[2]。到目前为止,我国发行的所有200 km/h及以上铁路规范,对墩顶横向水平位移引起的桥面处梁端水平折角限值均取1.0‰rad。梁端水平折角如图1所示。

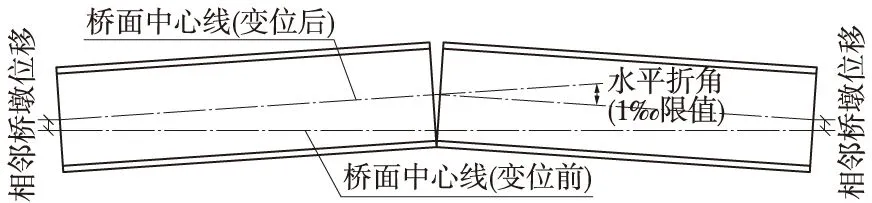
图1 梁端水平折角示意

由于《高速铁路设计规范》(TB10621—2009)没有直接给出高速铁路桥墩墩顶的横向水平位移限值,铁路设计者在实际工作中,需要根据规范对梁端水平折角的限值来反算桥墩墩顶的横向水平位移控制值,以指导桥墩和基础的设计。根据规范及其条文解释：梁端水平折角的产生是由于梁端处桥墩墩顶横向水平位移有差别而引起的,根据三角关系,梁端水平折角与相邻两孔(联)梁(对于简支梁为一孔梁,对于连续梁为一联梁)的交点距、相邻两孔(联)梁梁端处桥墩墩顶横向水平位移差值有关。

每孔(联)梁的交点距都是精确已知的,而相邻两孔(联)梁梁端处桥墩墩顶横向水平位移的差值确是随机变化的。因此,在桥墩或基础的施工图设计阶段,根据梁端水平折角限值来反算墩顶横向水平位移限值是无法实现的。若想获得近似的墩顶横向位移限值以指导设计,必须对相邻两孔(联)梁梁端处桥墩墩顶横向水平位移的差值作出某种合理假设。

2 对实际反算算法的调查研究

在桥墩和基础的设计中,必须通过某种反算算法以获取近似的墩顶横向位移限值来指导设计。本文对墩顶横向水平位移限值的反算算法进行了长期调查研究,其中“通桥(2009)4201”、“通桥(2009)4301” 通用图提出的反算算法最具代表性。

2.1 部颁通用图反算算法

部颁通用图通过以下方法来反算目标桥墩的墩顶横向水平位移限值：目标桥墩墩顶的梁端水平折角达到1‰rad的限值时,假设目标桥墩相邻一孔(联)梁的另一侧梁端处的桥墩墩顶横向水平位移为零,然后根据目标桥墩相邻两孔(联)梁的交点距L与目标桥墩处梁端水平折角α0的关系,推算目标桥墩的墩顶横向水平位移Δ,推算结果即为目标桥墩的墩顶横向水平位移限值。计算图示如图2所示。

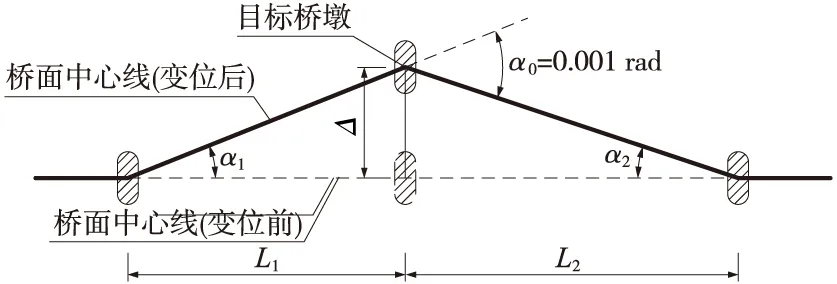
图2 墩顶横向水平位移限值计算示意

由三角关系可得

α1+α2=α0=0.001 rad

(1)

由于0.001 rad比较微小,由弧度关系可得

Δ≈α1L1=α2L2,即：α1=Δ/L1、α2=Δ/L2

(2)

将公式(2)代入公式(1),即可得桥墩墩顶横向水平位移限值Δ

(3)

式中α0——梁端水平折角限值，rad；

α1、α2——变位前、后桥面中心线夹角,rad；

L1、L2——目标桥墩相邻两孔(联)梁的交点距,m。

Δ——桥墩墩顶横向水平位移限值,mm。

实际上,以上反算算法是基于“单墩位移”模式提出的,由于作出了“目标桥墩相邻一孔(联)梁的另一侧梁端处的桥墩墩顶横向水平位移为零”的假设,墩顶横向位移限值仅与“目标桥墩相邻两孔(联)梁的交点距L”有关。显然,这种假设对于反算横向位移限值是最方便、最直接的,因而应该是合理的假设。需要说明的是,部颁通用图提出的墩顶横向位移限值仅适用于常用跨度简支梁组合。

2.2 目前在建高速铁路项目采用的反算算法

对目前在建或待建的多条高速铁路(或客运专线)进行了调查,设计者在反算墩顶横向位移限值时均无一例外地采用了部颁通用图的算法,直接套用公式(3)。这显然是部颁通用图的示范效应带来的结果。

随着桥梁技术发展的日新月异,不同跨度的桥梁不断涌现。高速铁路上除了常用的20 m、24 m、32 m简支梁以外,(32+48+32)m、(40+64+40)m、(48+80+48)m、(60+100+60)m、(80+128+80)m等连续梁也是普遍存在的。基于“单墩位移”模式提出的公式(3)是否对已出现的所有桥梁形式都适用,需要做进一步的研究。

3 对目前反算公式适用性的研究

按照一般理解,只要每个桥墩的墩顶横向水平位移不超过反算所得的位移限值,即可认为全桥的梁端水平折角不超限。正常情况下,运营中的铁路出现单独一个桥墩发生墩顶横向位移情况的概率很小,一般是局部范围内的一群桥墩同时发生墩顶位移,每个桥墩的墩顶位移有大有小。当一群桥墩同时发生墩顶横向位移,且横向位移均不超过按公式(3)反算所得的位移限值时,桥墩处的梁端水平折角是否全部满足规范要求是本文研究的内容。

3.1 研究方法

考虑3个桥墩同时发生墩顶横向位移的情况。计算图示如图3所示。

图3 3个桥墩同时发生墩顶横向位移示意

为了模拟孔跨的变化、墩群的墩顶横向位移差,同时为了简化计算,做以下假设。

(1)前3孔梁均为常用跨度梁(即Lc=20.7、24.7、32.7 m)且按等跨布置,第4孔(联)梁为任意跨度梁。

(2)首、尾墩的墩顶横向位移(即Δc、Δb)均达到了按公式(3)反算所得的位移限值。显然,此时首、尾墩处的梁端水平折角αc、αb均不超1.0‰的限值。

(3)中间墩的墩顶横向位移在0～Δc随机变化(即变化系数K=0～1)。

首先,由假设(2)可知

(4)

(5)

然后,根据弧度关系可得

(6)

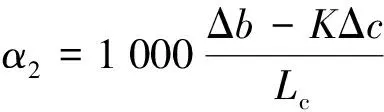
(7)

根据对角相等关系,可得中间墩处的梁端水平折角αx

αx=α1+α2

(8)

将公式(4)～(7)代入公式(8)可得

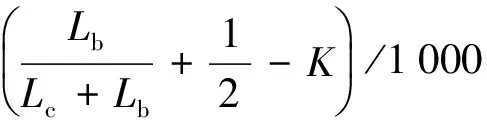
(9)

式中Lc——常用跨度简支梁的交点距，20.7、24.7、32.7,m；

Lb——任意跨度梁一孔(联)梁的交点距,m；

K——位移变化系数，取0～1。

根据公式(9),可以研究在孔跨组合随机变化、墩顶横向位移差随机变化的情况下,中间墩处的梁端水平折角的变化。

3.2 研究结果

(1)常用跨度简支梁组合的情况

Lb按常用跨度简支梁取值,即Lb=20.7、24.7、32.7 m时,计算结果如图4～图6所示。

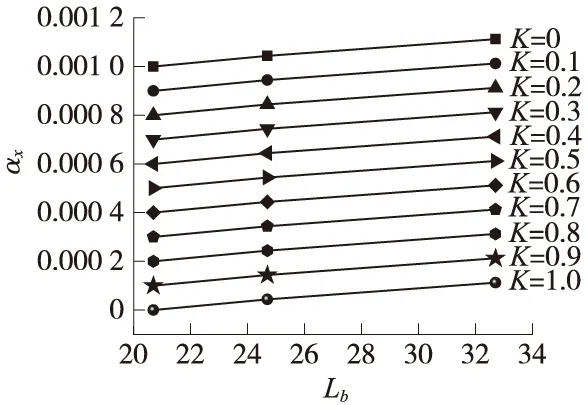
图4 Lc=20.7 m时αx变化曲线

图5 Lc=24.7 m时αx变化曲线

图6 Lc=32.7 m时αx变化曲线

K值反映了1孔简支梁两端桥墩的墩顶横向刚度比,合理情况下,该刚度比值在1～5,即K>0.2。由图4～图6可以看出,当K≥0.1时,均有αx≤1.0‰rad。因此,可以认为利用公式(3)反算所得的墩顶横向位移限值对于常用跨度简支梁(即20、24、32 m简支梁)是完全适用的,部颁通用图给出的桥墩墩顶横向水平位移限值是正确的。

(2)常用跨度简支梁与连续梁组合的情况

Lb按常用跨度连续梁：(32+48+32)m、(40+64+40)m、(48+80+48)m、(60+100+60)m、(80+128+80)m取值,即Lb=113.6、145.7、177.7、221.7、290.0 m时,计算结果如图7～图9所示。由图7～图9可以看出,当K>0.4时,才有αx≤1.0‰rad,即公式(3)不能保证正常情况下(K>0.2)所有桥墩处的梁端水平折角均满足规范。因此,对于常用跨度简支梁与连续梁组合的情况,利用公式(3)反算连续梁边墩的墩顶水平位移限值是有局限性的。显然,对于梁长与常用跨度连续梁相近的所有桥式结构,公式(3)都是有局限性的。

图7 Lc=20.7 m时αx变化曲线

图8 Lc=24.7 m时αx变化曲线

图9 Lc=32.7 m时αx变化曲线

4 对常用跨度简支梁与连续梁组合情况下反算算法的探讨

为获得合理的墩顶位移限值,以指导连续梁桥下部结构的设计,本文对公式(3)修正如下

(10)

式中Lc——与连续梁相接的简支梁的交点距：20.7、24.7、32.7 m;

Δb——连续梁边墩墩顶横向水平位移限值,mm。

将公式(10)代替公式(5)代入公式(8),可得

0～1.0‰

可见,利用公式(10)反算连续梁边墩的墩顶横向水平位移限值,可保证正常情况下所有桥墩处的梁端水平折角均满足规范,公式(10)是正确、合理的。

目前高速铁路连续梁均采用箱梁,纵、横向刚度很大,可视为刚体。因此,对于常用的3跨连续梁,根据跨度比例关系可得连续梁中墩的墩顶横向水平位移限值

(11)

式中p1——连续梁中跨跨度,m；

p2——连续梁边跨跨度,m；

Δz——连续梁中墩墩顶横向水平位移限值,mm。

多项设计实践表明,本文针对常用跨度连续梁提出的修正算法对于大跨度简支钢桁梁、大跨度简支系杆拱以及长联的多跨连续梁等也是完全适用的。

5 结论与建议

(1)由于规范没有直接给出高速铁路桥墩墩顶的横向水平位移限值,因此需要根据规范对梁端水平折角的限值来反算桥墩墩顶的横向水平位移控制值,以指导下部结构的设计。

(2)目前常用的反算算法对于常用跨度简支梁(即20、24、32 m)是完全适用的,而对于常用跨度连续梁以及梁长与之相近的桥式结构都是有局限性的。

(3)针对高速铁路常用跨度连续梁提出了修正反算算法,结果表明修正算法是正确、合理的。修正算法可推广使用到大跨度简支钢桁梁、大跨度简支系杆拱以及长联的多跨连续梁等桥式结构。

(4)对于高速铁路中出现的特殊、大跨、长联桥梁,建议进行梁端水平折角的测试研究,以确保高速铁路的安全性、舒适性。

[1] 孙树礼，周四思，杜宝军，等.桥墩墩顶横向水平位移限值的研究[J].铁道标准设计,2005(6).

[2] 孙树礼.高速铁路桥梁设计与实践[M].北京：中国铁道出版社,2011.

[3] 中华人民共和国铁道部.TB 10621—2009 高速铁路设计规范(试行)[S].北京：中国铁道出版社，2009.

[4] 甄津津.客运专线铁路常用跨度桥梁桥墩设计[J].铁道标准设计,2007(2).

[5] 许三平.京沪高速铁路徐沪段桥梁设计[J].铁道标准设计,2010(7).

[6] 王庭正.中德两国高速铁路桥涵设计的差异分析[J].铁道工程学报,2009(6).

[7] 杨继光.桥梁位移病害整治与思考[J].铁道标准设计,2004(5).

[8] 王淑敏.客运专线(48+3×80+48) m刚构-连续组合梁桥刚构桥墩设计研究[J]. 铁道标准设计,2007(2).

[9] 李运生,阎贵平,钟铁毅.影响铁路桥梁行车安全的因素—桥墩横向刚度问题的研究[J].中国安全科学学报,2004(2).

[10] 许建平.既有铁路桥墩横向刚度加固方案试验研究[J].铁道标准设计,2010(11).