城市连续梁桥双柱墩E2地震作用墩顶容许位移计算

杨一维， 郑凯锋， 张 锐

(西南交通大学， 四川成都 610031)

震害调查显示，在强烈地震动作用下，按规范设计的某些桥梁并不具备抵抗强震的足够强度，但是却仍没有倒塌或者发生严重破坏，是因为结构的初始强度并没有因为非弹性变形的加剧而过度下降，也即具有较好的延性。延性抗震理论不同于强度理论，它是通过特定部位的塑形变形，形成塑性铰，从而消耗地震能量，减小地震反应。对于双柱墩，墩顶仅受纵向荷载，产生纵向位移时，桥墩最大弯矩出现在墩底位置；当墩顶仅受横向荷载，产生横向位移时，桥墩最大弯矩出现在墩底和墩顶。当地震作用时，纵向变形时在墩底产生塑性铰，横向变形时墩顶和墩底均产生塑性铰，由此可见，采用统一的计算方法无法正确反映桥墩纵横向各自不同的力学特征，所以要分开考虑，分不同的计算方法计算两个方向的墩顶位移。目前的抗震设计规范[1]已采纳了延性抗震理论，规定E2地震作用下，墩顶纵向容许位移直接按照给定公式计算，但目前尚无公式可直接计算出墩顶横向容许位移，横向变形时，双柱墩由于框架效应在墩顶和墩底均产生塑性铰，无法直接推导出墩顶横向位移计算公式，所以需利用有限元软件对双柱墩进行非线性静力分析从而得到墩顶横向容许位移。因此，本文以某实际工程案例为背景，从力学原理出发，推导并验证了双柱墩墩顶纵向容许位移计算公式；采用Midas/Civil有限元数值模拟的方法，对双柱墩进行非线性静力分析(pushover)求得墩顶横向容许位移，并且阐述了计算方法和流程，为双柱墩墩顶容许位移计算分析提供参考。

1 工程概况

某城市预应力混凝土连续箱梁，两联6跨，主跨(3×32 m+3×32 m)，上部结构单箱三室箱梁，梁高1.6 m，顶板宽17.1 m，底板宽12.92 m，顶板厚250 mm，底板厚220 mm，腹板厚500 mm。主梁采用C50混凝土。上部结构构造见图1。

图1 上部结构构造(单位：mm)

下部结构采用双柱墩。交接墩采用双柱墩接盖梁形式，墩身高7.5 m，为1.6 m×1.3 m矩形截面。盖梁跨中高1.9 m，悬臂端部高0.9 m。承台高2.5 m。基础采用钻孔灌注桩基础，单个承台设置4根桩，桩径1 500 mm，桩长50 m。桥梁按7度设防，场地类型为Ⅰ类，分区特征周期Tg=0.35s。桥墩和盖梁采用C50混凝土，承台和基础采用C25混凝土。桥墩截面采用50根直径26 mm的HRB335级钢筋。下部结构构造见图2和图3，桥墩截面布筋见图4。

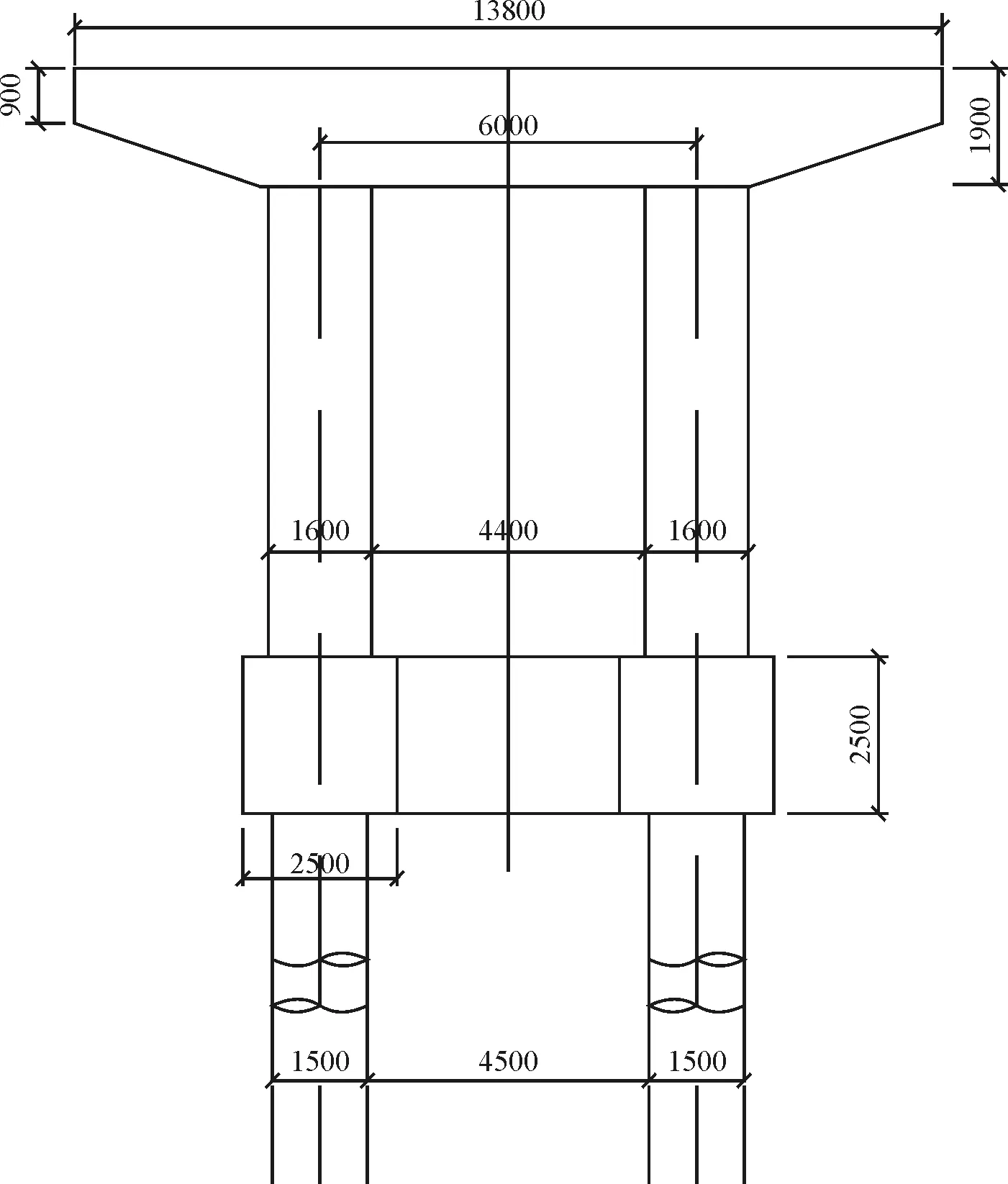
图2 下部结构构造(单位：mm)

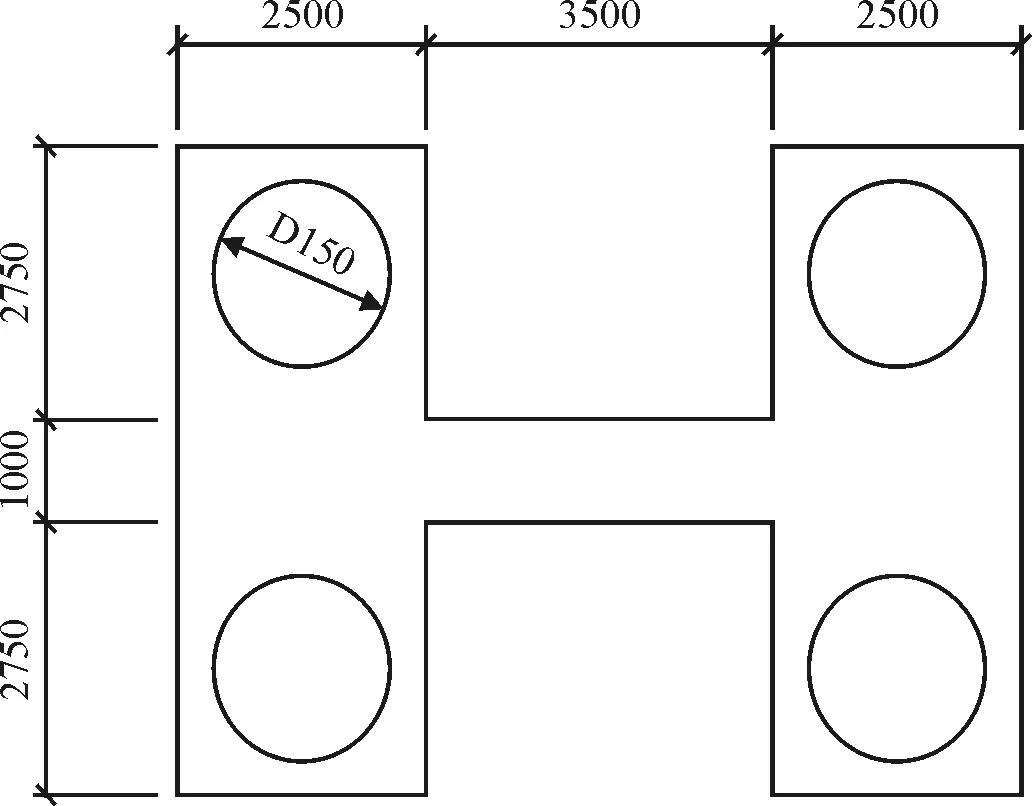
图3 承台横断面(单位:mm)

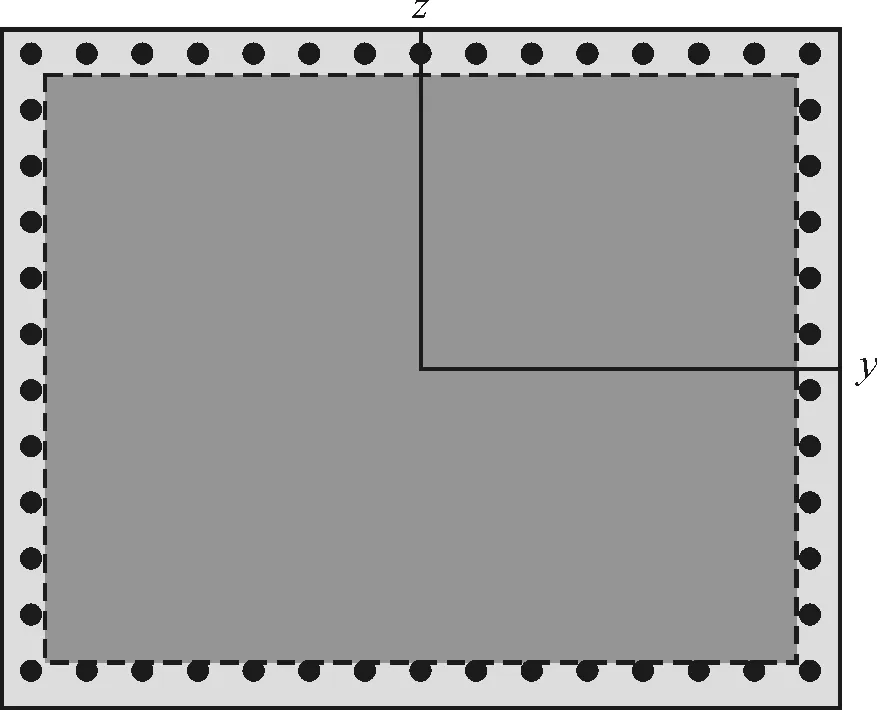
图4 桥墩截面布筋

2 有限元模型建立

利用Midas/Civil有限元分析软件分别建立整体空间模型和交接墩空间模型。利用整体模型计算得出上部恒载作用下支座的反力，将其以恒载工况下集中力的形式施加到交接墩空间模型的相同支座位置处。整体空间模型和交接墩空间模型见图5和图6。

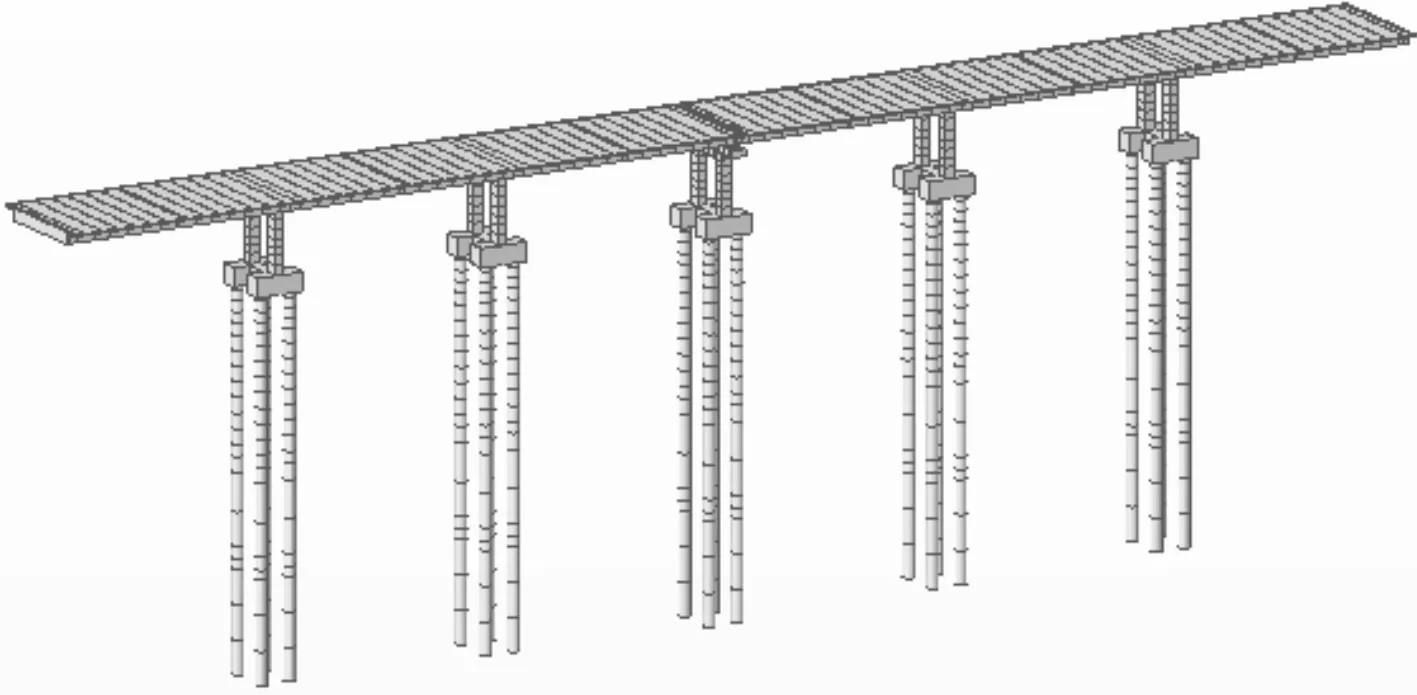
图5 整体空间模型

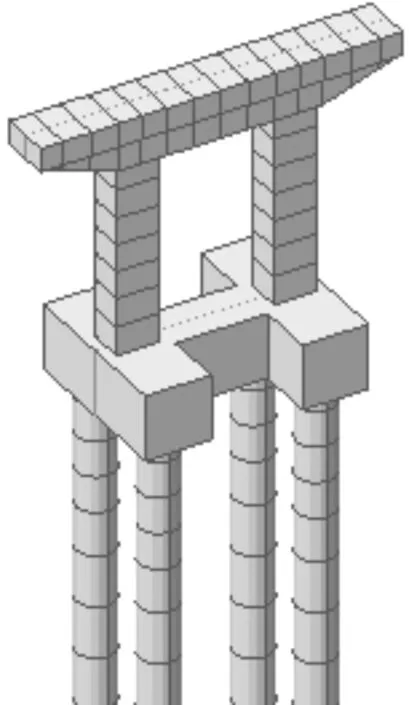
图6 交接墩空间模型

3 双柱墩墩顶纵向容许位移

3.1 理论推导

双柱墩纵向产生位移时，仅在墩底产生塑性铰，力学特征与单柱墩相同，采用与单柱墩相同的分析方法。

对于单柱式悬臂桥墩，其墩顶位移和桥墩的曲率分布存在如下关系：

Δ=∬φ(x)dxdx

式中：Δ为墩顶位移；φ(x)为曲率。

当变形未达屈服位移时，曲率沿墩高呈线性变化，变形超过屈服位移以后，形成塑性铰，依靠塑性铰的转动使得变形继续发展，此时曲率变化主要集中在塑性铰区域，塑性铰区域外基本不变化。

3.1.1 墩顶屈服位移

在墩底截面刚刚屈服时，可认为曲率沿墩高成线性分布：

式中：x为计算截面与墩顶之距；H为墩高；φy为屈服曲率。

代入Δ=∬φ(x)dxdx，可得墩顶的屈服位移Δy为：

Δy为墩顶屈服位移。

3.1.2 墩顶塑性位移

延性构件主要通过在特定位置形成塑性铰来提供延性，单柱墩潜在塑性铰区一般在墩底，所以在墩底截面达到极限状态时，引入“等效塑性铰长度”Lp的概念，即假设在墩底附近存在一个长度为Lp的等塑性曲率段，在该段长度内，截面的塑性曲率等于墩底截面的最大塑性曲率φp。由等效塑性铰长度Lp计算墩顶塑性位移Δp。

墩底截面达到极限状态时，桥墩的塑性转角可表示为：

θp=Lp(φu-φy)

Lp为等效塑性铰长度。同塑性变形的发展和极限压应变有关，一般采用经验公式，等效塑性铰长度经验公式见表1。

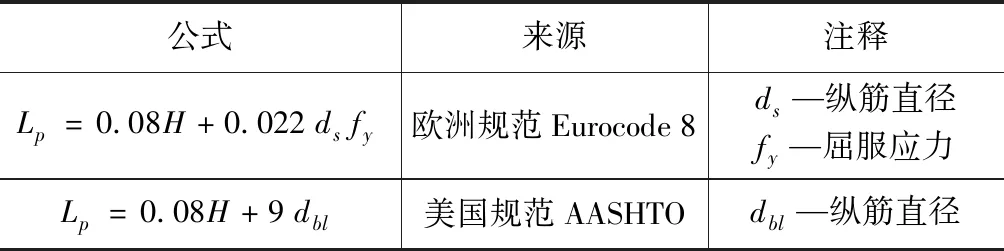
表1 等效塑性铰长度经验公式

φu为极限曲率。

假设在达到极限状态时，桥墩绕等效塑性铰区的中心点转动，则墩顶的塑性位移为：

Δp=θp(H-0.5Lp)

=(φu-φy)Lp(H-0.5Lp)

考虑延性安全系数K，塑性铰区域的最大容许转角可表示为:

K为延性安全系数，取2.0。

所以，墩顶塑性位移为：

Δp=θu(H-0.5Lp)

3.1.3 墩顶纵向容许位移

E2地震作用下，单柱墩墩顶容许位移Δu为墩顶屈服位移Δy与墩顶塑性位移Δp之和：

上式与规范[1]7.3.5条验证符合，双柱墩墩顶纵向容许位移可按上式计算。

3.2 墩顶纵向容许位移计算

由Midas/Civil有限元软件计算得出墩底等效屈服位移、极限曲率分别为：

φy=2.6×10-5cm-1

φu=4.1×10-5cm-1

等效塑性铰长度：

Lp=0.08H+0.022dsfy

=0.08×750+0.022×2.6×335

=79.2cm

取安全系数K=2，则塑性铰区域最大容许转角为：

墩顶纵向容许位移：

4 双柱墩墩顶横向容许位移

4.1 理论依据

E2地震作用下，双柱墩横向变形时，由于框架效应在墩顶和墩底均产生塑性铰，桥墩墩顶横向容许位移难以想独柱墩一样能推导出公式，所以规范[1]7.3.7条规定需对双柱墩盖梁处施加水平力，进行非线性静力分析，当墩柱的任一塑性铰达到其最大容许转角或塑性铰区控制截面达到最大容许曲率时，盖梁处的横向水平位移即为墩顶横向容许位移。

桥梁抗震分析主要有静力法、反应谱、时程分析法三种，双柱墩横向容许位移分析采用的是静力弹塑性分析(pushover)，属于非线性静力分析方法。该方法预先假定一种分布侧向力作用在结构上，考虑结构中的各种非线性因素，按设定步长逐步增加结构的侧向力或侧向位移，直到结构模型控制点达到目标位移或结构倾覆为止，由于考虑了塑性铰的设置，可以得到分别每步骤加载下结构进入塑性后的内力和位移状态。

4.2 计算流程

用非线性静力分析法计算横向容许位移时，由于需要进行迭代，采用单独的墩柱模型比整体模型更精确。具体计算步骤如下：

(1) 利用有限元分析软件计算出恒载作用下桥墩的最大轴力，结果见图7。

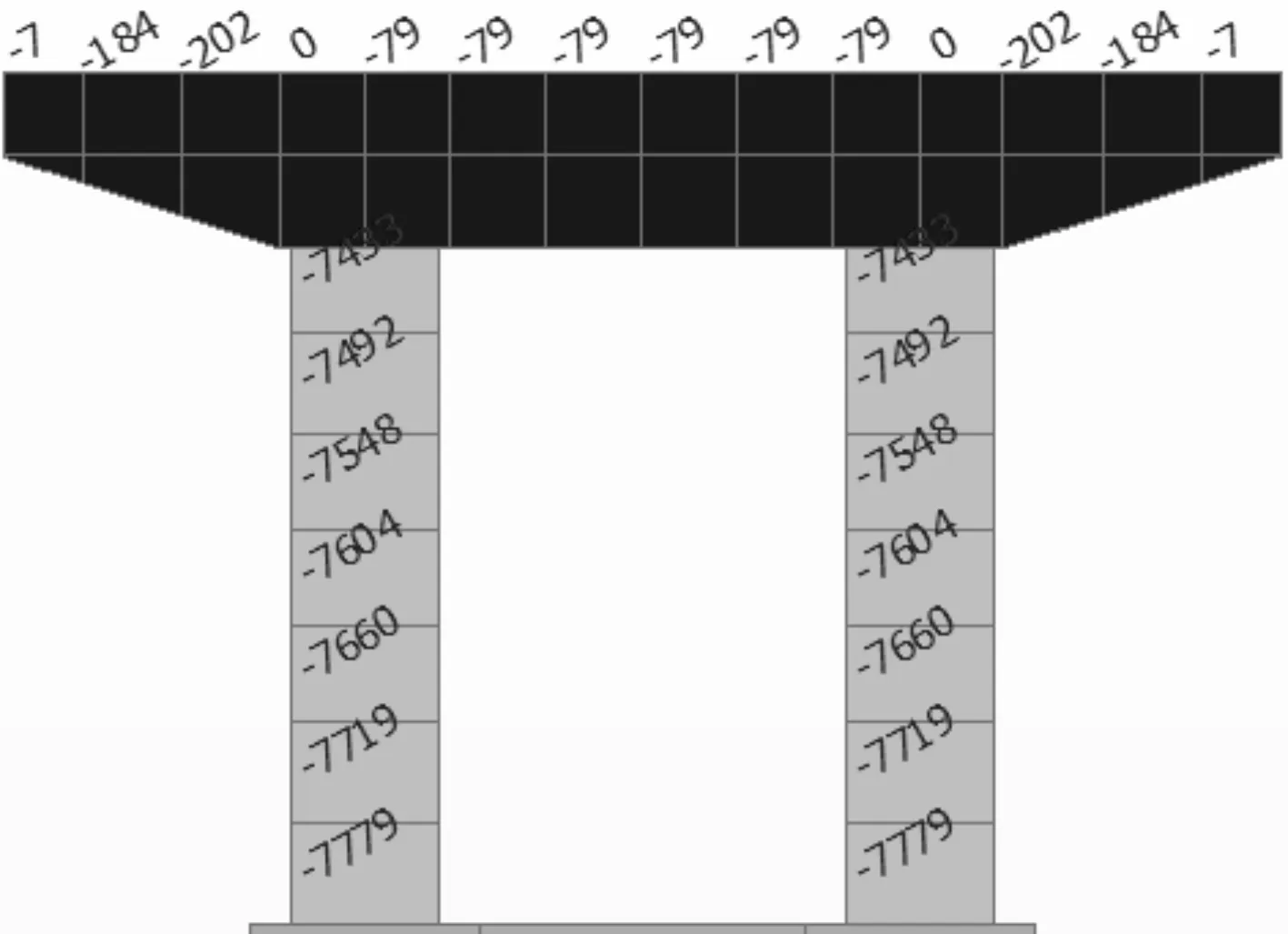
图7 恒载作用下桥墩轴力

由图7可知，桥墩在恒载作用下最大轴力发生在墩底，左墩和右墩均为-7 779 kN。

(2) 根据预先确定的混凝土及钢材的非线性本构关系计算桥墩截面的弯矩-曲率曲线(M-Φ曲线)，通过M-Φ曲线由桥墩最大轴力计算出各墩柱塑性铰区域截面的等效弯矩。

(3) 根据塑性铰区域等效弯矩计算出各单墩等效剪力，按V=∑Vi计算各单墩剪力值之和。

(4) 将水平合剪力V施加于盖梁质心处，计算合剪力和恒载组合作用下各桥墩的最大轴力，重复步骤2～步骤4进行迭代计算，直到相邻两次计算各墩柱剪力之和相差在10 %以内。轴力计算模式见图8， 迭代结果见表2。

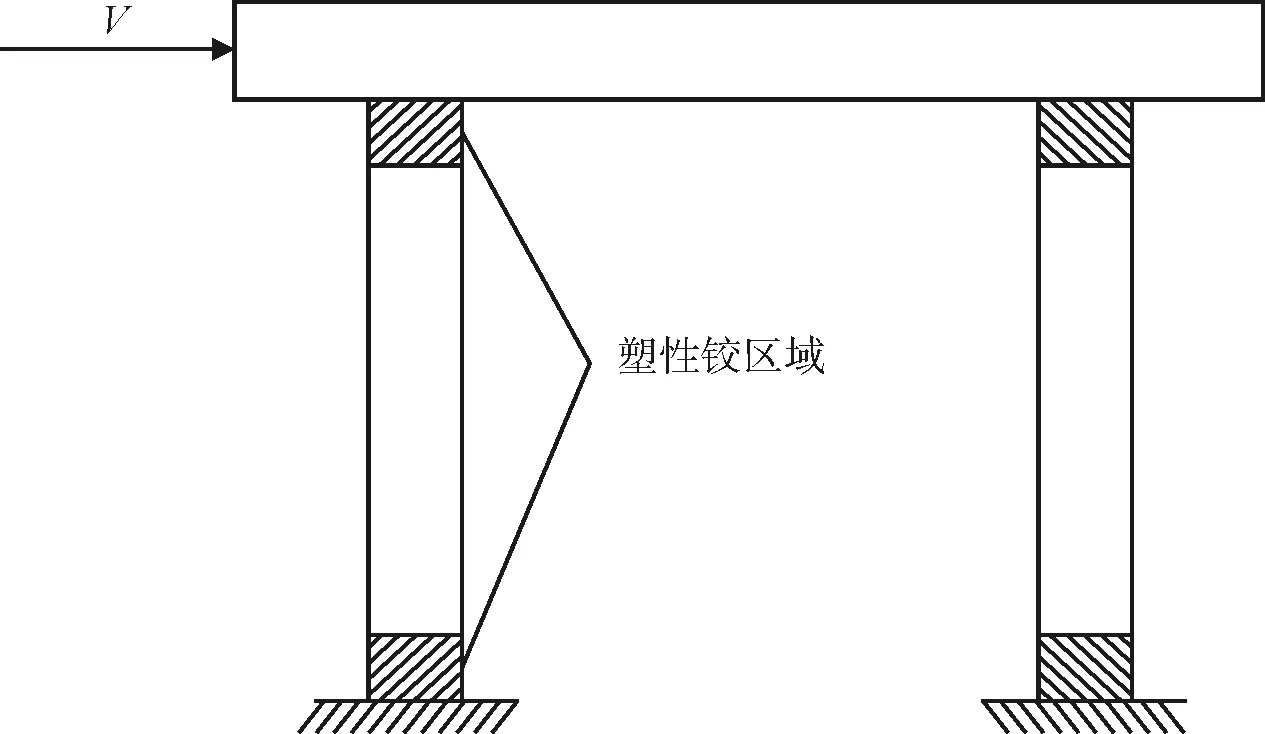
图8 轴力计算模式

由表2可知，迭代精度在第一次迭代时已满足，为使计算结果更精确，取第二次迭代结果，左墩墩底轴压力取14 094 kN，右墩墩底轴压力取1 464 kN。

(5) 通过M-Φ曲线由最终迭代得到的各单墩最大轴压力计算出各单墩极限破坏状态的曲率，最大容许曲率考虑为极限曲率除以安全系数，安全系数取2。单墩最大容许曲率见表3。

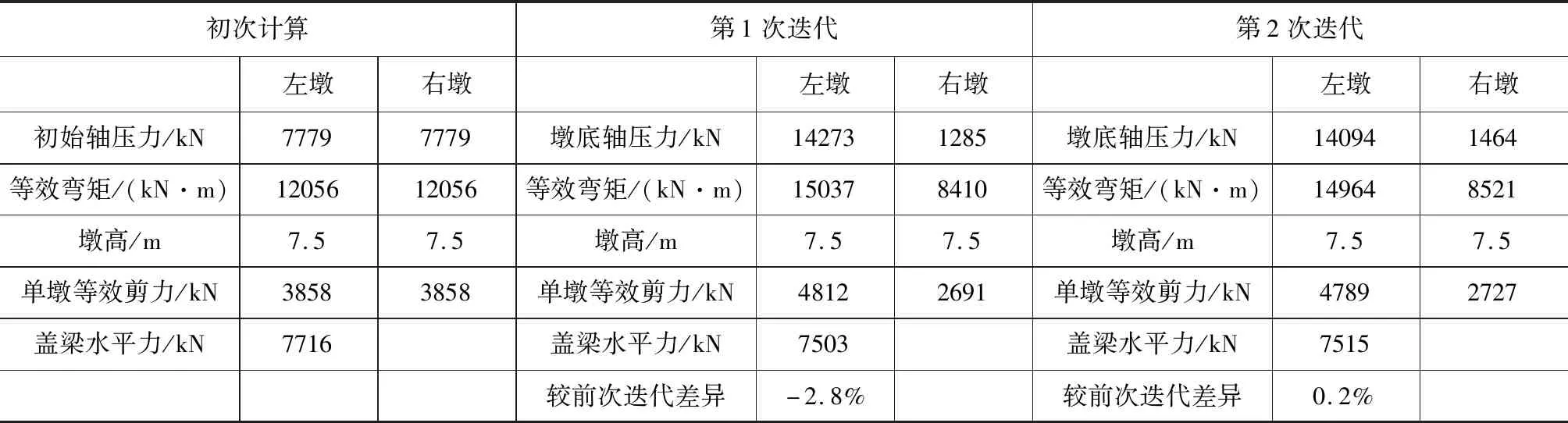
表2 迭代结果

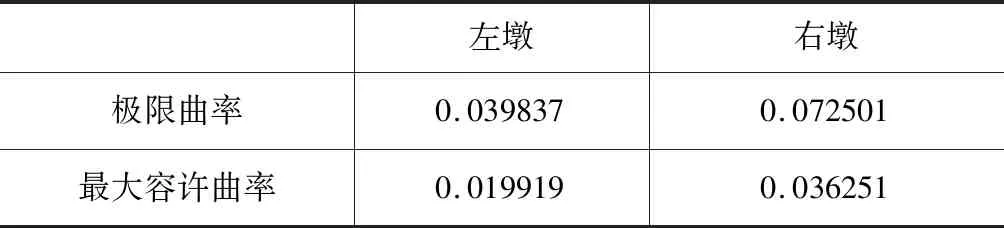
表3 单墩最大容许曲率

(6) 进行非线性静力分析，以桥墩盖梁中心的横桥向位移40 cm作为目标位移，盖梁上水平荷载分300步加载。当墩柱的任一塑性铰区控制截面达到其最大容许曲率时，盖梁处的横向水平位移即为墩顶横向容许位移。双柱墩横向容许位移计算模式见图9。

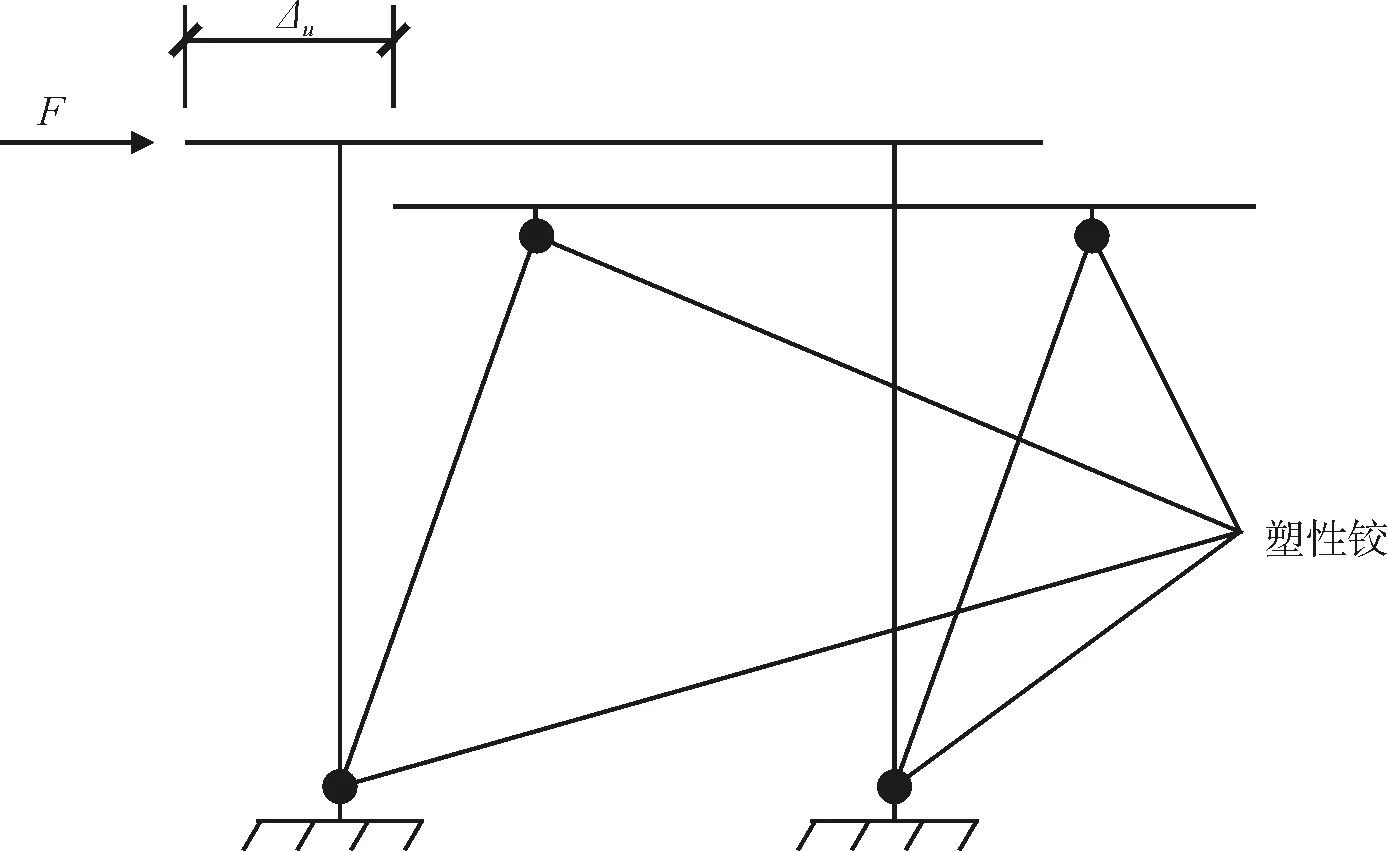
图9 双柱墩横向容许位移计算模式

查看pushover结果，左墩在第65步达到最大容许曲率0.019 919，右墩在第230步达到最大容许曲率0.036 251。所以取第65步的盖梁中心横向位移8.67 cm为双柱墩横向容许位移。

E2地震作用下，双柱墩左墩墩顶横向位移为6.72 cm，右墩墩顶横向位移为6.71 cm，均满足横向实际位移小于横向容许位移的要求。

5 墩顶位移验算

E2地震作用下，利用Midas/Civil有限元软件，对双柱墩墩顶位移进行验算，验算结果见表4。

由表4可知，E2地震作用下，双柱墩墩顶纵桥向和横桥向位移均小于分别的容许位移。

表4 墩顶位移验算

6 结论

(1) 结合某工程实例，从桥梁延性抗震理论出发，推导并验证了双柱式桥墩墩顶纵向容许位移的计算公式。墩顶纵向容许位移计算结果为5.3 cm。

(2) 对双柱式桥墩进行非线性静力分析，得到E2地震作用下双柱式桥墩墩顶横向容许位移，为实际工程设计提供参考。墩顶横向容许位移计算结果为8.67 cm。

(3) E2地震作用下，对该工程实例双柱墩墩顶位移进行验算，纵桥向墩顶位移为1.43 cm，横桥向墩顶位移为6.72 cm，均满足小于纵桥向和横桥向的墩顶容许位移。