深海平台复合单系泊缆形状和张力分析
,, , ,
(中国计量学院 计量测试工程学院,杭州 310018)
浮式生产存储系统(FPSO)不仅能满足浅海作业要求,同时也适合在深海海域生产。工作在浅水的海洋平台一般采用全锚链的系泊缆形式,如果在深海海域也采用锚链,系泊缆不仅提供的水平恢复力有限,而且缆绳自重的增加将大量消耗浮式平台的可变载荷,因此在深水中主要采用多成分的系泊缆,即靠近海底和接近浮式海洋平台的部分使用锚链,中间的部分采用其他材质的缆索。最常用的是“锚链-钢缆-锚链”的组成形式。随着油气开采进入超水深和新材料在海洋工程中的使用,现在开始采用“锚链-合成纤维绳-锚链”的组成形式,这样既可以减轻自身的重量,又能提供足够的水平恢复力[1]。
目前基于系泊系统静力分析的应用程序很多,这些程序能求解锚泊系统的受力和变形,其计算过程一般需采用多次迭代的方法,最终找到锚链顶端受力与锚链顶端的位置,一般比较耗时[2]。
本文提出一种较为简单快速的求解锚泊系统静力形状和张力特性的方法[3-5],并且完成一次计算所耗时间不到1 s,特别适应于需要多次迭代计算的复杂系泊系统静力特性的等效水深截断系统优化设计[6-8],主要针对水平模态的系泊系统,亦即悬链线模态或松弛模态(有剩余索链躺在水底的)。
1 复合单缆系统静力计算
实际系泊系统中,各分段材质一般不同,各分段连接处也可通过悬挂重物或具有定常浮力的水下浮标连接起来。缆索在水中的重量可能为正,也可能为负或零。同时应考虑各分段的弹性拉伸(线性或非线性拉伸)。
图1为分析所用的系泊系统简图。建立总坐标系xoz,水深为h。设缆索分成N段(N>1),第一段下端与锚连接,第N段上端与浮体相连。以各分段(如第i分段)的下端为原点取局部坐标系xiozi,坐标轴均与总体坐标轴平行。
当wi≠0缆索未拉伸时,将第i段的水平跨距和垂直跨距分别记为xi和zi,若把该缆索分段近锚端的垂向张力记作Li,向下为正,近浮体端的垂向张力记作Ui,向上为正,设Th为缆索的水平张力,在整条缆索上为常数,则该段的悬线方程为
(1)
当wi=0缆索未拉伸时,分段成直线,xi和zi可写成
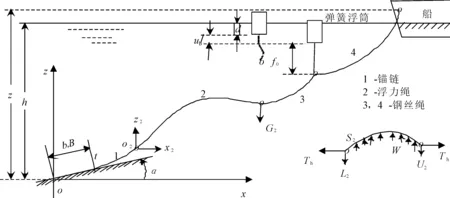
图1 系泊系统及坐标系
(2)
如图1所示,记缆索与海底的接触点为t,则海底上缆索的未拉伸长度记为
(3)
分段i的端部的垂向力可由点i沿缆索向上将缆索重量相加得到,即
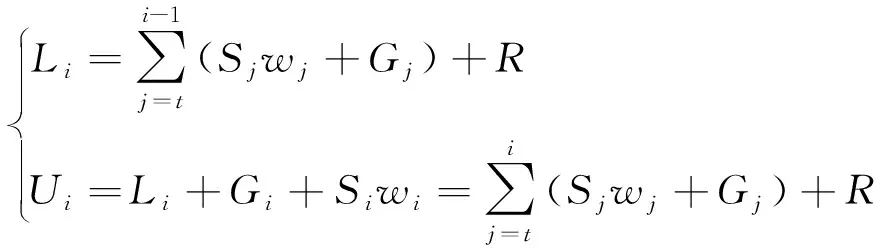
(4)
式中:R——锚固点上的垂向反作用力,
R=Thtanα,R>0表示缆索松弛。
其中:α——海底倾斜角,若海底水平,则R=0。
考虑缆索的弹性拉伸,可对上述方程中缆索的特征量进行修正,有
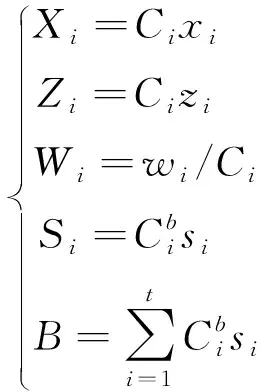
(5)
式中:Xi,Zi,Wi,Si和B——xi,zi,wi,si和b在拉伸后的值;
Ci——分段拉伸后长度与未拉伸长度之比为拉伸系数;

此外,浮躁的社会氛围对初中生读书的影响还表现为手机、网络等视听媒介对学生的强大吸引力。游戏和聊天成了学生的常态,这种现象在农村初中生身上尤为明显。因为大多数家长常年外出打工赚钱,自控能力不好的学生便会以电视、游戏作为自己在家的主要内容,影视文化、网络文化代替了课外阅读,使得学生对纸质书阅读兴趣大大降低,并导致思维简单化、平面化,思考能力和创新质疑能力减退。
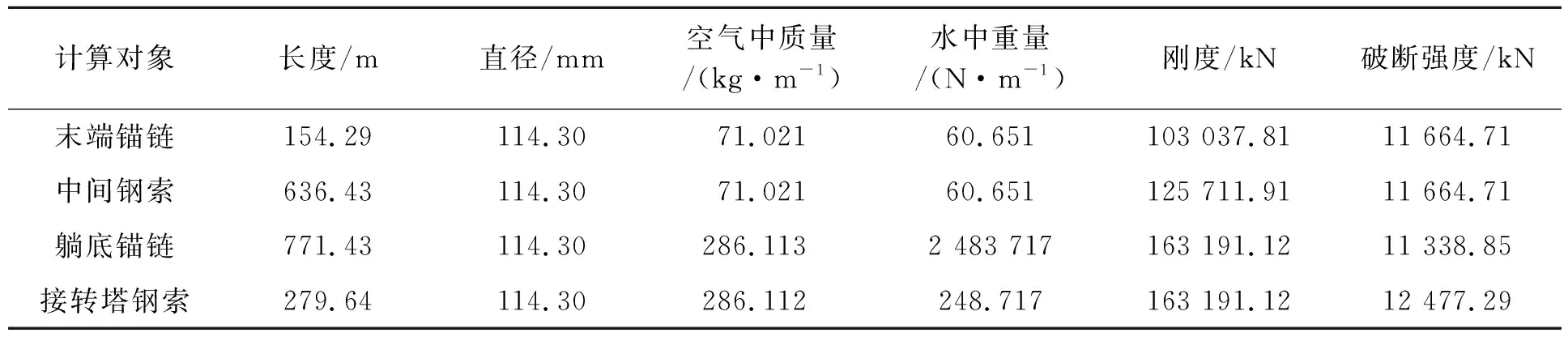
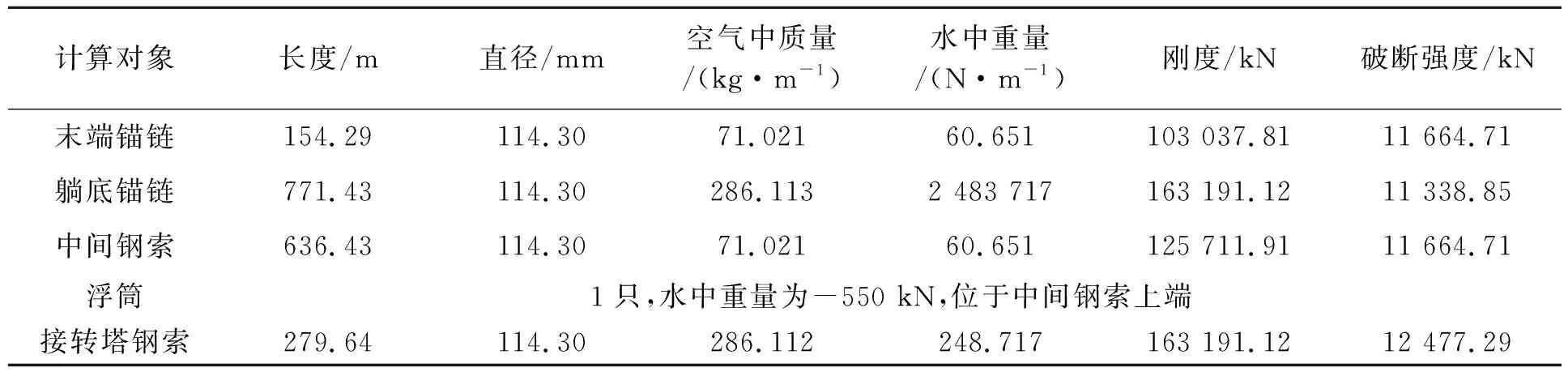
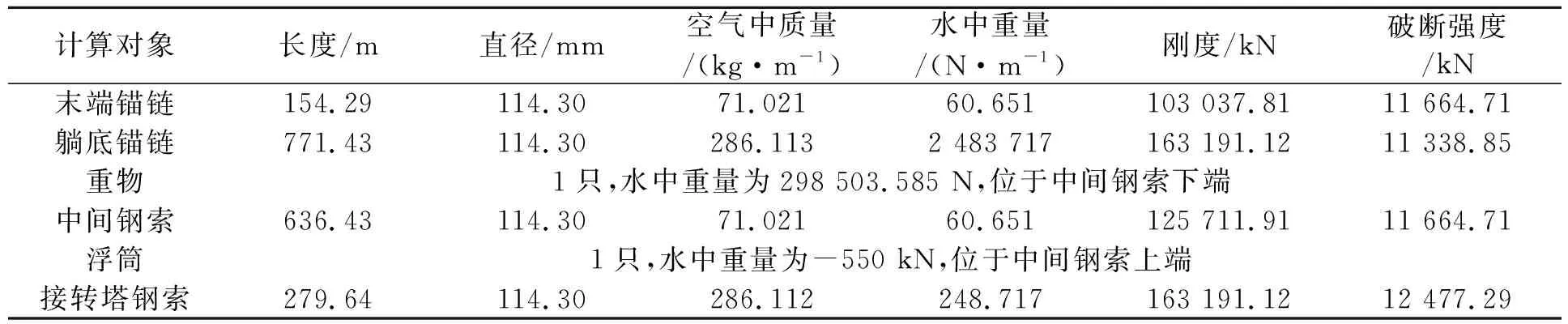
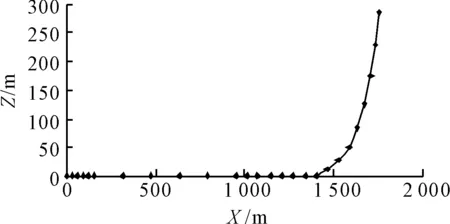
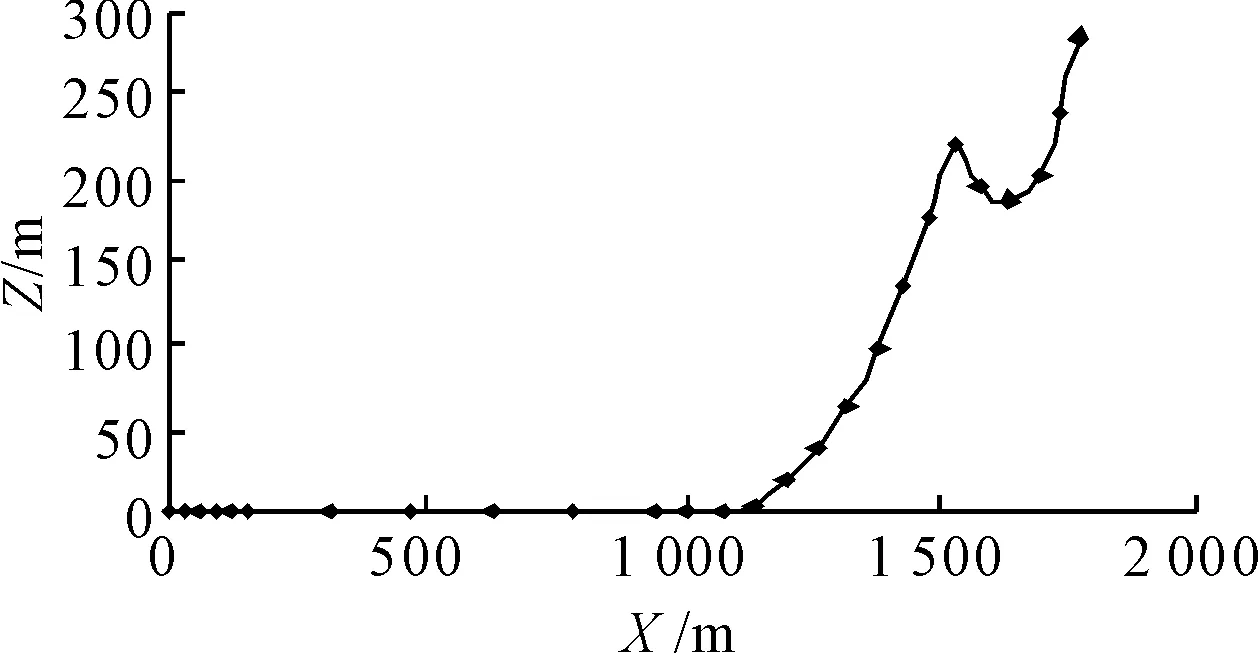
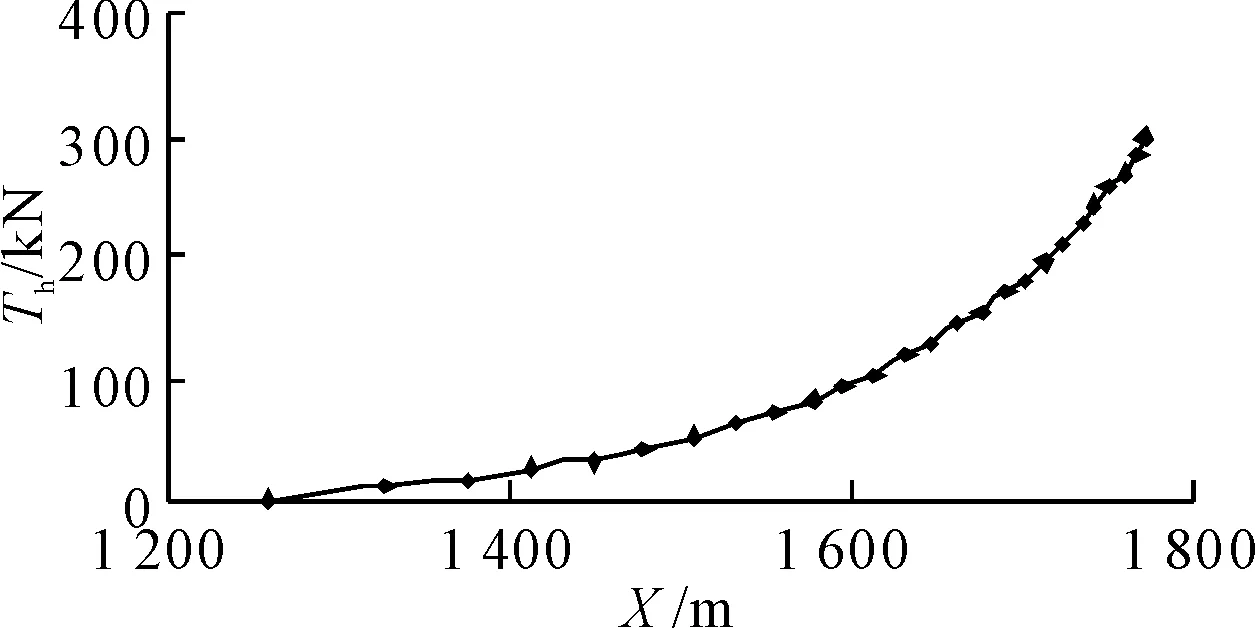
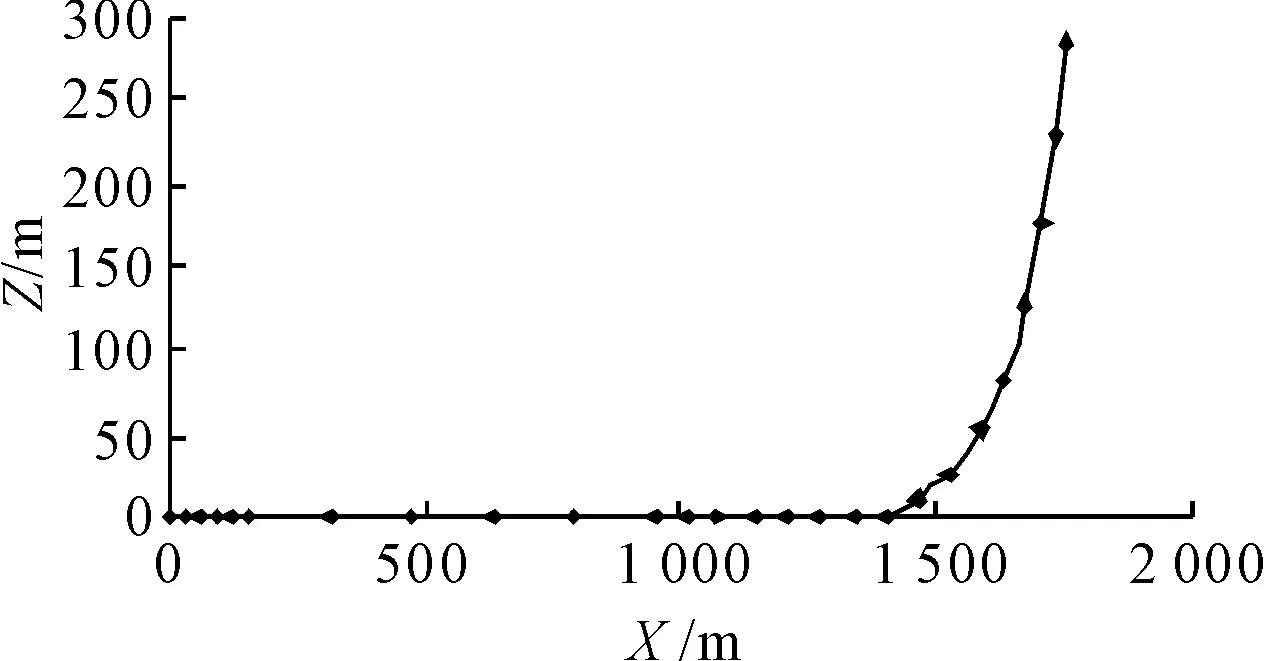
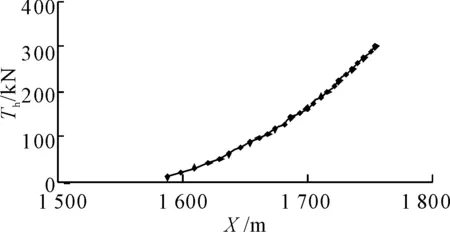
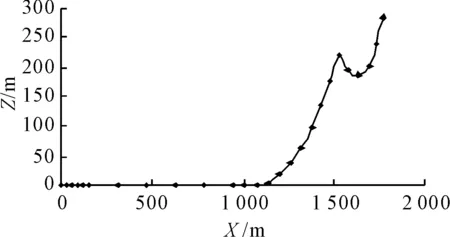
如果第K段缆索分段的顶端(1 (6) 和 (7) 式中水面浮标的吃水增加db为 (8) 式中:d——自由漂浮时水面浮标的吃水; f0——浮标底部与第K缆索分段顶端的垂直距离(见图1),f0>0。 缆索总的跨距为 (9) 水平系泊模态缆索系统平衡时的评价函数将是(缆索要求的垂向跨距为Z1,已知) (10) 迭代过程是先对于较小的Th值设定足够大的b值,使式(10)成立,改变b值,直到精度满足要求,当Th增大到一定的值时,b=0,R成为迭代变量。由不同的Th未变量的函数可得到水平跨距Xi、垂直跨距Zi、躺底锚链的长度B、缆索上端的总张力T、顶端夹角θ、系泊点处系泊缆与海底夹角α、系泊点处垂向张力Tv。 基于上述理论,采用C++编写系泊系统静力计算模块,基本思路是选取黄金分割法和悬链线方程计算出每种类型锚泊线的水平张力Th-水平跨距X曲线,以离散点的形式给出;然后依次给出上端系缆点水平移动距离,相应的计算单根锚泊线新的水平跨距。 以文献[4]中的算例为例验证系泊系统静力计算模块的准确性。缆索上端与船舶相连,连接点恰好在水面上,缆索水中重为828 N/m,断破强度为1 510 kN,水深25 m,缆长100 m。对比原文计算和本文计算的水平张力Th-水平跨距X曲线结果见图2。可以发现本文计算的结果曲线更光滑一些,因此本文所编写的静力计算模块准确度比较高,可以用于系泊缆的静力分析。 图2 系泊系统静力计算模块验证 以一系泊于310 m水深的FPSO为例,定常吃水,定常排水。悬链式系泊缆长1 841 m,浮筒位于中间钢索上端,重物位于中间钢索下端,系缆组成见表1~4。两种系泊系统预张力水平分量Th均取为300 kN。 表1 310 m水深系泊缆主要参数与属性(无浮筒重物) 表2 310 m水深系泊缆主要参数与属性(只有浮筒) 表3 310 m水深系泊缆主要参数与属性(只有重物) 表4 310 m水深系泊缆主要参数与属性(有浮筒和重物) 图3、5、7和9为无浮筒重物时、只有浮筒时、只有重物时及即有浮筒又有重物时的缆索形状曲线图;图4、6、8和10为它们对应的水平张力Th-水平跨距Xt曲线。 图3 无浮筒重物缆索形状变化 图4 无浮筒重物张力-水平跨距变化 图5 只有浮筒缆索形状变化 图6 只有浮筒张力-水平跨距变化 图7 只有重物缆索形状变化 图8 只有重物张力-水平跨距变化 图9 有浮筒重物缆索形状变化 图10 有浮筒重物张力-水平跨距变化 310 m水深系泊系统静力特性计算时选取的控制参数如下:允许垂直跨距计算值与要求值误差精度εz为0.001;允许水平张力计算值与要求值误差精度eTh=0.001;需要输出的X-T(水平位移-锚泊线张力)离散点数PnXe为26;水平位移增量间隔ΔX(m)为-2.0;设定海底上缆索未拉伸前长度范围b0LH(m)初始值为[0.1,2 000];初始给定的水平张力范围Th0LH(N)为[10,3 000 000];从海底锚固点到系缆桩缆索各材质分段的局部计算分段数CssN依次取为5、5、10和5;计算时取均匀流速为0 m/s,纵荡偏移范围取为-50 m,步长取-2 m,从0开始计算到-50 m,共26个点。 本次计算共耗时不到1 s,消耗机时与水深和锚泊线长度有直接的关系,水深越深,锚泊线越长,计算时需要处理的计算分段数越多,相应的时间也会越长。 在分析静力计算的基础上,编写了基于Visual C++的静力计算程序求解多成分系泊系统静力特性,主要适用于松弛的(有剩余索链躺在水底的)系泊状态,本文方法比较简单直观,容易理解,并且耗时很短,特别适合于需要多次迭代计算复杂系泊系统静力特性的等效水深截断系统优化设计,为动力特性研究的基础。 [1] 唐友刚,张素侠,张若瑜,等.深海系泊系统动力特性研究进展[J].海洋工程,2008:26(1):120-126. [2] 张火明,范 菊,杨建民.深水系泊系统静力特性快速计算方法研究[J].船海工程,2007,36(2):64-68. [3] OPPENHEIM B W,WILSON P A.Static-2d solution of a mooring line of arbitrary composition in the vertical and horizontal operating modes[J] .International Shipbuilding Progress ,1982(29):142-153. [4] 缪国平.挠性部件力学导论[M].上海:上海交通大学出版社,1996. [5] 张火明,张晓菲,杨建民.基于优化思想的多成分系泊缆静力特性分析[J].舰船科学技术,2010,32(10):114-121. [6] 苏一华,杨建民,肖龙飞,等.基于静力相似的水深截断系泊系统多目标优化设计[J].中国海洋平台,2008,23(1):14-19. [7] 张火明,杨建民,肖龙飞.混合模型试验等效水深截断系统优化设计研究[J].海洋工程,2006,24(2):7-13,20. [8] ZHANG Huo-ming,SUN Zhilin,YANG Jian-min,et al.Investigation on optimization design of equivalent water depth truncated mooring system[J].Science in China Series G,2009,52(2):277-292.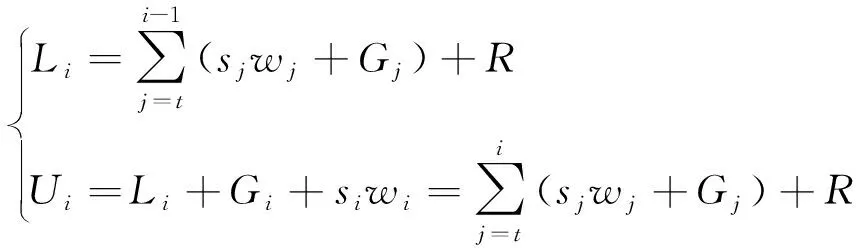
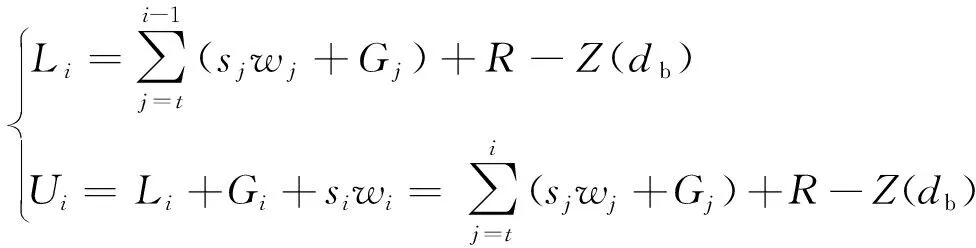
2 复合单缆系统静力特性计算方法
3 算法验证

4 算例分析



5 结论

