典型船舶焊接接头应力集中系数有限元分析

(南通中远川崎船舶工程有限公司,江苏 南通 226005)

焊接部位是结构强度的薄弱环节，通常被简化为各种类型的焊接接头。最常见的焊接接头形式有对接接头、T 形接头等。焊接接头的焊趾处由于结构形状的连续性受到破坏和材质不均匀性而引起的应力集中，是导致焊接结构断裂和疲劳破坏的重要原因。因此，研究焊接接头几何参数对焊趾处的应力集中系数的影响，对于准确计算焊趾处的应力分布，分析疲劳强度，提高疲劳寿命预测精度有重要的意义。目前对焊接接头应力集中系数的计算公式准确性不够，实用范围较小。本文利用MSC/PATRAN软件建立有限元分析模型，并利用MSC/NASTRAN进行计算。通过对影响应力集中系数的几个重要几何参数的改变，计算出多组应力集中系数[1]；对计算结果数据进行系统分析，研究应力集中系数Kt随几何参数的变化趋势，在此基础上回归出应力集中系数Kt的计算公式。

1 对接接头的简化处理

对接接头是船舶与海洋工程结构中常见的焊接接头形式。对接接头由焊缝金属、熔合区、热影响区和邻近的母材所组成；焊接接头中的化学成分、金相组织和力学性能一般是不均匀的。对接接头的疲劳强度在很大范围内变化，这是因为有一系列因素影响对接接头的疲劳性能[2]。本文将对接接头简化为平面问题。对接接头常见的坡口形式有两种,见图1。

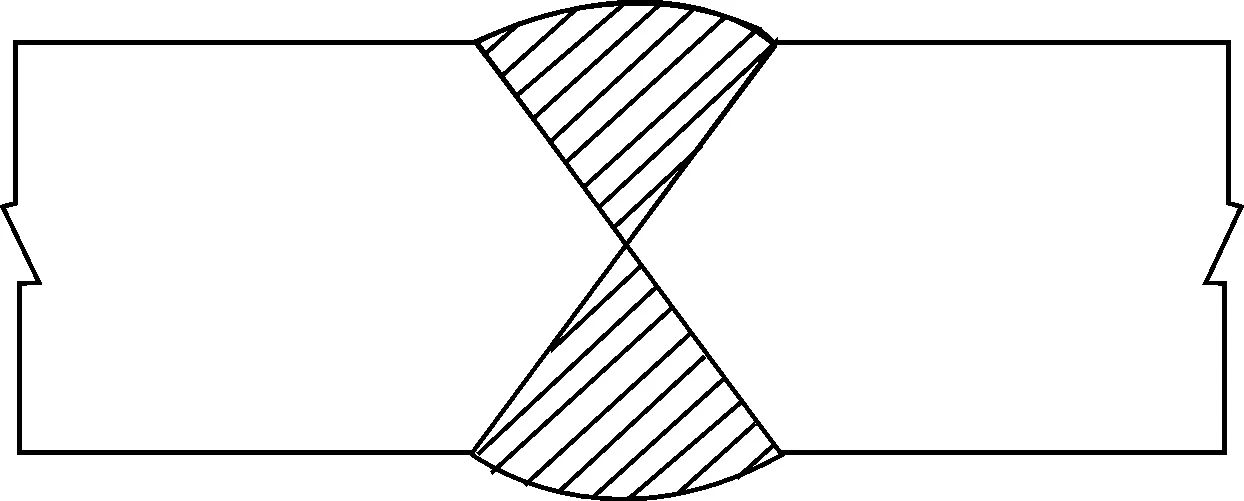
a)单侧加强高对接接头

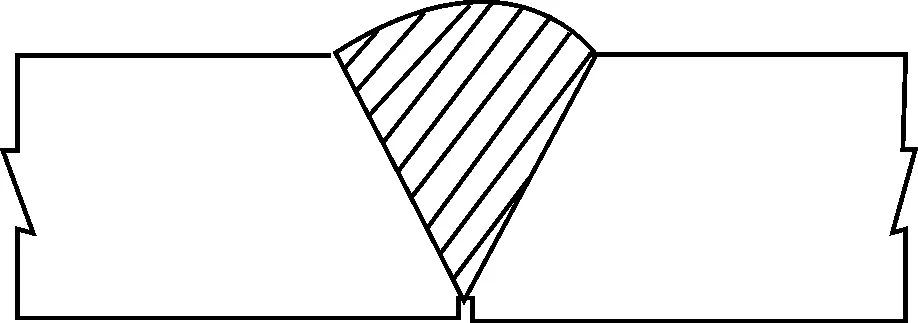
b)双侧对称加强高对接接头

2 建立模型并进行分析计算

考察几何参数对于应力集中系数Kt的影响，选取几何参数取值范围，只对单侧加强高对接接头进行研究。影响接头应力集中系数的因素很多，如焊趾倾角、焊趾过渡圆弧半径、板厚、焊缝加强高、焊缝宽度等[3]。假定不存在残余应力和其它焊接缺陷，选取主要几何参数(θ、r、t)，见图2。θ为焊趾倾角，r为焊趾过渡圆弧半径，t为板厚。

网格划分的最小单元尺寸为0.09 mm，材料弹性模量E=2.1 GPa,焊件的板厚t取20 mm，载荷为均匀拉伸载荷，在平面应变条件下进行计算。因对称性，模型以焊缝中心截面为对称面，取一半进行计算。为能较全面地考察几何参数θ、r、t对焊趾处应力集中系数Kt的影响，参数取值范围见表1。

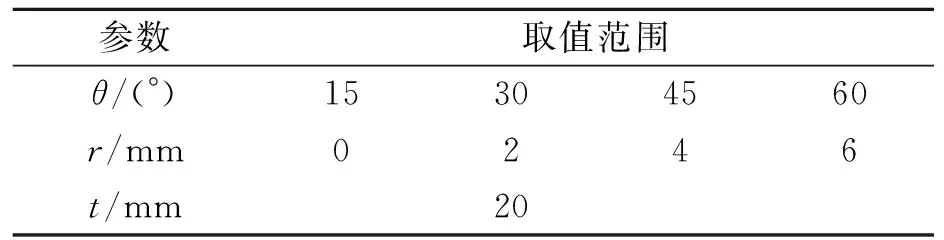
表1 几何参数取值范围

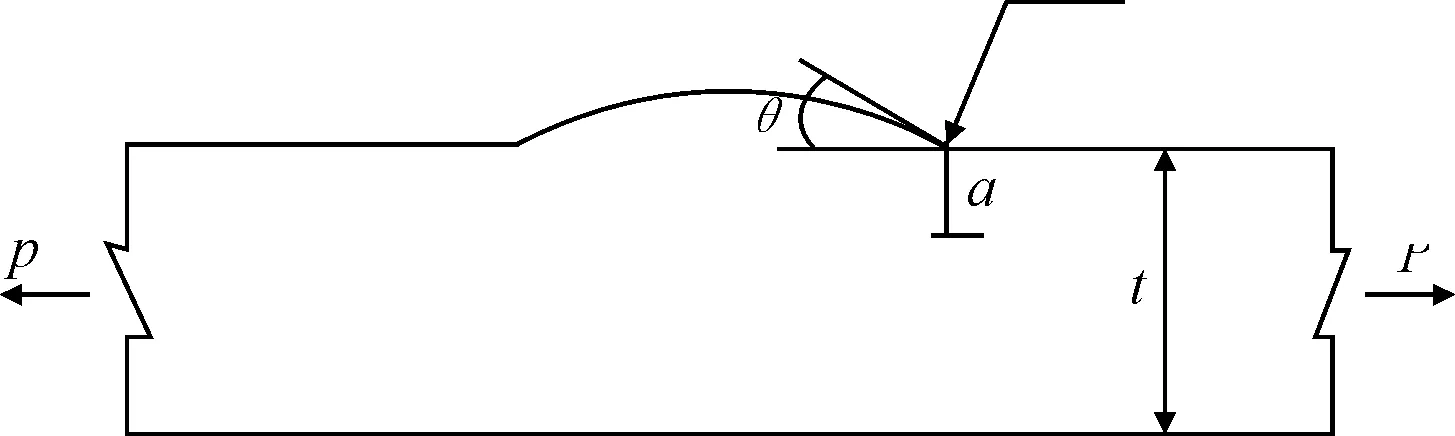
图2 有限元计算模型

3 计算结果及分析

r=0,θ=15°,t=20 mm 时，先用MSC/Patran建立对接接头焊趾处网格划分图(见图3)；然后，利用MSC/Nastran进行分析计算，计算结果见图4。

图3 网格划分(r=0，θ=15°)

图4 计算结果(r=0，θ=15°)

网格的一侧为刚性固定，另一侧施加固定载荷100 N。

由图4可知，最大应力σm=173 MPa，基准应力σ0=100 MPa。

由公式

(1)

得应力集中系数Kt=1.73。

在相同的网格单元及同样的载荷情况下得到单侧对称加强高对接接头模型有限元计算结果，板厚t不变(t=20 mm),Kt随焊趾过渡圆弧r和焊趾倾角θ的变化情况见表2。

表2 r和θ对Kt的影响

1)r对于Kt影响较大。由于过渡圆弧的存在，使得焊趾处的截面变化缓和，所受应力值减小；在总外力不变的情况下，Kt相应下降。总体上，Kt随r的增大而逐渐减小。但r较小时，Kt减小的幅度较大，作用较明显；随着r的增大，这种Kt的减小趋势变弱，作用逐渐减弱。

在θ=30°时，r从0～2 mm，Kt由1.83减小到1.51，减小了17.5%；r从4～6 mm，Kt由1.37减小到1.29，只减小了5.8%，变化幅度很小。

当θ=60°时，r从0～2 mm，Kt由2.04减小到1.55，减小了24.0%；r从4～6 mm，Kt由1.37减小到1.28，只减小了6.6%。

同样，θ=15°，45°时，所得结论也大体相同。

当r达到一定值时，Kt减小的幅度会很小，变化不太明显。

2)θ对应力集中系数Kt的影响。θ=15°时，r从0～6 mm，Kt由1.73减小到1.35，减小了22.0%；

θ=30°时，r从0～6 mm，Kt减少了29.5%；

θ=45°时，r从0～6 mm，Kt减少了34.0%；θ=60°时，r从0～6 mm，Kt减少了37.3%。

由此得出，θ取值越大，r从0.2～6.0 mm，Kt减小的幅度越大，而r>2 mm时，应力集中系数Kt随θ的增大，变化不明显，趋向于稳定。这是因为，随着θ的增大，引起接头焊趾处的截面变化加剧，增加了应力集中，从而导致Kt增加。但是r大到一定程度时，则不再如此。

r=0时，θ从15°～60°，Kt由1.73增加到2.04，增幅17.9%，较明显；

当r=4 mm时，Kt由1.39减小到1.37，变化了1.3%，幅度甚微。

3)在计算分析的基础上回归出计算公式。根据已有的数据和曲线形状特性，用统计的方法对影响Kt的几何因数进行回归分析，得出回归公式：

Kt=1+r-0.6sin0.2θ，0≤r≤6

(2)

因为假设厚度t为定值(20 mm)，所以公式中未考虑t的影响。

式(2)是在表2数据基础上，通过公式拟合、回归所得，在一定的范围内具有较高的精度。

4 结论

1)焊接接头几何参数对于焊趾应力集中有着重要的影响，随着接头形式、外载荷形式等因素的变化，影响程度有所不同[4]。对其影响规律做比较系统的阐述，对提高接头的设计工艺，改善焊趾应力集中有实际意义。

2)本文给出计算应力集中系数公式的参数，取值范围是参考已有文献而取的，基本上涵盖了船舶与海洋工程结构物中焊接接头的相应参数值，在该领域中有一定的实用意义。

3)应力集中区域单元网格的划分，在整个计算过程中占据了重要的地位。焊趾处单元网格尺寸微小的变化都可能引起计算结果较大的差异。

本文在建模过程中，先进行模型试验，不断对网格细化，发现当网格最小单元达到0.09 mm时，不管网格再怎么细化应力系数值都保持不变。依此，本文所有的网格均以0.09 mm为最小单元来进行划分，网格划分是合理的。

[1] 张 毅，黄小平，崔为成，等.对接接头焊趾应力集中有限元分析[J].船舶力学:2004,8(5)12-15.

[2] 齐 辉.电测法测定压力容器应力集中系数[J].辽宁化工.2003,32(12):9-11.

[3] 于有生，卢 伟.对接接头工作应力分布及其应力集中系数的研究[J].武汉理工大学学报，2005,29(1):25-28.

[4] 佐藤邦言.坡口形状、板厚、焊缝厚度、焊根角度对焊缝根部应力集中系数的影响[J].国外焊接技术，1980(3):12-17.