船行波对直立岸壁的作用研究

，

(武汉理工大学 交通学院,武汉 430063)

1 浅水条件下船舶兴波计算

船舶兴波阻力计算采用的面元法可分为两类，按照所采用的格林函数不同，分别为Rankine源方法和Kelvin 源方法(又称Havelock源方法)。

采用Rankine源格林函数，在整个流场边界布置源汇。在船体表面及部分自由面进行源汇分布，设船体表面S上的源强为σs(q)(这里是汇)，其所诱导的速度势为

(1)

设自由面F上的源强为σf(q)，其所诱导的速度势为

(2)

则总得速度势为

φ(p)=φs(p)+φf(p)

(3)

为求解速度势式(3)，必须求解边界面上的源强σ。一阶Rankine面元法的思想是采用一定数量的四边形或三角形小平面(即面元)代替连续的船体曲面及自由面(以及其它边界面)。假定每片面元上的源强为常数σi(q)，则可得到离散形式的速度势。

将船体曲面S离散为Ns片面元，记第i片面元上Si的源强为σs(i)，则式(1)转化为

(4)

同理，将自由面F共离散为Nf片面元，则式(2)转化为

(5)

将离散后的总速度势表达式分别代入各个定解条件，并在每片面元上选取一个满足当地约束方程的场点P(称为配置点)，可得到总共Ns+Nf个线性方程。求解方程组，求得每个配置点所在面元的源强，从而解决问题。

Wigley船船型要素：船长L=8 m，型宽B=0.8 m，吃水T=0.5 m，Wigley单体船在深水中航行时不同Fr数下的兴波阻力系数曲线见图1。与实验结果比较，结果令人满意。

图1 Wigley单体船兴波阻力系数

用面元法计算Wigley船型双体船和三体船浅水的近域波形。计算的船型：Wigley双体船，两片体中纵剖面之间的距离分别为0.2L，0.3L，0.4L和0.5L。对于三体船，不同的侧体排水量，不同的横向和纵向间距，对其阻力都有极大的影响。本文Wigley三体船，以Wigley单体船为主体，侧体排水量取主体的0.125倍，横向间距分别为Ys=0.2L，Ys=0.3L,Ys=0.4L，Ys=0.5L，纵向间距Xs=0，得到的波高数据见图2、3。

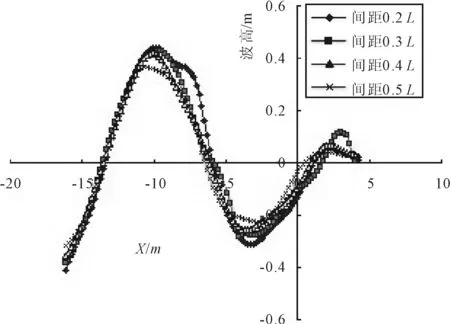
图2 Wigley双体船不同间距下船侧0.3L处波高

图3 Wigley三体船不同横向间距下船侧0.3L处波高

由以上波高图形可以看出，对于Wigley双体船和三体船，与在深水情况下相同，由于片体之间波系存在相互干扰，当片体与片体或片体与主体之间的间距越小时，其造成的兴波越大，在干扰发生的船艉附近尤为明显，见表1。

表1 浅水波高计算结果

2 船行波对直立建筑物的作用

《海港水文规范》(JTJ213-98)[1]第八章有如下规定。

当d1≥0.6H时，图4所示的直墙建筑物上近破波的波浪力按下列规定确定。

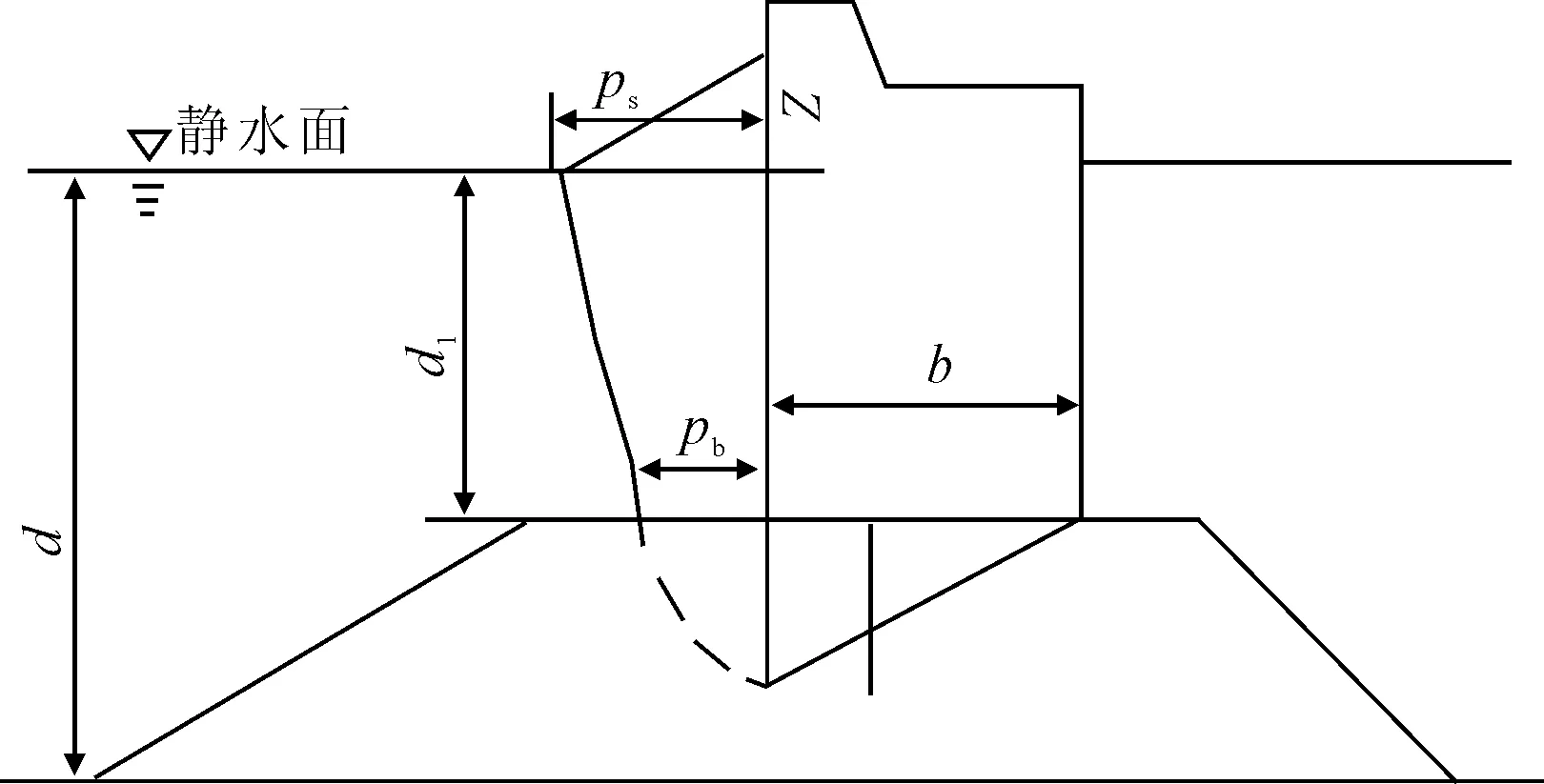
d-建筑物前水深，m；d1-基床上水深，m；Z-静水面以上高度， m；ps-静水面处的波浪压力，kPa；pb-墙底处的波浪压力，kPa。

图4近破波的波压力分布

1)静水面以上高度Z(m)处的波浪力为零，Z按下式计算。

2)静水面处的波浪压力按下列公式计算。

3)墙底处的波浪压力按下式计算。

pb=0.6ps

4)单位长度墙身上的总波浪力按下列公式计算。

3 计算分析

至今对直墙建筑的破波波浪力还不能以严密的理论进行分析计算，在工程上只能采用经验方法，而经验公式中的波浪要素均为粗略的估算，本文则利用船舶兴波的数值计算，以数值计算得到的较为准确的波形为输入波，利用经验公式计算波浪力，将船行波的数值计算与波浪对岸壁的作用相结合起来计算波浪力。

本文对于近破波的计算，基床底水深d取1.28 m，堤脚水深d1取0.48 m，将在浅水条件下Wigley各种船体船侧0.3L处的近域波高数据代入《海港水文规范》(JTJ213-98)公式计算得到船舶兴波对直立建筑的波浪力数据，见表2。

表2 波浪力计算结果

由表2得到的压力见图5、6，纵坐标为直墙建筑物各点位置，横坐标为该点处的波压力。

可以看出，当间距较小时，双体船和三体船船波对直立建筑物的近破波波浪力较大；随着间距的增大，双体船造成的波浪力逐渐减小。可见无论是对双体船还是三体船，间距的影响还是很明显的。由于缺少有关实验资料，无法比较用船波数据计算得到的值与实际值相差多少，这种方法计算的波浪力的准确性尚需进一步检验与讨论。

图5 双体船近破波的波压力

图6 三体船近破波的波压力

4 结论

采用一阶Rankine源面元法对浅水Wigley双体船和三体船的近域波形进行数值计算，并以其结果为输入波计算了船行波对直立建筑物的近破波波浪力，结果表明该方法具有一定的可行性[2-4]，其准确性还有待进一步验证。

[1] 交通部.JTJ213-98海港水文规范[S].北京：人民交通出版社,1998.

[2] 张 伟.高速排水型船舶兴波波形及尾浪的数值计算[D].武汉：武汉理工大学，2009.

[3] 屈晓婷.破碎波对直立建筑物作用机理的实验研究 [D].大连：大连理工大学，2008.

[4] 高 高.船舶兴波问题面元法计算中自由面离散的稳定性分析[J].水动力学研究与进展：A辑,2002(1)：53-60.