人体足踝部有限元模型的建立及有效性分析

吴恺杨茂伟*都承斐

（1.中国医科大学附属第一医院骨科，沈阳110001；2.北京航空航天大学生物与医学工程学院，北京100191）

随着工业、矿业及交通运输业的发展，足踝部的损伤不断增加，越来越受到骨科医师及运动医学专家的重视，人们对足踝部的生物力学研究也不断深入。活体组织研究能得到较为精确的数据，但因伦理学的原因受到限制，而对足踝部的传统研究方法是进行尸体标本的生物力学研究。尸体标本生物力学研究目前被认为是金标准，但也有其局限性，首先很难获得尸体标本；其次尸体标本生物力学研究只能获得标本模型的整体信息，标本模型内部的区域性力学特性却很难获得；再次，尸体标本模型失去随意肌的控制，与足踝部的自然状态也存在差别；此外模型的制备及测量也存在一定误差。随着计算机技术和有限元理论的不断发展，人们开始大量使用数字模型和有限元法分析复杂的结构。与以往的生物力学实验相比，有限元方法可以建立高度几何相似及物理相似的有限元模型，既可以反映区域性力学特性，又可以获得整体信息；既可以进行精确的数字分析，又可以进行形象的、直观的定性研究。本研究基于CT数据建立具有高度几何相似性的足踝部三维有限元模型，并对其有效性进行验证，为临床及生物力学研究提供新的研究手段。

1 资料与方法

1. 1 数据收集

男性志愿者1名，28岁，身高172 cm，体重60 kg，足部无外伤史，X线检查排除足部肿瘤、畸形等病变。采用中国医科大学附属第一医院影像中心的Brilliance 64排iCT，扫描参数：电压120 kV，电流强度372.5 mA，螺距0.297，层厚0.625 mm，矩阵512×512，曝光时间0.4 s/r，重建层厚0.9 mm，重建方法B+YC，重建间隔0.45 mm。对志愿者右足自踝关节上10 cm胫腓骨远端向下扫描至足底，扫描时右足保持中立位，共获得足部横断面CT图片516张，以DICOM格式存贮，刻录成光盘。

1. 2 有限元模型建立

CT扫描的数据导入三维重建软件Mimics10.0，通过阈值分开骨组织及软组织，建立足踝部骨骼几何模型；根据解剖图谱[1]及文献[2]在骨骼间的相应附着点建立韧带模型，骨骼以STL格式输出，韧带以IGES格式输出。然后将骨骼导入计算机辅助设计软件Geomagic Studio10.0中，对模型进行除噪点、平滑，根据各关节面的几何形状，利用软件加厚功能在各骨面生成关节软骨，最后拟合曲面，骨骼及关节软骨以IGES格式输出。将骨骼、关节软骨及韧带导入Ansys 13.0的Workbench模块进行材料赋值、网格划分、设置边界条件等处理，最后进行计算分析（图1）。

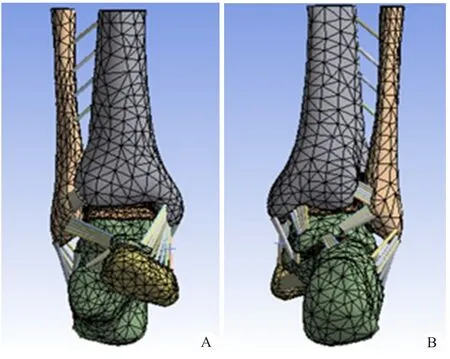
图1 足踝有限元模型

1. 3 材料参数

骨性结构和软骨均模拟为各向同性的线弹性材料，韧带使用只承受拉应力单轴梁单元来模拟。骨、软骨、韧带的材料属性由参考文献[3,4]确定，见表1。

表1 材料属性

1. 4 划分网格

1. 5 设置边界条件

本研究所建立的软骨较厚，与骨骼有交叠现象，通过布尔运算减去交叠部分再和骨骼边界设置为“绑定（bonded）”，二者就紧密地结合为一体了。韧带与骨骼之间的接触也设置为绑定，但如果韧带与骨骼之间距离过大则无法绑定，调整韧带止点，使之与骨骼绑定可靠。关节软骨之间采用有摩擦的面面接触，软骨面的间隙＜0.1 mm，关节之间由于关节滑液的存在，使得其间摩擦力非常小，依据参考文献[5]设置摩擦系数为0.01，用以模拟关节软骨之间的滑动特性。

由于Workbench划分网格功能十分强大，故对骨骼、软骨网格的划分采用“自动生成网格（automatic）”即可，网格尺寸选择为“粗糙（coarse）”即可，这样划分的网格基本满意，且节点和单元数量不多，在保证计算精度的前提下，提高了计算的收敛速度。对线体网格的划分仍可采用自动生成网格功能，但划分的单元数量选择为“1”，这样每条韧带只用一个单元模拟，使得计算效果更好。

1. 6 有限元模型的验证

参照Anderson等[6]实验所设置的的边界条件，模拟人体站立状态下的力学传递，对模型胫、腓骨下端的上截面施加600 N垂直压缩载荷，固定跟骨，约束距骨，测量踝关节下关节面的接触应力、接触面积，并将结果与前者进行对照。同时测量踝关节周围主要韧带的位移（拉伸长度），对踝关节的生物力学反应进行自身验证。

2 结果

本研究建立的正常人足踝部三维有限元模型形态还原性好，重建效果较理想，能任意旋转，可获得详细、满意的三维信息。模型计算胫骨下关节面最大应力（3.74 MPa）及应力分布均与以往研究结果具有相似性[6,7]（图2、3，表2），认为模型有效。模型测得踝关节周围主要韧带的位移（拉伸长度）见图4，其中胫跟韧带位移最大（5.24 mm），胫舟韧带（5.04 mm）、跟腓韧带（2.05 mm）次之，下胫腓联合前韧带位移最小（1.92 mm）。

图2 Anderson等对两个踝关节胫骨下关节面在标本和有限元模型中分别测量的应力分布结果示意图

图3 本研究建立的有限元模型胫骨下关节面应力分布结果示意图

表2 胫骨下关节面应力分布对照

3 讨论

自从Courant于1943[8]年提出有限元概念以来，有限元理论及其应用得到了迅速的发展，人们开发了多种逆向工程软件和计算机辅助设计软件，并且不断更新软件功能，以弥补软件本身的局限性。同时，人们也尝试不同方法建模，研究不同材料的属性以及划分网格方法，探索不同的边界设置条件及加载方法，以达到更好的仿真效果。随着技术的不断更新，生物数字仿真学也在不断地进步，但是由于生物组织几何上的不规则以及非均匀性、各向异性、非线性的材料特性，并且与应变速率、加载历史等因素具有相关性，目前很难精确模拟。足踝部骨骼形态极不规则，数量多、体积小，关节多且曲面复杂，韧带、肌腱繁多，且具有复杂的运动学与动力学特性，给有限元建模及模拟带来更多的麻烦。

为了克服足踝部有限元分析的各种困难，本研究做了不同的尝试。首先，采用多条线体模拟韧带，在Mimics中利用软件辅助设计（MedCAD）功能，根据解剖图谱[1]及文献[2]在骨骼间生成多条线单元模拟韧带，避免了单一线体或弹簧模拟韧带产生的应力集中，也避免弹簧所需要的预加载。韧带以IGES格式输出，可反复导入有限元分析软件，避免调整模型时反复制备线体，减少了工作量。韧带使用只受拉不受压的单轴梁单元来模拟其特有的力学属性，使用一个单元对线体进行网格划分，在不影响计算结果的同时优化了收敛效果。

其次，在计算机辅助设计软件Geomagic中根据各关节面的几何形状，利用软件加厚功能在各骨面生成实体模拟关节软骨。生成的各软骨厚度均匀，构造曲面片时采用单层结构，这样在与对应的骨骼做布尔运算后不会产生畸形结构，网格划分时也不会产生不良单元。在Geomagic中可清晰查看软骨间的接触，调整软骨，使相邻软骨之间只接触而几乎无交叠现象（交叠＜0.1 mm），提高计算的收敛率和有效性。参考文献[5]设置关节间摩擦系数为0.01，用以模拟关节软骨之间的滑动特性，保证了关节的有效滑动，使其更接近自然关节的状态。

图4 踝关节周围主要韧带的位移

由于受逆向工程软件和计算机辅助软件自身局限性，加之建模中也会受原始影像资料精确程度、模型重建方法、网格划分水平、材料属性赋值、研究者经验和熟练程度等因素影响，有限元计算的结果可能会与力学模型结果之间存在差别。因此，建立的有限元模型需要进行有效性验证，一般是将其与力学数据直接比较。本模型计算中立位踝关节垂直加载应力主要分布于胫骨下关节面中部及前外侧，最大应力2.49～3.74 MPa。Anderson等[6]研究显示两具尸体标本模型胫骨下关节面最大应力为3.69 MPa和2.92 MPa，两个有限元模型胫骨下关节面最大应力为3.74 MPa和2.74 MPa。刘清华等[7]研究显示有限元模型胫骨下关节面最大应力为3.97 MPa。以上研究胫骨下关节面应力分布结果与本研究相似，说明本模型有效。

模型同时也测量了踝关节周围四条主要韧带的位移（拉伸长度）。从文献[9]可知，踝关节周围韧带位移与踝关节及距下关节有关。踝关节为屈戌关节，距骨体及滑车前宽后窄，负重时下胫腓关节有分离趋势，下胫腓联合前后韧带十分坚韧，能够限制此趋势，维持踝穴的稳定、进而维持踝关节的稳定，因此下胫腓联合前韧带位移很小，本文测得的下胫腓联合前韧带位移最小，亦证实如此。由于外踝较内踝较长并靠后，故踝轴向后下方成角，当人体中立位负重时，小腿有外翻趋势。距下关节的前、中、后三个关节绕同一单轴运动，类似一斜铰链，由后外下方斜向前内上方，其运动轴无论在正位或侧位均与矢状位相交为一定角度。由于这一斜轴关系，站立位负重时进一步加重小腿的外翻，同时小腿亦出现了轻微的内旋，Liacouras和Wayne[10]等研究及Marqueen[11]等研究模拟中立位负重均显示胫骨有0°～0.5°的内旋。因此外侧的跟腓韧带位移小于内侧韧带，胫跟韧带位移大于胫舟韧带。本文计算的踝关节周围四条主要韧带的位移符合踝关节的生物力学反应，进一步说明了本模型的有效性，可以用于临床及相应的生物力学研究。

目前对足踝部生物力学的研究虽然取得了很大的研究成果和进展，但仍然只是做近似的模仿。本研究基于CT序列图像，对建模方法进行了尝试和创新，建立正常人体足踝部三维有限元模型，较真实、准确地模拟了足踝部的解剖形态，同时具有良好的生物力学特性。不足之处在于对模型进行了简化，仅建立了后足模型，且未考虑到肌肉等动力性结构，以后的工作需要进一步研究，使其成为足踝部生物力学研究的更好平台。

[1]高士濂.实用解剖图谱.下肢分册.第2版.上海:上海科学技术出版社,2004:275-281.

[2]Inhauser CW,Siegler S,Udupa JK,et al.Subject-specific models of the hindfoot reveal a relationship between morphology and passive mechanical properties.J Biomech,2008,41(6):1341-1349.

[3]Cheung JT,Zhang M,Leung AK,et al.Three-dimensional finite element analysis of the foot during standing:a material sensitivity study.J Biomech,2005,38(5):1045-1054.

[4]Bandak FA,Tannous RE,Toridis T.On the development of an osseo-ligamentous finite element model of the human ankle joint.Int J Solids Struct,2001,38:1681-1697.

[5]Anderson DD,Goldsworthy JK,Shivanna K,et al.Intra-articular contact stress distributions at the ankle throughout stance phase-patient-specific finite element analysis as a metric of degenerationpropensity.Biomech Model Mechanobiol,2006,5(2-3):82-89.

[6]Anderson DD,Goldsworthy JK,Li W,et a1.Physical validation of a patient-specific contact finite element model of the ankle.J Biomech,2007,40(8):1662-1669.

[7]刘清华,余斌,金丹,等.正常人足踝部有限元模型的构建研究.中华创伤骨科杂志,2010,12(2):174-177.

[8]Courant R.Variational method for solution of problems of equilibrium and vibrations.Bull Am Math Soc,1943,49:1-23.

[9]郭世绂.骨科临床解剖学.泰安:山东科技出版社,2001:989.

[10]Liacouras PC,Wayne JS.Computational modeling to predict mechanical function of joints:application to the lower leg with simulation of two cadaver studies.J Biomech Eng,2007,129(6):811-817.

[11]Marqueen T,Owen J,Nicandri G,et a1.Comparison of the syndesmotic staple to the transsyndesmotic screw:a biomechanical study.FootAnkle Int,2005,26(3):224-230.