论振动体电动力学（Ⅲ）—共振隧道效应与引力量子化

王鼎聪

（中国石油化工股份有限公司抚顺石油化工研究院，辽宁抚顺113001）

牛顿利用开普勒定律发明了宏观物体间相互作用力－万有引力。由于不能解释瞬间作用的机制，爱因斯坦用广义相对论克服了牛顿万有引力超距作用的缺陷，但广义相对论又产生了一个新的问题，加速度，万有引力，时空弯曲的循环论证［1］。尽管如此，广义相对论仍然是解释宇宙大尺度物体相互作用的最好理论。为了寻求一种单一的超力（GUT），粒子物理学的标准模型发展了已经半个多世纪，已经取得了巨大成就［2］。广义相对论和量子理论是分别解释天文尺度和亚原子尺度两个世界的理论，将其统一就产生了量子场论（QFT）［3］。量子场论已经取得了巨大成就，但一些人为的修饰是物理实在所不能忍受的，重正化等修正使优美的数学出现了瑕疵［3］。

引力场的量子化一直是理论物理科学的研究热点，引力辐射的存在问题是当前引力论的中心问题之一。在普朗克区有量子化的观点［4］，弦理论［5－7］和黑洞理论都努力将引力进行量子化［8－9］。

本文是以共振场的观点［10－11］，提出了万有引力产生是由共振隧道效应所决定的观点，并用纳米粒子制备实验结果进行了验证。

1 实验部分

1.1 实验药品

六水合硝酸镍（质量分数98%），分析纯；九水合硝酸铝，分析纯；尿素，分析纯；聚异丁烯马来酸三乙醇胺酯，自制；去离子水，自制；150HVI（润滑油基础油），工业级。

1.2 所用仪器

日本生产JSM－6301F型扫描电镜，加速电压20kV，用于观察纳米自组装体的外貌及粒子的大小；荷兰生产TECNAI20型电子显微镜，最高放大倍数100万倍，用于观察纳米自组装体颗粒形貌和分散状况以及粒径大小及分布状况。

1.3 纳米粒子的制备

1.3.1 纳米氧化镍和纳米镍制备 在搅拌条件下，将950g六水合硝酸镍与184g尿素加热至80℃，加入至同等温度条件下的12.5g聚异丁烯马来酸三乙醇胺酯和37.5g的150HVI油的混合物中，形成超增溶胶团。在120℃密闭反应3h，反应产物水洗3次，120℃干燥，550℃焙烧4h，得到纳米氧化镍［12］。在300℃微反中，通入H2纳米氧化镍被氢气还原得到了纳米镍。

1.3.2 纳米氧化铝制备 在搅拌条件下，将950g九水合硝酸铝与238g尿素加热至80℃，加入至同等温度条件下的14.2g聚异丁烯马来酸三乙醇胺酯和43.7g的150HVI油的混合物中，形成超增溶胶团。在120℃密闭反应3h，反应产物，水洗3次，120℃干燥，550℃焙烧4h，得到纳米氧化铝［13］。

2 结果与讨论

2.1 纳米粒子及聚集体的外观形貌分析

图1（a）是Ni的纳米晶体，从图1（a）中可以看出，粒子直径在7～10nm。原子Ni电子的电离能为736eV，相应的电子普朗克能力能量相应波长极高，在微米级范围，波长远远大于原子半径的pm级别，波长与原子半径几乎没有任何相关性。

图1（b）是图1（a）中纳米Ni，自然堆积产生的二次纳米Ni粒子。从图1（b）中看出，二次粒子的直径在1μm左右，粒子间以稀松的堆积方式自然堆积，粒子颗粒间的空隙可以清晰可见。

图1（c）是一次纳米氧化铝堆积的二次粒子。由于铝原子价态是3价，可以与其它2价以上的原子形成立方的网状结构，所以粒子可以有多种形态。从图1（c）可以看出，粒子是以片状互相重叠，形成大量一次粒子堆积成一圆形的二次粒子，粒子直径约5μm。这些相互作用都是以原子半径键合成分子间力，作用范围是原子半径范围，也就是电子能够相互作用的区域，产生的力是电力范围。

图1（d）是大量二次氧化铝粒子在TEM的碳膜上分布，可以看出，二次粒子之间没有相互作用，二次粒子直径都在微米级范围。这些作用已经超出电子的作用范围。

Fig.1 TEM and SEM of nano nickel and nano－alumina图1 纳米镍和纳米氧化铝的SEM和TEM

2.2 电磁力及非电磁力的作用范围

Ni是如何形成结晶，现代原子形成用价键理论解释，晶体的形成与原子半径有关，原子半径是实验结果，但是价键理论中的解释是一种定性的描述，无法解释电子在原子中半径与分子键合的本质原因。

二次粒子的形成是一次粒子的互相吸引产生的，这个吸引力不是用原子中电子产生的静电力产生的，是由粒子间弱的相互作用力产生的。图1（d）二次粒子分布在样品台上，可以看出都是自然随机分布。这种自然随机的分布，可以看出粒子之间是没有电磁力的作用，没有电场力或磁场力产生的相吸或排斥作用，否则粒子将发生聚集。

从以上分析可以看出，一次纳米粒子是以原子半径为作用范围，产生的力是电子产生的力，也就是电力作用范围。而二次粒子直径在微米级范围的是远远超出原子半径，从图1（d）粒子分布来看，粒子间是没有电力或磁力的，表明了在微米级以上的都是非电磁力作用。

3 共振点与原子半径关系

3.1 共振点的宏观性与微观性

共振点既具有宏观性又具有微观性。普朗克能量E中电子共振点运行的轨道半径是与原子半径紧密相关的，由于原子间或分子间的距离是原子或分子的键长。很明显，普朗克能量E中非常高的波长与原子中电子在轨道中半径没有任何关系，是一个宏观量，这是共振点的积分值。这个宏观量是由电子绕质子的运动具有基本的共振点，共振点是以直线型在轨道上运动。电子基本共振点绕核2π周期运动一周，产生了具有波动性质的能量累加值—驻波能量值。电子的共振点绕核角动量轨道运动，电子的自旋角动量运动和电子自旋的进动运动三个微观运动，这三个微观运动是无法测量的，但是三者之和运动2π周期能量的积分总和，产生了普朗克公式的能量E＝hν，这个值是可以精确定量的。普朗克能量E看成是一个区间的基本共振点能量运动之和，这使普朗克能量E和非常高的波长转换成与原子半径相等的电子共振点在原子轨道中运动［11］。普朗克公式中的能量E及波长λ用电子的基本运动共振点累积来解释，是自洽的。

从分子键长看，如表1所示。原子鲍林共价半径和离子半径都是实验得出的结果，从表1中可以看出，原子的半径都在0.011～0.195nm，半径较小。分子键长和原子鲍林共价半径和离子半径数据，表明基本共振点是在此范围的。

表1 平均共振点半径（原子半径）Table 1 Average resonance point radius（atom radius）

续表1

定义1： 原子半径是原子共振点半径的平均值，具有电磁强相互作用，共振场相互作用具有短程力作用，必须满足内敛性原理。

无论红外光谱还是原子光谱相应的能量都是电子基本共振点累加的结果，则每个共振点两个电子产生的共振场必须是符合共振场的内敛性原理。如果这两个电子符合内敛性原理，则必须满足泡利不相容原理，也就是两个电子处于费米子的两个不同状态，时刻都保持相反的状态。

从以上分析得知，原子间相互作用只有在原子半径接触范围内，才能产生电磁力的作用。同理，共振场相互作用也是在共振点上，两个粒子辐射的相反场，产生了内敛性的相互作用，只有在共振点才会产生共振效应。

在均匀共沉淀纳米粒子形成过程中，如图2（a）所示，NiO纳米粒子形成是溶液中有大量的晶核，溶液中的Ni＋水合离子由于共振效应，水合离子向晶核聚集，在达到共振点的半径时，在内敛性作用下，水合离子与晶核共振距离内，两个相反共振场的离子结合形成NiO晶体的离子键。

Fig.2 TEM of nano nickel oxide crystal and secondary particles图2 纳米氧化镍一次晶体和二次粒子的TEM

图2（b）是多个一次纳米氧化镍晶体聚集成二次粒子，二次粒子约为1μm，从图中可以看出二次粒子结合的较为稀疏，粒子间结合不是电子绕质子的共振点半径产生的晶格分子键的作用，粒子都是独立，没有形成强的相互作用。

3.2 共振点与极化率

共振场相互作用具有短程力作用，而电力和磁力是长程力。共振点电子在原子绕核半径是有长短轴的，半径有长轴半径和短轴半径。原子的共价半径和离子半径是一个值，将原子半径定义为电子共振点半径，表示是电子共振点半径平均值的概念，实际共振点半径是变化的。共振点半径变化产生了分子的极化率。

分子振动能的E越大，对称性越低，极性越强。羟基的H－O极性大于双原子分子，这是由于双原子中原子与原子是相同原子，是完全的共振态，故是绝对对称结构，极性弱。而H－O极性强，对称性低，故极化率高。

4 共振势垒与共振势垒隧道效应

4.1 共振势垒

共振点之间发生共振效应，两个粒子产生了具有内敛性的共振场，形成了共振平衡稳定态，在两个稳定态之间跃迁交换的能量符合共振频率条件，即νa／νb＝i

i＝1／5，1／4，1／3，1／2，1，2，3，…，i时，粒子产生共振效应，如图3所示。

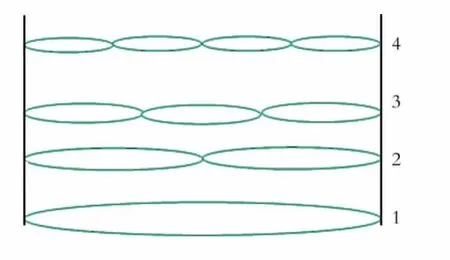
Fig.3 One－dimensional infinitely deep resonant potential well－resonance barrier图3 一维无限深共振势阱－共振势垒

将共振粒子放在一维无限深共振势阱中，来假设两个粒子的相互作用。一个粒子辐射的电磁场被另一个粒子能共振吸收，表示粒子发生了共振作用。若两个粒子发生共振，则在势阱中的粒子势能为零，表示两个粒子可以发生共振。在一维无限深共振势阱外粒子势能为无穷大，表示两个粒子没有相互作用

在阱内，吸收共振辐射的共振粒子，其粒子的动能应满足定态薛定谔方程

则方程可以改写为

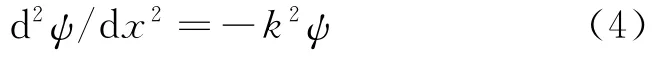
此方程的解为：

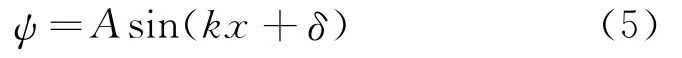
因为，在共振势阱外（0）＝0（阱外v（x）＝∞），波函数在x＝0，d处必为零，即得常数δ＝0。又因为ψ（d）＝0，即得量子化条件，kd＝nπ，n＝1，2，3，…。

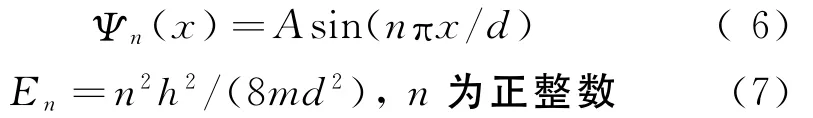
这就是共振势阱中粒子具有的能量，也就是共振态之间跃迁所具有的交换能量，这个能量是量子化的。

共振势阱中x区间的d值，就是两个粒子辐射电磁场不同共振态的共振波长，这个波长是普朗克能量相应的波长。

4.2 共振势垒隧道效应

对称一维无限深共振势阱模型中，共振势垒穿透问题与量子力学中方势垒穿透一致，即

一个粒子辐射的电磁场若能引起另一个粒子共振，当入射辐射具有的能量E与势垒内的共振能V0相符时，表示辐射的能量进入势垒引起了共振。在势阱中，若一个辐射引起能垒中一个粒子的共振，需要满足共振势阱壁间距为波长或波长的数倍才能产生，图4是共振势垒隧道效应模型。

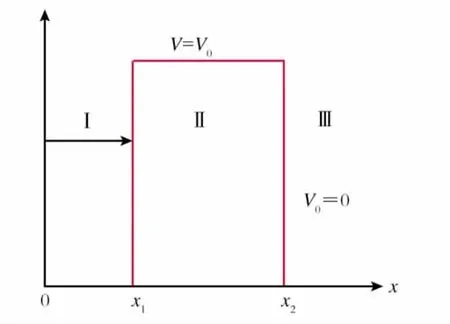
Fig.4 Model of resonance barrier on tunnel effect图4 共振势垒隧道效应模型

令一个粒子的能量为零点，则另一个粒子的能量还原为量子力学的波动方程形式。电子与质子的共振，若仅考虑电子能量，质子能量设为零点，则电子一维薛定谔波动方程为：

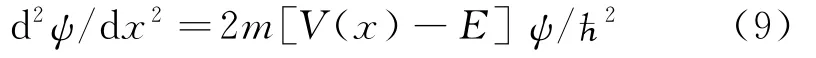
在区域Ⅰ，x＜x1，V＝0，方程变为，

其解为，

ψ1是一入射到电子上的电磁辐射。

在区域Ⅱ，x1＜x＜x2，V＝V0＞E，故方程为，

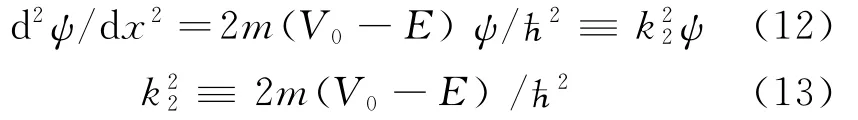
其解是指数函数，

解的含义是外部辐射到电子上的电磁辐射ψ0与电子的ψ2的形成了共振交集，只有满足ψ2的电磁辐射波长的倍数关系的ψ0才能被电子吸收，能使电子产生共振态的跃迁。

在区域Ⅲ，x＞x2，V＝0，

式中A2，B2，φ3均为常数，与A1，φ1一起可由波函数在x1，x2两点连续条件和归一化条件的要求决定。

由此可见，在区域Ⅲ的波函数并不为零，原区域Ⅰ的粒子有通过区域Ⅲ的可能。可以算出，粒子从Ⅰ到Ⅲ的共振穿透几率，

由此可见，共振势垒（D＝x2－x1）是来表示两个粒子产生的辐射拟合的程度。只有频率相同，粒子共振通过的几率越小，粒子的共振能量E越大，则共振穿透几率越小。因此，D和E的变化对共振穿透因子P十分灵敏。

4.3 共振势垒厚度因子D选择原则及相应的共振穿透几率

在量子力学中x2－x1是用厚度形象的比喻势垒的贯穿性，厚度越大穿透几率越小，但是x2－x1的物理意义是什么？量子力学并没有解释。这里，对D＝x2－x1给出共振场的物理意义。

现在，来考虑共振势垒厚度因子D的大小有什么影响因素及相应的共振穿透几率。共振势垒是一个电磁辐射能否使另一个粒子发生共振的能垒，势垒厚度因子D大小将决定该辐射能否使被激发的粒子产生共振跃迁能力。

共振势垒厚度因子D：共振势垒厚度因子D与共振相关系数成正比，与共振交集成正比，与共振波长和共振距离成反比。

共振频率的交集φ1∩φ2是共振场的共振程度的度量，两个频率完全相同电磁波能形成完全的共振态，频率差越大交集φ1∩φ2越小，共振程度越低。λ是粒子的共振波长，d是共振粒子间距离，a是共振半径r与共振距离d的相关系数，即a＝r／d，度量两个粒子相互作用的距离对D值的影响。

D值选择原则：

φ1∩φ2＝1，是表示相同的粒子的相互作用，可以分为两种情况：

（a）φ1∩φ2＝1，当r≅λ，d≅r时。这种情况出现在原子核内的质子相互作用。这时的共振点的半径与辐射的波长很接近，都在fm数量级。共振场的波长λ越小，频率越高，共振能量越高，这时能垒非常高，穿过高能垒几率越低，例如核子的能垒高于原子，原子的能垒高于分子。共振态的两个粒子相距距离d越近，只有波长距离表示，两个粒子是紧密接触的，从一个粒子中心到另一个粒子中心距离d就是波长λ，超过波长距离，距离越远，扰动越大，共振场的交集φ1∩φ2越小于1。

令a＝r／d≅1时，a≅1，则

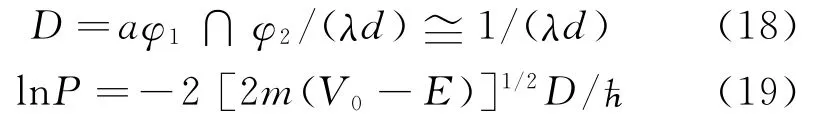
一个入射向共振体系的外来电磁辐射，波长为λ1，能量为，

质子和中子都是具有相同频率的粒子，作用距离与波长为相同数量级，P可以依据（16）得出。这个状态是共振态最稳定形式，称为完全共振态，是粒子间产生的最强相互作用力。P越小，共振态越稳定。

（b）φ1∩φ2＝1，当r≅λ，d≫λ时。

两粒子距离d对共振辐射的影响是最关键的因素。根据辐射能与平方成反比关系，d值越大，两者的φ1∩φ2越小。

当d≫λ时，将会导致φ1∩φ2→0。lnP＝－2k［2m（V0－E）］1／2D／ħ→0，P→1，粒子间是没有强相互作用的。例如质子距离超过一定距离后就没有强相互作用，在核物理中是核子普遍存在的现象。

（2）当φ1∩φ2→1时，r／d≪1时。两粒子距离d对共振辐射的影响是最关键的因素。根据辐射能与平方成反比关系，d值越大，两者的φ1∩φ2越小。

当d≫λ时，将会导致φ1∩φ2→0。lnP＝－2［2m（V0－E）］1／2D／ħ→0，P→1，粒子间导致没有强相互作用的。

如果，粒子是在液体中，粒子的相互作用将会出现两种情况。

a）如果初期形成晶种粒子处于可流动液体中，其它距离很远的相同粒子（即d≫λ）会移动到晶核处聚集，这是由于在其它位置粒子处于不稳定状态，而逐步位移过来的，本质上还是逐步移动的结果。见图2（a）。

b）当粒子间没有可流动性，使电磁力无法传递，粒子间又还原成粒子的空间相互作用状态，这时离子间就只有万有引力型弱相互作用。两个粒子间距离d≫r，并且没有可以传递的介质，两个粒子间φ1∩φ2≪1。φ1∩φ2→0，此时电磁力→0，粒子间仅存在万有引力弱相互作用，粒子不会聚集。见图2（b）。

（3）交集φ1∩φ2→0，所以D→0，lnP＝－2［2m（V0－E）］1／2D／ħ→0，则P→1表明没有相同的电磁辐射形成共振态，没有相同的波长电磁场相互作用，这种没有相同的波长电磁场作用，没有共振条件的约束，所以势垒是为零的，即不需要波长的一致性。共振势垒为零，有一最小的共振态，即万有引力。

表2估算了质子与质子，氢分子和甲基的D值及共振穿透几率因子P。核子取平均结合能8 MeV，核子的距离取最大10fm的一半5fm，得到的D值是1.1×1010nm－2，氢分子的D值是2.9× 10－2，甲基的D值是8.8×10－8。从式（16）可以估计核子的共振穿透因子P，三者P相差非常大，表明了核子是不容易被激发，需要极大的能量的单色光才能引起共振，甲基是最容易引起共振效应的。

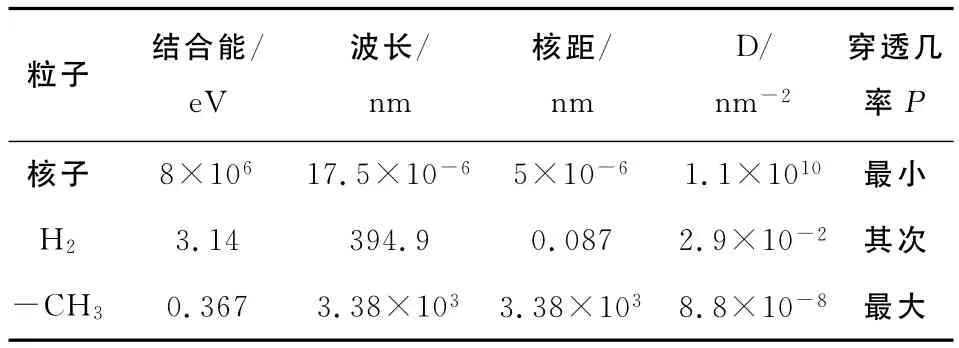
表2 几种粒子的D值及穿透几率PTable 2 Some particles Dvalue and penetration probability P

5 万有引力的量子化

5.1 零共振势垒

对于φ1∩φ2→0的弱共振场，可以认为是零共振势垒。对于零共振势垒，尽管两个粒子没有相互作用，其φ1∩φ2→0剩余最小趋于零的两个相反电磁场，也一定采取相反场相互吸引作用，来满足内敛性原理，这就产生了最小趋于零的电磁场相互作用，即万有引力作用，所以万有引力的本质仍然是电磁场相互作用，只不过是两个粒子的共振电磁场的交集趋于零，没有显示任何的电磁作用。

电磁波对称性电磁辐射共振交集φ1∩φ2→0，粒子间的共振势垒厚度因子D→0，则穿过势垒的几率lnP＝－2［2m（v0－E）］1／2D／ħ→0，所以P→ 1，表示穿过的几率为百分之百，完全穿过。这种最低值的共振效应，互相间不会产生阻隔作用，隧道效应具有最大值P→1，相应的共振势垒为零。

当r≫λ，l≫λ时，粒子的微小的扰动将会严重影响粒子1辐射的λ1与粒子2辐射的λ2的叠加，势垒降低φ1∩φ2→0，共振势垒厚度因子D→0，两粒子不能形成强共振态。如微米，毫米级粒子之间只能产生万有引力。宏观物体距离≫波长，具有无数的分子聚集，其共振交集φ1∩φ2→0，宏观粒子集合共振效应是一极限低值，相互作用力是万有引力。当两个粒子的距离d远远大于共振波长λ时共振辐射的交集φ1∩φ2→0，粒子间没有势垒D→0。由于这种共振场没有共振条件的限制，没能级跃迁限制，势垒为零，所以万有引力的共振场可以加和。

图5（a）是纳米氧化铝的TEM，从图中可以看出，粒子紧密的堆积在一起，由一次粒子堆积形成了二次纳米孔道，这个过程一次粒子是三价的铝原子与两价的氧原子中电子绕核产生的共振点，形成了内敛性的分子键，组成了氧铝基元，基元之间共振点的聚合，形成了一次粒子。一次粒子经聚集产生了二次粒子，这个二次粒子是有部分一次粒子有共振点共振，大部分是共振交集φ1∩φ2→0聚集，没有强的共振点作用。

图5（b）是由二次粒子堆积的约直径为100 nm，长为500nm左右的大颗粒，进一步自然堆积，形成了具有共振交集φ1∩φ2→0聚集体，这些聚集体的堆积成了适合大分子催化的氧化铝载体。

Fig.5 TYEM of nano－alumina and nanopore of weak interaction图5 纳米氧化铝粒子TEM和弱相互作用产生的纳米孔

万有引力就是这种具有共振交集φ1∩φ2→0的各种粒子的堆积体之间产生的相互作用，满足共振场的基本公式中与距离成反比的反比律规律。

5.2 零共振势垒的弱共振场内敛性作用原理

定义2： 对于φ1∩φ2→0两个相互作用粒子零共振势垒的共振场，将满足共振场的内敛性原理。

共振辐射交集为零的粒子的相互作用是弱共振场的相互作用，粒子间辐射产生的共振势垒为零，粒子间具有完全贯穿性的隧道共振效应。

零共振势垒的弱共振场所辐射的电磁场，还是存在电磁辐射的，这种辐射不会消失。由于φ1∩φ2→0，两者之间没有强的电磁相互作用，这种辐射还是要发生相互作用。在没有电力起作用的电磁场，这两个场一定是相反的场，否者将会发生电力作用，而电力作用是一个长距离有效的作用力，所以可以肯定两个粒子的φ1∩φ2→0产生的电磁场是具有正负电性相等的场。

根据共振场的内敛性原理，两个相反场的电磁场作用一定会采取吸引的方式发生作用。这样零共振势垒的弱共振场产生的两个相反场是一种最弱的相互作用场，即万有引力的重力场。

当粒子的粒度大于100nm以上，共振势垒将逐渐变为零势垒，到微米级以上，粒子间共振势垒就是零，之间相互作用就是万有引力，这是由于电子共振点半径就是原子共价半径或离子半径的平均值，超过这个半径，共振点辐射的电磁场就不会满足内敛性原理。

5.3 万有引力量子化

共振势垒为零，有一最小的共振态，即万有引力。势垒为零，这表示具有万有引力的宏观物体的相互作用是没有势垒的限制，势垒为零的物体间相互作用是任意质量的物体都具有的一种普遍的性质，即万有引力可以发生在微观物体到星体一切物体之间。

一切将万有引力量子化的实验都是徒劳的。这种势垒为零的共振态，之间传递的辐射是不能满足共振场的频率条件，其量子化也是为零的，万有引力不满足量子化条件，万有引力是非量子化的。

5.4 万有引力型弱共振场的加和性

零共振势垒的弱共振场加和性：具有共振势垒为零的共振场，由多粒子体系产生的共振辐射场具有加和性。

电子，质子都是费米子，两者之间互相作用产生的辐射是玻色子。根据基本粒子性质，可以得知，玻色子是具有加和性的。

对于φ1∩φ2→0的任意两个粒子费米子，m1，m2所产生的辐射场，由于两者之间没有共振频率，可以认为辐射的玻色子具有相同性质，即φ1，φ2辐射相同，都为Φ，可以进行加和

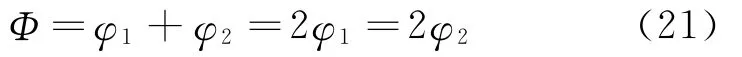
对于费米子粒子的聚合体m是m1，m2，m3，…，mi的之和，所产生的共振辐射Φ是φ1，φ2，…，φi之和。

6 弱共振场的等势线及万有引力公式的导出

1／（4πr2）是一个中心粒子能量向外辐射产生的等位面，这是共振场基本方程的能量传递的主要方式，表示能量以1／（4πr2）进行衰减。

在r处球面所具有的势能，是零势垒弱共振场的等位面。在球内以1／（4πr2）进行增加，在球外以1／（4πr2）进行衰减。

从质心的Δm1，每一微小的薄层Δmn与上一层的Δmn－1的Δφnn－1都→0。半径为r整个物体m共振辐射产生的弱相互作用力，具有加和性，设F0为地球地面的单位重力，m0为整个地球的质量，

令er＝Lrmr则，

当任意两个粒子的φ1∩φ2→0，令

则，

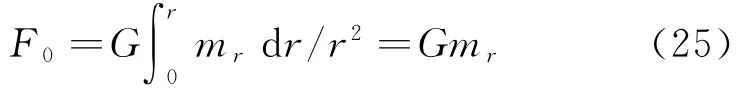
在球内的任意一点是随着半径增加重力是增加的。

在球外空间某一点r处的重力为，

式（26）与万有引力公式相同。

尽管，这里引用了万有引力常数G，具有对称性电磁波的φ1∩φ2→0，其共振场常数与经过试验验证的万有引力常数统一，是符合物理实在的。同时也赋予了万有引力常数新的意义，是对称性电磁波的弱共振场本身具有的属性，表示这种对称性电磁波的弱共振场，即使不能用电磁仪器测出，也表示这种弱共振场的质量提供了一最低极限值，这种势垒为零的共振场具有加和性，具有远程性。

7 光在弱共振场中的运动

光子是玻色子，无质量，具有质量的实物粒子都是费米子。任意两个大颗粒子都是由大量具有质量的费米子集合组成。两个大颗粒子相互作用仍能体现费米子性质。

费米子聚集体与玻色子聚集体之间的大差别，费米子聚集体是有质量，并且还是满足泡利不相容原理，这是由于大量费米子聚集体对外的辐射超过其共振点半径后，大颗粒的聚集体之间显示的就是φ1∩φ2→0性质，大颗粒之间满足共振场内敛性原理，这是符合能量守恒原理的。玻色子是无质量，并且不满足泡利不相容原理，在同一状态可以容纳无数的相同性质玻色子。当玻色子在由大颗粒费米子聚集体产生的弱共振型的引力场时，玻色子是不能与大颗粒费米子聚集体产生引力场发生相互作用，两者间没有内敛性原理束缚，不会发生吸引作用。

从以上分析来看，光子在地球和太阳这样具有质量的引力场中，是不会与太阳产生的引力场发生作用。所以光子在太阳的引力场中保持光线最小时间原理，做直线运动，而不是在太阳时空中做测地线运动，因为太阳的引力场对光子的作用无效。

8 结束语

（1）万有引力不满足量子化条件，万有引力是非量子化的；

（2）两个粒子共振有一共振能垒，一个粒子辐射的电磁场是否被另一个粒子吸收，辐射的频率与能吸收辐射的粒子产生的辐射频率必须满足共振条件，即频率相同或是整数倍；

（3）原子半径是原子中电子的共振点半径的平均值；

（4）共振势垒具有隧道效应，不能穿透的形成粒子共振状态，穿透的粒子没有共振相互作用；

（5）共振辐射的交集φ1∩φ2→1时，是粒子的强相互作用，当共振辐射的交集φ1∩φ2→0时，两个粒子产生最低的共振效应。万有引力是两个粒子的弱共振产生的相互作用力。当两个共振辐射的交集φ1∩φ2→0时，表示两个粒子没有共振频率；

（6）没有共振辐射的费米子粒子的集合体，仍然产生费米子性质，两个费米子集合体辐射出没有共振频率的辐射，但是在空间仍满足能量守恒原理，必须满足共振内敛性原理，两个费米子集合体产生一个最低的共振态－万有引力；

（7）光线在万有引力的弱共振场中保持直线性运动。

［1］ 刘辽，赵峥.广义相对论［M］.北京：高等教育出版社，2004：9－11.

［2］ 宁平治.李磊.闵德芬.原子核物理基础［M］.北京：高等教育出版社，2003：321－416.

［3］ 王正行.简明量子场论［M］.北京：北京大学出版社，2008：8－9.

［4］ Von Heisenberg W.Über den anschaulichen Inhanlt der quantentheoretischen Kinematik und Mechanik［J］.Phys.，1927，43，172－198.

［5］ Amati D，Ciafaloni M，Veneziano G.Superstring collisions an planckian energies［J］.Phys.B，1987，197：81－88.

［6］ Gross D J，Mende P F.String theory beyond the planck scale.Nucl［J］.Phys.B，1988，303：407.

［7］ Wi E.Reflections on the fate of spacetime［J］.Phys.today，1996，49：24－31.

［8］ Maggiore M.A generalized uncertainty principle in quantum gravity［J］.Phys.lett.B，1993，302：65－69.

［9］ Jizha P，Kleineert H，Scarsigli F.Uncertainty relation on a word crystal and its applications to micro black holes［J］.Phys.rev.D81，2010，81（8）：084030.

［10］ 王鼎聪.论振动体的电动力学（Ⅰ）—量子共振场［J］.石油化工高等学校学报，2012，25（1）：46－51.

［11］ 王鼎聪.论振动体的电动力学（Ⅱ）—共振场的波粒二像性运动［J］.石油化工高等学校学报，2012，25（2）：29－37.

［12］ Wang Dingcong.In situ synthesis of nanoparticles via supersolubilizing micelle self－assembly［J］.Sci.China ser.B－chem.，2007，50（1）：105－113.

［13］ 王鼎聪.纳米自组装合成大孔容介孔氧化铝［J］.中国科学B辑：化学，2009，39（5）：420－431.