3-TPT并联机构运动性能研究
杨 辉, 赵恒华, 付红栓
(辽宁石油化工大学机械工程学院,辽宁抚顺113001)
并联机床作为一种新概念机床[1-2],其具有许多传统机床所无法取代的优点。在对机构性能的分析中,机构的奇异性、运动灵巧性以及平稳性是评价并联机床运动性能和静力学性能的基础,也是衡量并联机床工作性能优劣的重要指标。本文基于一种3-TPT型并联机床作为研究对象,建立该机床的数学模型,求出雅可比矩阵及其逆矩阵,并在此基础上,运用MATLAB软件以及LabVIEW软件对该并联机构的奇异性、灵巧性和稳定性进行仿真分析,并将其作为以后最优化设计和控制系统设计的理论基础。
1 机构的组成
本文所依据的并联机构[3-5]主要由运动平台、固定平台、平行机构和驱动杆等几部分组成,其结构如图1所示。其中,平行机构由虎克铰、支撑杆和从动平台组成。固定平台与运动平台上的虎克铰均按正三角形分布排列,三根驱动杆并联安装;平行机构通过上、下虎克铰将固定平台和运动平台连接起来。机构中的3个移动副为3个驱动副,在伺服电机的驱动下,通过改变杆的长度,从而调整运动平台的位置。由于空间平行机构限制了该并联机构的3个转动自由度,所以运动平台只能在空间运动中保持平动。

Fig.1 The diagram of 3-TPT parallel mechanism图1 3-TPT并联机构简图
2 运动学方程的建立
建立如图2所示的空间坐标系[5]。机构上下平台的铰链中心点均按等边三角形布置,对应边分别平行,两平台相对位置在运动中总是保持平行,姿态上没有变化。首先,将基础坐标系Ob-XbYbZb建立在固定平台中心点上,其中Zb轴垂直向下,Yb过三角形顶点B1,Xb轴正向与边B1B3相交;然后,在运动平台的中心点上建立移动坐标系Op-XpYpZp,其中Zp垂直向下,Yp过三角形顶点A1,Xp轴正向与边A1A3相交。
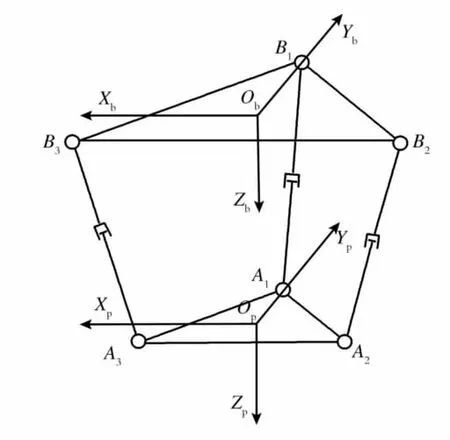
Fig.2 Space coordinate system of 3-TPT parallel mechanism图2 3-TPT并联机构的空间坐标系
令固定平台的外接圆半径为R,运动平台的外接圆半径为r,使得R>r;设三根驱动杆A1B1,A2B2,A3B3的长度分别为l1,l2,l3。由此可知固定平台3个顶点在基础坐标系Ob-XbYbZb中的坐标为:

同理,运动平台的3个顶点在移动坐标系Op-XpYpZp中的坐标为:

因为运动平台和固定平台保持平行,所以Op-XpYpZp相对Ob-XbYbZb的齐次变换矩阵为:
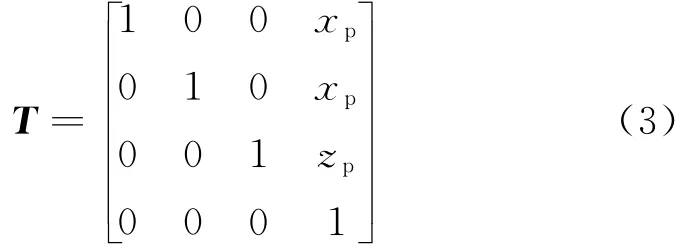
其中(xp,yp,zp)为移动坐标系的原点Op在基础坐标系Ob-XbYbZb中的坐标。
根据坐标变换理论,动平台3个顶点在基础坐标系Ob-XbYbZb中的位置可表示为:
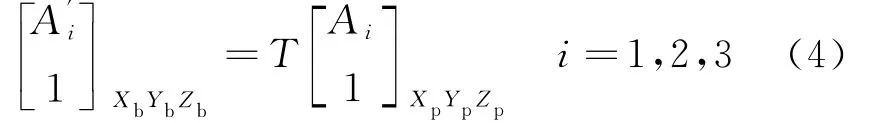

根据式(1)和式(5),由两点间距离公式可得:

其中c=R-r,xp,yp,zp为移动坐标系的原点Op在基坐标系Ob-XbYbZb中的坐标。该式称为机构位置反解表达式。
由式(6)可得出机构位置正解表达式为:
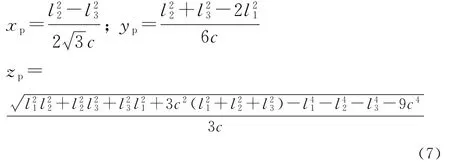
3 并联机构的奇异性研究
特殊位形是机构的固有性质,对于机构,特别是机器人机构的工作性能有着很大的影响。当机构处于某个特定形位时,其雅可比矩阵为奇异阵,且行列式为零,此时机构的速度反解不存在,这种机构的位形称为奇异位形。当机构处于该位形时,机构的操作平台将获得多余的不可控自由度或者变得刚化而失去部分自由度。当机构丧失某些自由度的同时也会失去一些功能,而如果机构增加了额外的自由度,将会使机构失控。所以机构在工作时要避开奇异位置。
在本文中用一阶影响系数作为评判3-TPT并联机构奇异性的标准。一阶影响系数是指从关节空间运动速度向操作空间运动速度传递的广义传动比,也即雅可比矩阵,其定义式为:

式中,w′为机器人末端在操作空间中的广义速度矢量,q′为关节速度矢量。按定义式,对式(7)两边求导,则可得到并联机构的雅可比矩阵为:
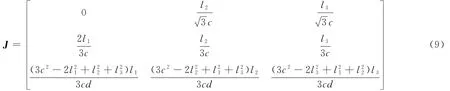
由MATLAB软件计算雅可比矩阵的行列式为:

由运动学正解方程(7)可知,zp≥0,所以移动平台只能处在固定平台的一侧,而不能翻转到另一侧。又因为实际机构中运动平台不能与固定平台重合,所以zp≠0。故而可知雅可比矩阵行列式|J|>0且不趋于∞,由此可知实际上该机构不存在不定位形。
4 并联机构灵巧性研究
机器人运动的灵巧性是指该系统在当前位形状态下沿指定方向运动的能力。它是机器人运动几何特性的一项重要指标,能够深刻地反应机器人的运动学性能。
为了使机器人在作业空间内任一位置的操作能力都能得到定量的评估,本文将利用雅可比矩阵的条件数K(J)作为评价机构灵巧性的衡量标准。通过矩阵的谱范数可知条件数与奇异值的关系为:

式中σmax和σmin是雅可比矩阵J的最大和最小奇异值。该指标称作各向同性指标,强调各方向的映射放大倍数不能差距太大。由式(11)可以看出矩阵条件数取值范围是:

当K(J)=1时,表示沿各个方向进行的映射放大倍数完全相等,这种位形称作各向同性。所以在设计机构时应使最小条件数在操作范围内尽量的小。
根据实验样机结构尺寸,取3-TPT并联机构各杆最小杆长Lmin=8 5 0mm,最大杆长Lmax=1 300mm,由此利用LabVIEW软件和MATLAB软件就可以仿真出K(J)在不同位形时的变化情况[7-8],仿真结果如图3,4所示。

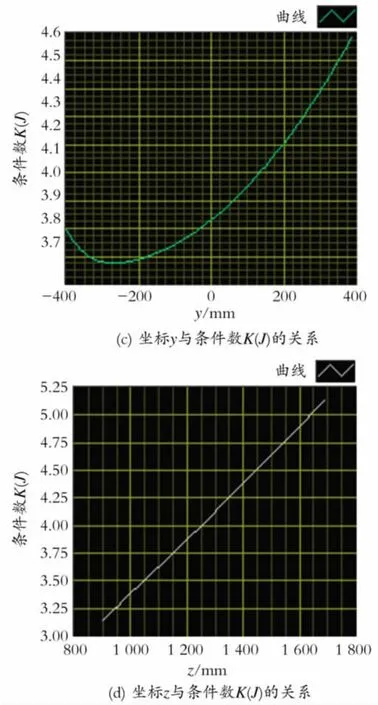
Fig.3 Dexterity analysis of parallel mechanism1图3 并联机构灵巧性分析1
由图3可以看出,条件数K(J)的变化与c的取值有着很大的关系,所以在满足机构合理的前提下,应使c的取值满足条件数最小的原则。由图3,4可知,条件数K(J)随机构位姿的变化而连续变化,没有突变发生,这表明机构没有奇异现象,并且在不同的运动状态下均存在最小K(J)值。这样在机器人结构设计时,可以根据仿真结果,避开K(J)值较大的范围,在满足工作要求的前提下,使K(J)的值尽可能的接近于1。

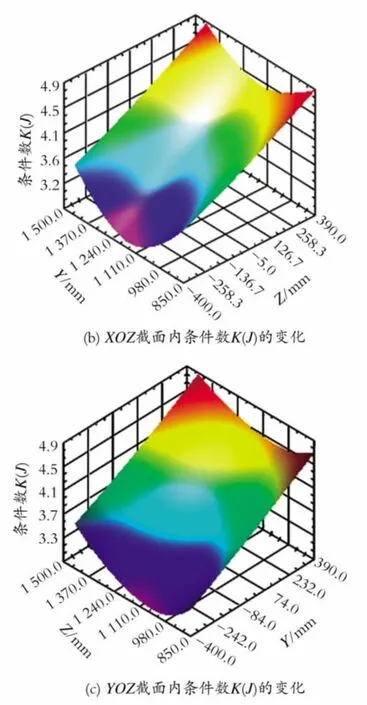
Fig.4 Dexterity analysis of parallel mechanism2图4 并联机构灵巧性分析2
Angeles和Rojas于1987年提出把最小条件数K(J)min的倒数定义为度量机构灵巧性的指标[6],其定义式为:
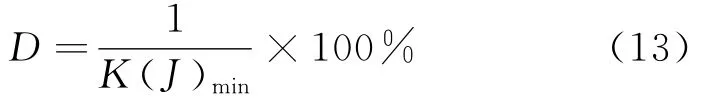
对于3-TPT并联机构而言,由参数搜索和仿真结果可知,其K(J)min=1.13,即该机构的灵巧性为88.5%,这表明3-TPT并联机构具有较好的灵巧性,且在其运动空间没有明显的奇异位姿。
5 并联机构平稳性研究
平稳性是衡量机构运动性能的重要指标之一。本文用3-TPT并联机构速度和加速度变化曲线的光滑程度作为平稳性的衡量标准。由(8)式可得,

式中q′为关节速度矢量,w′为机器人末端在操作空间中的广义速度矢量,雅可比逆矩阵为:

将公式(14)两边对时间求导,则可得到机构加速度表达式:
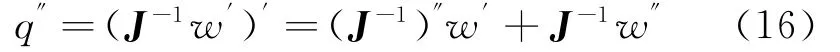
假设动坐标系原点Op在Z=1m的截面内,(xp,yp,zp)为移动坐标系的原点Op在基础坐标系Ob-XbYbZb中的坐标,其运动方程为xp=0.05cos(t),yp=0.05sin(t),运动时间t=10s。根据实验样机的结构尺寸,R=600mm,r=200mm。用MATLAB软件和LABVIEW软件得到的驱动杆l1,l2,l3伸缩速度及加速度变化曲线如图5所示。由图5可以看出,三根驱动杆的伸缩速度曲线和伸缩加速度曲线连续且非常光滑,故该机构具有较好的平稳性。

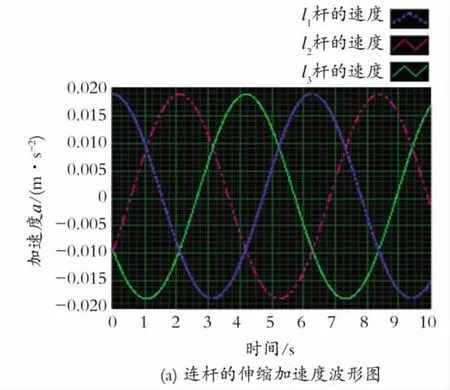
Fig.5 Stretching speed and stretching acceleration of the rods l1,l2,l3图5 l1,l2,l3三杆的伸缩速度和伸缩加速度
6 结束语
奇异性、灵巧性以及平稳性均是分析并联机构运动性能的重要指标。本文针对3-TPT并联机构,建立运动学方程、求解雅可比矩阵,利用MATLAB软件和LabVIEW软件对该机构的奇异性、灵巧性和平稳性做了仿真分析,结果发现该机构不存在奇异位形,并拥有较好的灵巧性和平稳性,为确定工作形位和机构尺寸提供了设计依据。
[1] 高天雷.国内并联机床的发展[J].航空制造技术,2010(4):60-62.
[2] ZHAO Jun—wei,DAI Jun,HUANG Jun-ji.3-PRS serial-parallel machine tool And enter identification[J].Journal of Chongqing university of posts and telecommunications(Natural science edition),2009,21(2):284-291.
[3] 王传强,赵恒华.3-TPT并联机床奇异性及平稳性研究[J].组合机床与自动化加工技术,2010,(10):26-28,36.
[4] 程仙国,赵恒华.基于Matlab对3-TPT并联机床的运动学仿真[J].辽宁石油化工大学学报,2008,28(1):19-22.
[5] 孙希龙,蔡光起.三杆并联机器人计算机仿真研究[D].沈阳:东北大学,1999.
[6] 吕春梅,谢里阳.3-TPT型并联机床仿真分析与研究[D].沈阳:东北大学,2005.
[7] 崔智全,赖一楠,赵韩涛,等.MATLAB 2009从入门到精通[M].北京:中国铁道出版社,2011.
[8] 曲丽荣,胡容,范寿康.LabVIEW、MATLAB及其混合编程技术[M].北京:机械工业出版社,2011.

