可加函数方程在广义函数空间上的稳定性

朴青松，金英山，李林松＊

（1.延边大学理学院 数学系，吉林 延吉133002；2.延边一中，吉林 延吉133000）

可加函数方程在广义函数空间上的稳定性

朴青松1，金英山2，李林松1＊

（1.延边大学理学院 数学系，吉林 延吉133002；2.延边一中，吉林 延吉133000）

利用广义函数正则化的方法给出1个可加函数在广义函数空间上的一般解，并且利用热方程的核给出该函数方程在缓增广义函数上的Hyers－Ulam－Rassias型稳定性，进一步推广了文献［1］的结论.

广义函数；热方程的核；可加函数方程；稳定性

0 引言

2007年，P.Nakmahachalasint［1］给出了1个n个变量的可加函数在赋范空间上的函数方程的稳定性定理：

定理1 设X是向量空间，Y为Banach空间.如果映射f∶X→Y对所有x1，x2，…，xn∈X满足，则存在1个唯一的线性映射L∶X→Y，使得L满足函数方程，并且对所有x∈X，有

本文主要研究含有3个变量的可加函数，即

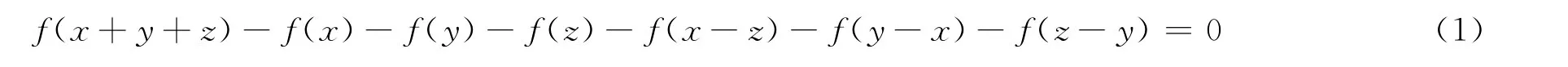
在缓增广义函数空间S′（Rn）上的一般解及其Hyers－Ulam－Rassias函数方程的稳定性.类似于文献［2－4］中的方法，首先将方程（1）及其不等式在广义函数空间上重新定义.即设A，B1，B2，B3，P1，P2，P3分别为：A（x，y，z）＝x＋y＋z，B1（x，y，z）＝x－z，B2（x，y，z）＝y－x，B3（x，y，z）＝z－y，P1（x，y，z）＝x，P2（x，y，z）＝y，P3（x，y，z）＝z，x，y，z∈Rn，则式（1）和相应的不等式可重新描述为

对于广义函数的拉回（pullback）u◦A，u◦B1，u◦P1有下列运算［5］：

1 基本概念

定义1［5－6］若Rn上的无穷可微函数φ，∀α，β∈Nn0，满足不等式，则称φ为速降函数.速降函数全体构成的线性空间记为S（Rn）或者S，由拟范数族φα，β使S成为Frechet空间.设u是S（Rn）上的线性泛函，若存在C＞0及非负整数N，使得对任意φ∈S（Rn），有则称u为缓增广义函数.缓增广义函数全体记为S′（Rn）.

称其为广义函数u的高斯变换.

引理1［7］设u∈S′（Rn），则其高斯变换~u（x，t）是热方程的无穷可微解且满足：①存在正数C，M，N，使得当t→0＋时，~u（x，t）→u（S′），即对于任意φ∈

2 S′（R n）上可加方程的一般解及其稳定性

下面给出方程（2）在广义空间S′（Rn）上的一般解及不等式（3）的 Hyers－Ulam－Rassias稳定性定理.用热方程的核的张量积Et（ξ）Es（η）Er（ζ）对方程（2）做卷积，由（4）式可得

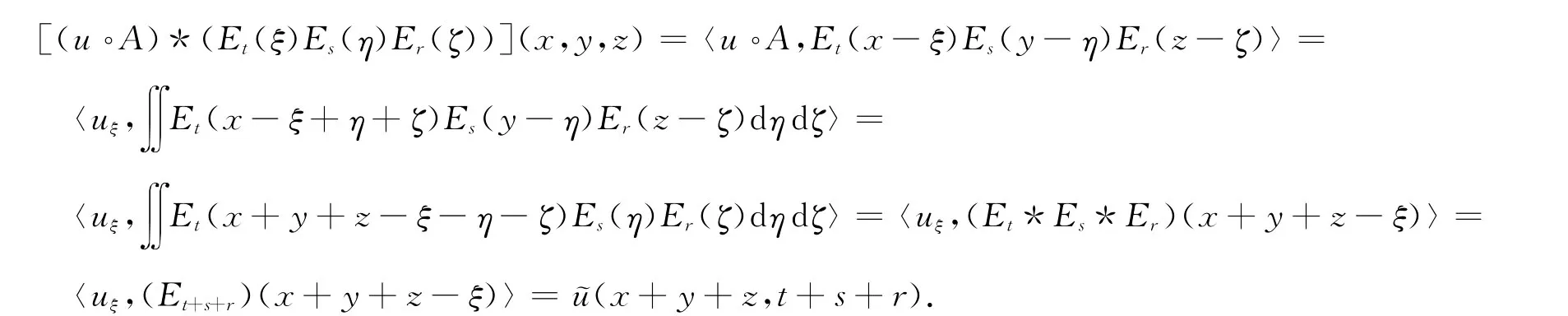
类似的有：

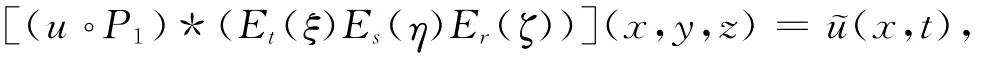
引理2 若函数f∶Rn×（0，＋∞）→C连续，且对所有x，y，z∈Rn，t，s，r＞0满足

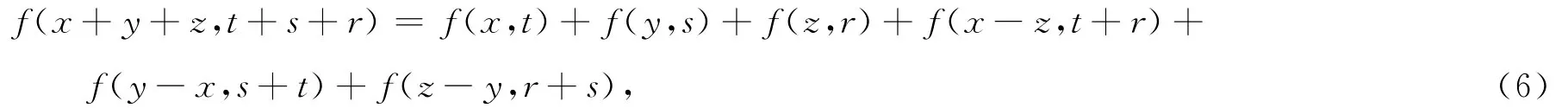
则存在bi∈C，使得其中x＝ （x1，x2，…，xn）∈ Rn，t＞0.

证明 由（6）式易知，对每个x∈Rn，f（x，0＋）∶＝limt→0＋f（x，t）存在.令x＝y＝z＝0，t＝s＝r→0＋，则由（6）式可得f（0，0＋）＝0.在（6）式中，令x＝y＝z＝0，则有f（0，t＋s＋r）＝f（0，t）＋f（0，s）＋f（0，r）＋f（0，t＋r）＋f（0，s＋t）＋f（0，r＋s）.令t＝s，r→0＋，由f（0，0＋）＝0，可得对所有的t＞0，f（0，t）＝0.在（6）式中，设y＝z＝0，则由f（0，t）＝0可得

令s→0＋，即可得到f（x，t）＋f（－x，t）＝0.再由式（7）有f（x，t＋s＋r）＝f（x，t）＋f（x，t＋r）－f（x，s＋t）.令r→0＋，可得f（x，t＋s）＝f（x，t）.这个等式说明函数f（x，t）与t无关.因此，设h（x）＝f（x，t），由式（6）有h（x＋y＋z）＝h（x）＋h（y）＋h（z）＋h（x－z）＋h（y－x）＋h（z－y）.根据文献［1］的定理2.1和h的连续性，f（x，t）可以表示为，其中bi∈C.证毕.

由引理2可得到下面的结论.

定理2 设u∈S′（Rn）满足方程

证明 用Et（ξ）Es（η）Er（ζ）对方程（8）的两边做卷积可得，其中~u是u的高斯变换.因为~u是无穷可微函数，故由引理2可得其中bi∈C.令t→0＋，由引理1中的条件②即得证毕.

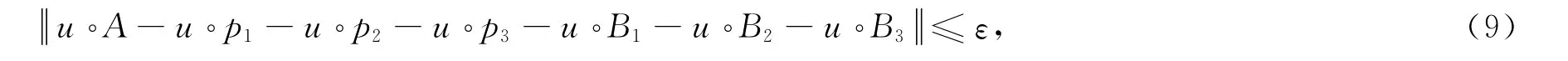
下面给出本文的主要结论.

定理3 若u∈S′（Rn）满足不等式其中bi∈C，xi∈R.

证明 类似于前面的方法，对不等式（9）的两边用Et（ξ）Es（η）Er（ζ）做卷积，可得

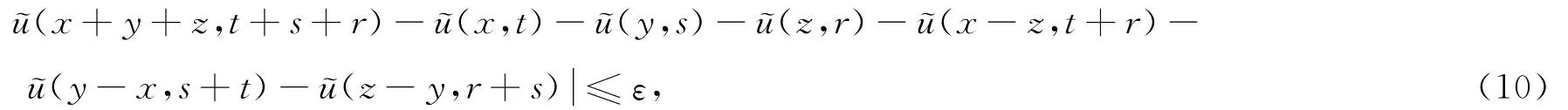
其中x，y，z∈Rn，t，s，r＞0，~u是u 的高斯变换.设，则h（0，t）＝0，并且

由（13）式容易证明，对每个（x，t）∈Rn×（0，＋∞），｛2－kh（2kx，t）｝∞k＝1是局部一致柯西序列，因此，由式（11）和（13）知，g（x，t）∶＝limk→∞2－kh（2k，t）是Rn×（0，＋∞）上的连续函数并且满足g（x＋y＋z，t＋s＋r）＝g（x，t）＋g（y，s）＋g（z，r）＋g（x－z，t＋r）＋g（y－x，s＋t）＋g（z－y，r＋s），且以此类推，可得

由（10）式知，c∶＝lim supt→0＋f（0，t）存在.在（10）式中，设x＝y＝z＝0，t＝s，并令r→0＋，可得.因此，

在（16）式中，设tn→0，使得当n→∞时，f（0，tn）→c，则.故由（16）式知，

证毕.

注1 由不等式（17），u－L（x）属于（L1）′＝L∞，因此u∈S′（Rn）可唯一地表示为u＝L（x）＋υ，其中υ是有界可测函数，并且因此，在（15）式中，令t→0＋，即得

注2 对于n个变量的可加函数可以用完全类似的方法获得相类似的结果.

［1］Nakmahachalasint P.On the Hyers－Ulam－Rassias stability of ann－dimensional additive functional equation［J］.Thai Journal of Mathematics，2007，special issue：81－86.

［2］Lee Y S.Stability of a quadratic functional equation in the spaces of generalized functions［J］.Journal of Inequalities and Applications，2008：210615.

［3］Chung J.Stability of functional equations in the space of distributions and hyperfunctions［J］.J Math Anal Appl，2003，286：177－186.

［4］Chung J.A distributional version of functional equations and their stabilities［J］.Nonlinear Analysis，2005，62：1037－1051.

［5］Hörmander L.The Analysis of Linear Partial Differential Operator I［M］.Berlin：Springer－Verlag，1983.

［6］Schwartz L.Théorie Des Distributions［M］.Paris：Hermann，1966.

［7］Matsuzawa T.A calculus approach to hyperfunctionsⅢ［J］.Nagoya Math J，1990，118：133－153.

Stability of an additive functional equation in the space of generalized functions

PIAO Qing－song1，JIN Ying－shan2，LI Lin－song1＊
（1.DepartmentofMathematics，CollegeofScience，YanbianUniversity，Yanji133002，China；2.YanbianNo.1HighSchool，Yanji133000，China）

We investigate the general solution of an additive functional equation in the space of generalized functions using the method of regularizing distributions，and give the Hyers－Ulam－Rassias stability of an additive functional equation in the space of tempered distributions using heat kernel.Our results generalize the reference of［1］.

distributions；heat kernel；additive functional equation；stability

O178；O177.4

A

1004－4353（2012）01－0013－04

2012－01－09

教育部留学归国人员科研启动基金资助项目（教外司留［2008］890号）

＊通信作者：李林松（1968—），男，博士，副教授，研究方向为应用泛函分析.