关于丢番图方程x2+y3=z4的讨论

管训贵

（泰州师范高等专科学校 数理信息学院，江苏 泰州 225300）

关于丢番图方程x2+y3=z4的讨论

管训贵

（泰州师范高等专科学校 数理信息学院，江苏 泰州 225300）

利用解序列的递归性，得到了丢番图方程x2+y3=z4的一族非负整数解．

丢番图方程；解序列的递归性；非负整数解

1 引言及主要结论

1952年，L.E.Dickson在文献[1]中介绍Mathieu证明了丢番图方程

有无穷多组非负整数解，但并没有给出这些解的计算公式．1960年，E. Kiss在限制条件

的情况下讨论了方程(1)[2]．

本文运用 Pell方程 x2- 2 y2=±1的解序列的递归性质，给出丢番图方程(1)的一族非负整数解，即下面的定理1．

式中n为正整数．

2 关键性引理

引理1 若(xn,yn)是Pell方程 x2-2y2=1的任一非负整数解，则该方程的全部非负整数解可以由下式给出：

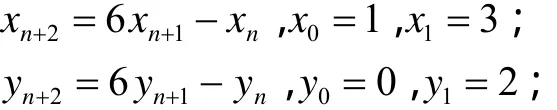
其中n为非负整数．

证明：根据文献[3―6]的结论可知，Pell方程x2- 2 y2= 1 的全部非负整数解为

引理1证毕．

仿引理1的证明可得引理2．

引理2 若(xn，yn)是Pell方程 x2-2y2=-1的任一正整数解，则该方程的全部正整数解可以由下式给出：

其中n为正整数．

3 定理的证明

设(xn， yn，zn) 是方程(1)的一组非负整数解，则方程(1)可化为

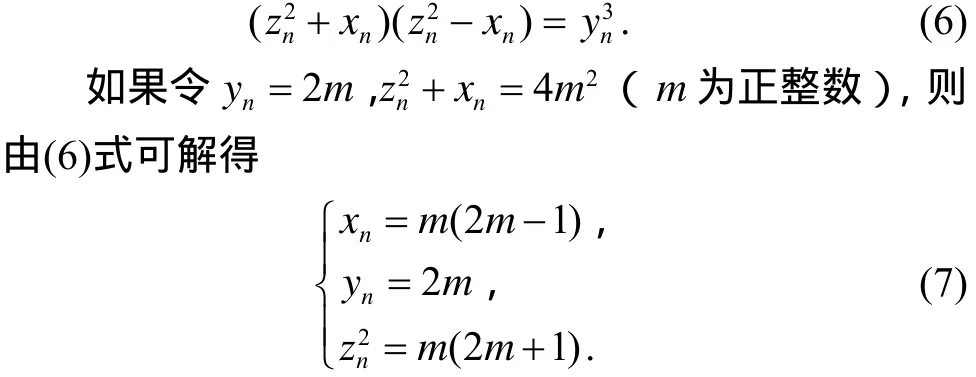
因为gcd(m ，2 m +1)=1，则由(7)式的第三式得

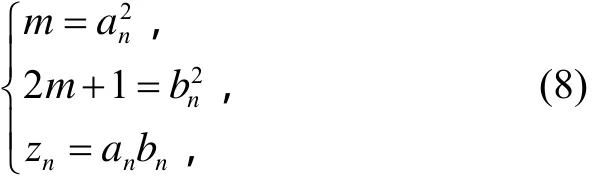
这里 an， bn是互素的正整数．因此，

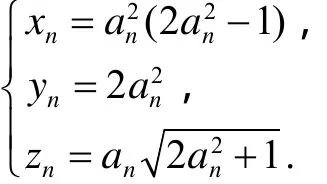
另由(8)式的前两式可得 bn2-2an2=1，根据引理1，an适合(2)式．

如果令 yn=2m - 1 ， zn2+xn= ( 2 m -1)2（m为正整

数），则可由(6)式解得

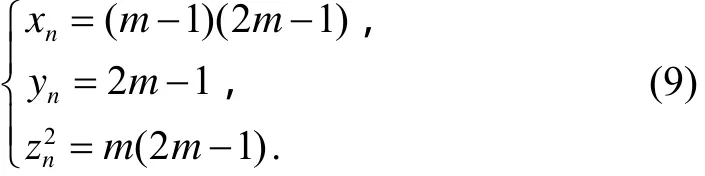
因为gcd(m ， 2 m -1)=1，故由(9)式的第三式得

这里 an， bn是互素的正整数．因此，

另由(10)式的前两式可得 bn2-2an2=- 1 .根据引理 2，an适合(3)式．

定理1证毕．

[1] Dickson L E．History of the Theory of Numbers[M]．Volume Ⅱ．Chelsea，1952．

[2] Kiss E．Rezolvarea in number naturale a eautiei diofantine x2+y3=z4[J]．Studia Univ. Babes-Bolyai. Ser Ⅰ Math. Phys.，1960(1)：15―19．

[3] 华罗庚．数论导引[M]．北京：科学出版社，1979：286―289．

[4] 曹珍富．丢番图方程引论[M]．哈尔滨：哈尔滨工业大学出版社，1989．

[5] 柯召，孙琦．谈谈不定方程[M]．上海：上海教育出版社，1980：17―28．

[6] 管训贵．初等数论[M]．合肥：中国科学技术大学出版社，2011．

Discuss on the Diophantine Equation x2+y3=z4

GUAN Xun-gui

(Taizhou Normal College, Taizhou Jiangsu 225300, China)

The non-negative integer solutions which satisfy the conditions to the Diophantine equation x2+y3=z4is proposed in by using the recursive property of solution sequence.

Diophantine equation; recursive property of solution sequence; non-negative integer solution

O156

A

1006-5261(2012)02-0003-02

2011-12-05

泰州师范高等专科学校重点课题资助项目（2010—ASL—09）

管训贵（1963―），男，江苏兴化人，副教授．

〔责任编辑 张继金〕