圆形分布资料配对样本角分析*
程 琮 刘一志
(泰山医学院卫生统计学教研室, 山东 泰安 271016)
1 参数配对样本角检验
对两样本圆形配对数据的检验称为参数配对样本角检验(parametric paired-sample testing with angles)。由配对角之间的差值形成单样本数据。配对角的差值计算如下:
Xj=cosα2j-cosα1j(1)
Yj=sinα2j-sinα1j(2)
二级数据(second-order data):如果一个样本数据对的每个数据是一个均角,并具有相应的向量长度r值,那么,就能进行二级分析。如果下面的公式分别取代公式(1)和(2),则可以使用Hotelling检验。
例1 研究人员研究10个鸟早上和下午坐落在树上的位置。每个鸟为一个样本,计算出坐落树的位置均角。试进行圆形分布配对样本的Hotelling检验。
(1)建立检验假设
H0:鸟所坐落的树位置在早上和下午相同。
H1:鸟所坐落的树位置在早上和下午不同。
取α=0.05。
(2)计算检验统计量(表1)

表1 角数据配对样本的Hotelling检验
k=10
应用公式有:
=216.8938
(3)确定P值,推断结论
根据自由度υ1=2,υ2=8,查单侧F界值表,得界值F0.05(1),2,8=4.46。本例,F=216.8938,大于界值F0.05(1),2,8=4.46,则P<0.05,在α=0.05水准上,拒绝H0,接受H1。
结论:10只鸟所坐落树的位置在早上和下午不同。
2 非参数配对样本角检验
配对样本圆形数据可以应用配对差值法形成一个单样本,并用非参数方法进行检验。该检验方法称为Moore检验。为每对差值计算直角坐标(Xj和Yj)值,对于j对差值的每一个,则有:
对rj值编排秩次,秩次i从1到n,用n代替k。并且应用下列公式进行分析。
二级数据:如果每对圆形数据是一个均角αj,具有向量长度rj,则此数据为圆形分布的二级数据。例2仍然用例1为例题。试进行圆形分布配对数据的Moore检验。
(1)建立检验假设
H0:鸟所坐落在树上的位置在早上和下午相同。
H1:鸟所坐落在树上的位置在早上和下午不同。
取α=0.05。
(2)计算检验统计量(表2)

表2 圆形分布配对数据的Moore检验
n=10
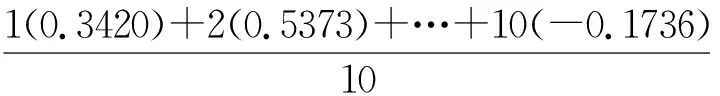
=-0.0706
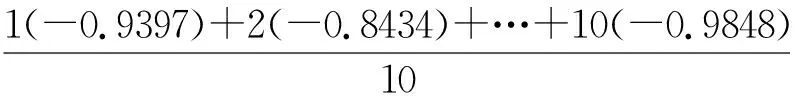
=-5.1857
(3)确定P值,推断结论
根据n=10,α=0.05,查表3 圆形分布Moore 检验界值表,得界值R'0.05,10=1.048。

表3 圆形分布Moore检验R'界值表
本例:计算的R'=1.6414,大于R'0.05,10=1.048,则P<0.05。在α=0.05水准上,拒绝H0,接受H1。
结论:鸟所坐落在树上的位置在早上和下午不同。
[1] Zar JH. Biostatistical analysis[M]. NJ:Prentice-Hall Inc,1999:645-649.
[2] Hotelling H. The generalization of Student’s ratio[J]. Ann Math Statist, 1931,2:360-378.
[3] Moore BR. A modification of the Rayleigh test for vector data[J]. Biometrica, 1980, 67:175-180.

