改进的邻域均值滤波去噪算法研究
牛秀琴
(四川师范大学 数学与软件科学学院,四川 成都 610066)
改进的邻域均值滤波去噪算法研究
牛秀琴
(四川师范大学 数学与软件科学学院,四川 成都 610066)
邻域均值滤波算法作为图像去噪算法的经典方法,不仅可以有效地消除噪声对图像的干扰程度,并且能够快速平滑图像,但它的缺点是会使图像边缘模糊,窗口越大,模糊程度越明显。本文针对椒盐噪声,分析原邻域均值滤波算法,通过与能量最小化原理相结合,提出新的改进的邻域均值滤波算法,这个算法构造了两个不同能量最小化函数模型,即E1模型和E2模型。两个模型均从图像像素点局部邻域出发,通过求解局部邻域能量最小判断是否利用邻域均值替换原像素灰度值。这个新的去噪算法不仅改变了原邻域均值滤波算法单一的替换灰度值的做法,降低了将非噪声点误判为噪声点的可能性,并且可以根据图像的大小自适应调节阈值,最后达到去除噪声的效果。通过与邻域均值滤波算法进行实验对比,取得较好的去除噪声效果。
图像去噪;邻域均值滤波算法;能量最小化
引言
图像去噪作为图像处理的一个重要环节,不仅可以帮助人们更加准确的运用图像,并能应用到其他众多领域,例如医学、物理、航天等。图像去噪算法可以有效地降低噪声对原始图像的干扰程度,并且增强视觉效果。图像去噪算法的经典算法很多,如文献[1]-[5]。这些方法被应用到很多领域,并且产生了很多的改进方法。
本文基于邻域均值滤波算法,基于能量最小化原理,对其在最小化局部邻域能量的过程中判断噪声点来替换灰度值并加以恰当的自适应阈值作为判断条件,不仅增强图像去除噪声的效果,并且能够很好的保持图像边缘信息。本文将在第一章介绍邻域均值滤波原理;第二章介绍能量最小化原理;第三章主要介绍改进的邻域均值滤波去噪算法;第四章给出相关的实验结果分析比较;最后在第五章给出结论。
1 邻域均值滤波
首先我们先来看图像中邻域系统[6]的概念:邻域系统:
图像中像素点p(i,j)通过周围的像素点集合U与另一个像素点 q(i,j)相关。p(i,j)的邻域系统 Np°定义为:
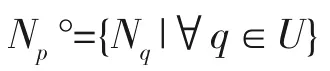
从上面定义可以看出像素点p(i,j)的邻域系统Np°是不包含其自身的,我们也可以称之为空心邻域系统;若加上像素点 p(i,j)本身,则表示为 Np或者 N。
通常情况下,对于一幅给定的图像G,若它的每个像素点为 p(i,j),我们取其邻域 N。邻域 N 的形状和大小可以根据图像特点确定。一般情况下,取的邻域形状为正方形,矩形或是十字形。现在常用邻域系统[7][8]有4-邻域系统,8-邻域系统,12-邻域系统,如下图表示。图1.1中以实心点为中心,小点的虚线方框包含的邻域范围称作4-邻域,即图1.2;图1.1中以实心点为中心,实线方框包含的邻域范围称作8-邻域,即图1.3。图1.1中以实心点为中心,大些的虚线方框包含的邻域范围称作12-邻域,即图1.4。

图1.1
图1.2
图1.3
邻域均值滤波是一种线性滤波法,它主要是为了去除图像扫描过程中产生的颗粒噪声,主要采用的是邻域平均法[8][9]。邻域平均法是用像素点 p(i,j)和其邻域N中全部点的像素灰度均值替换像素点p(i,j)对应的灰度值f(i,j)。4-邻域系统、8-邻域系统以及12-邻域系统的均值滤波算法数学表达式分别是(1.1)和(1.2)是在图像上3×3的正方形滑动窗口下内计算均值的;而(1.3)是在图像上5×5的正方形滑动窗口下内计算均值的。


下面我们举个实例:我们选取图像lena.png(大小为512*512)作为对象,采用8-邻域系统(即式子(1.1.2))对其进行邻域均值滤波处理,取对应矩阵的一部分进行比较,其中 x=2,3,4,5,6,y=8,9,10,如下图1.5:
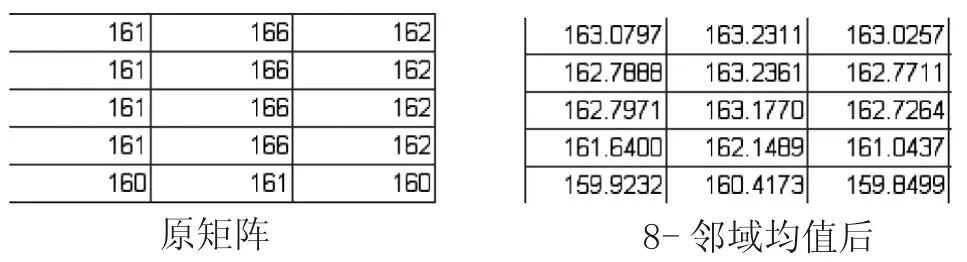
图1.5
通过观察图1.5,我们发现矩阵中每一个像素灰度值都是用周围8个像素灰度均值替换,比如:
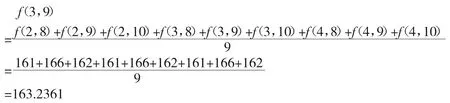
邻域均值滤波算法对于去除包含低密度噪声图像噪声是一种比较有效的去除噪声方法。它利用灰度均值替换,减小图像噪声方差,达到去除噪声的目的。
下面我们对图像couple.bmp(大小为256×256)通过8-邻域系统邻域均值滤波作用,给出对比图像,如下图1.6:

图1.6
从上图1.6,我们可以发现邻域均值滤波处理后的图像变得比原始图像模糊,这也是它存在的一个缺点:模糊图像细节。特别的,随着邻域系统的增大,图像模糊的程度越明显。
2 能量最小化原理
能量最小化[10]最初是源自图论相关的最大流最小割定理[11][12]。下面我们先来介绍这个定理:
最大流最小割定理[11][12]在任何网络中,最大流的值等于最小割的容量,即fmax=cmin(K)。
上面的最大流与最小割定理,为图像处理提供了方便。这样在我们求解最大流问题时就可以转化成求解最小割问题。图论中,最小割即网格内点的连线上的容量。我们将图像数字化后的矩阵看成网格,那么矩阵的元素即网格的每个顶点,通过构造一定的能量函数来计算每个顶点之间容量,即将最小割问题应用到图像处理内就表现为最小化能量函数值。下面我们用图像知识来详细解释这个问题。
在图像处理中,通常情况下我们将图像数字化后可看成是有很多像素点p(i,j)∈p构成的一个矩阵T,这个矩阵的每一个元素就是像素点所对应的灰度值fp(i,j)∈F。当我们给原本的图像加入噪声后,就会发现原图对应的像素灰度值发生改变,那么去除图像噪声就转化成纠正噪声点的灰度值问题。椒盐噪声是将图像中原本像素点变成黑点或白点,对应的像素值也就是由原来的0-255变成0或255。那么对于图像来说,如何才能够将像素点p(i,j)∈p与它的邻居用能量联系起来并达到最小化呢?在实际运算中,能量函数的计算就是通过我们前面提到的邻域系统将像素点联系起来。能量函数的构造方法如下:
一般的,图像上像素点 p(i,j)∈p 的能量函数用E(f)表示,在图像去噪中E(f)由两部分构成:
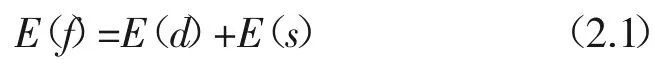
式子(2.1)中 E(d)表示势能团的能量值,E(s)表示像素点灰度替换值与像素点灰度原值的能量值。
对于图像去噪,最重要的就是如何构造E(f)中的E(d)与E(s)。本文改进的邻域均值滤波算法的能量函数具体构造方法将在下一章具体说明。
3 改进的邻域均值滤波算法
基于原本的邻域均值算法,并结合能量最小化[10]的原理在是否替换像素点值加了自适应阈值作为判断条件,更准确地进行噪声点灰度值的更换,具体步骤如下:
1)对原本大小为c×d的图像A加一定噪声系数的椒盐噪声得到图像B;
2)令图像C等于图像B,通过下列数学表达式(3.1)计算图像C的每一个像素点对应的能量初始值E0,并且计算所有像素点的E0之和E00。按照所定义的能量函数表达式不同,将其称为模型E1和模型E2,如下:
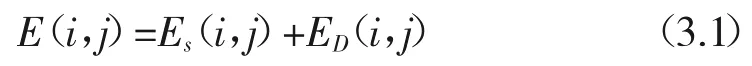
其中Es、ED有两种定义的方式:

上面的数学表达式(3.1)所计算的能量函数值能表现邻域系统(本文两种算法模型采用4-邻域系统,可根据实际需要改动)内图像每个像素点与周围像素点的一个差异程度,从能量的角度可以称上式的E为像素点的能量函数。
其中,Es表示像素点 p(i,j)自身的能量势能,ft(i,j)表示p(i,j)替换后的像素灰度值,f(i,j)表示p(i,j)的数字化图像后显示的灰度值;E(d)表示势能团内像素点p(i,j)与其他各点的能量值。
3)利用邻域均值算法替换每个像素点的灰度值,本文将采用8-邻域系统和12-邻域系统。
4)计算此时每个像素点相对应的E,计算方法同步骤2)。
5)依次通过比较每个像素点E与E0的大小关系并设定一定的阈值,判断是否需要用均值替换原像素值。具体规则:如果满足条件E<E0且E00/w<E0,其中 w 为约束阈值,w=(c-1)×(d-1),c,d 为步骤1中图像的大小,则用邻域均值替换原本的像素点值;否则,不替换,仍保持原本像素值。完成之后,保存图像为C1。(为得到更好的去除噪声效果,此步骤可以迭代多次)
6)完成上面替换,保存图片,计算原始图像A与C1的最小均方根误差MSE值(Mean Square Error)与峰值信噪比PSNR值(Peak Signal to Noise Ratio)。
PSNR是一种应用最广泛,最普遍的评价图像质量的客观标准,它的单位是dB。它具有一定的局限性,在许多实验结果都显示,PSNR的数值无法和人眼看到的视觉品质完全一致,可能会出现一下情况:第一、PSNR值较高,但视觉上看起来效果不好;第二、PSNR较低,但视觉上图像质量更清晰。
MSE是一种经过多次实验验证的较好的评判图像质量的客观标准。
本文采用的计算MSE值与峰值信噪比PSNR值的方法分别如下式:
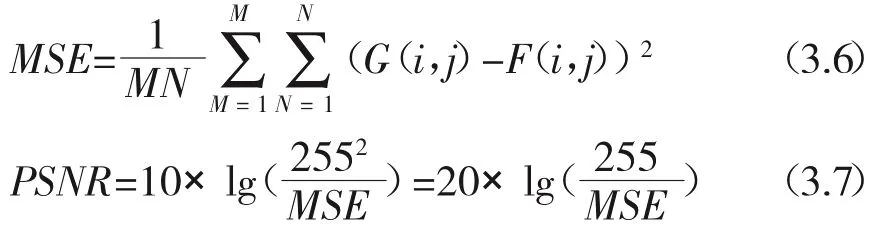
上式中:M,N表示图像数字化后的矩阵横坐标与纵坐标的值,即图像的大小为M×N是对应的,G(i,j)表示不含噪声的原图像的像素灰度值,F(i,j)表示去除噪声后的图像的像素灰度值。
判断标准:PSNR值越高,MSE值越低,图像去除噪声效果越好。
4 相关实验结果比较
我们选取8-邻域与12-邻域系统作为上小节算法步骤3)中提到的可选的邻域系统,分别在两种邻域下对图像进行去除噪声实验,比较改进均值滤波算法与原均值滤波算法结果。实验采用图像大小为256*256的diamond.png作为测试图像,噪声系数为0.08的椒盐噪声。经过实验研究,当模型E1和模型E2迭代次数为38次,基本可达到最优去除噪声效果。下图4.1与图4.2分别表示选择邻域系统为8-邻域系统与12-邻域系统的实验结果;同时用表格的形式将对应图像的MSE值与PSNR值给出,如表4.1,表4.2:

表4.1 图4.1对应的PSNR值与MSE值

表4.2 图4.2对应的PSNR值与MSE值
从视觉上看图4.1,可以明显看到在8-邻域系统下,模型E1和模型E2的去除噪声效果比原邻域均值滤波算法好得多。从表4.1可得,模型E1的PSNR值最高,MSE值最小,去除噪声效果最好。

图4.1

图4.2
从视觉看图4.2,可以明显看到在12-邻域系统下,模型E1和模型E2的去除噪声效果比原邻域均值滤波算法好得多。从表4.2可得,模型E1的PSNR值最高,MSE值最小,去除噪声效果最好。但是两图说明:12-邻域系统的效果没有8-邻域效果好,这是因为此法是基于邻域均值滤波算法,继承了它的缺点:邻域越大,滑动窗口随之增大,模糊图像的程度增强。
通过试验比较,我们发现此方法可以有效的替换噪声点的像素灰度值,并且可以取得很好的效果。
我们还对其他测试图像进行了测试,下面仅将图像pallon.pgm(图像大小为256*256)结果给出,噪声系数同样为0.08,邻域系统选择8-邻域,如图4.3:

表4.3 上图4.3的PSNR值与MSE值

图4.3
从上面看出,对于图像pallon.pgm的去除噪声的视觉效果模型E1和模型E2差不多,但从表4.3得PSNR值与MSE值上可得到模型E1比模型E2稍好些。
5 结论
改进邻域均值滤波算法通过对传统的邻域均值滤波算法进行分析,基于能量最小化原理,通过构造新的能量函数,提出了是否替换像素灰度值的判断方法,在去除噪声的同时更有效地保证了图像的边缘和纹理信息。通过实验比较,可以发现E1模型有较好的实验效果;选取8-邻域系统比选取12-邻域系统去除噪声效果更好,并有较高的PSNR值。此方法的优点是可以应用到其他经典方法之上以及更大的窗口系统,并且可以根据图像的大小自动调节约束阈值。同时计算量也没有增加很大的负担,时间上与原来邻域均值滤波去噪算法差别不大。
总之,改进的邻域均值滤波算法不仅可以增强去噪效果,同时可以很好的保持边缘与细节,并且可以应用到其他经典方法之上或其它领域,比如低质文字提取骨架以及去除含有噪声文字的噪声问题[6][7][8]以及图像分割问题[13]等领域。。
[1]王民,文义玲,常用图像去噪算法的比较与研究[J].西安建筑科技大学学报(自然科学版).2010,25(6):895-898.
[2]方莉,张萍.经典图像去噪算法研究综述[J].工业控制计算机,2010,(11):73-74.
[3]王秀芳.数字图像的噪声及其去噪的几种方法研究[J].黑龙江科技信息,2010,(31):53-55.
[4]仲崇丽.数字图像去噪方法的比较与研究[J].中国新科技新产品,2010,(15):41-41.
[5]陆雨花,章勇.图像去噪技术探讨[J].科技经济市场,2007,(10):164-165.
[6]侯显玲,低质汉字骨架提取研究[D].四川师范大学研究生论文,2011.
[7]陆天华.数字图像处理[M].北京:清华大学出版社,2007.
[8]张德丰.数字图像处理(MATLAB 版)[M].北京:人民邮电出版社,2009.236-237.
[9]四维科技,胡小锋,赵辉.图像处理与识别实用案例精选[M].人民邮电出版社,2004.
[10]Boykov Y.Veksler O.Zabih R.Siemens Corp.Res.,“Princeton,NJ.Fast approximate energy minimization via graph cuts”.IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(11):1222-1239.
[11]王海英,黄强,李传涛,褚宝增.图论算法及其MATLAB实现[M].北京:航空航天大学出版社,2010.108-110.
[12]王朝瑞.图论[M].北京理工大学出版社,1997.275-284.
[13]Boykov Y.Veksler O.Zabih R.Siemens Corp.Res.,Princeton,NJ.Fastapproximateenergy minimization via graph cuts.IEEETransactionson Pattern Analysis and Machine Intelligence,2001,23(11):1222-1239.
Research on Improved Arithmetic of Neighborhood Mean Filtering
Niu Xiu-qin
(School of mathematics and science,Sichuan Normal University,Chengdu Sichuan 610066,China)
Neighborhood mean denoising algorithm as one method of image denoising algorithm,can not only effectively remove image noise,but also can be quickly smooth image.Meanwhile,it can make the image edge blur.First,this paper proposes new energy models based on Energy Minimization principle and Neighborhood mean filter,which is named Energy model,such as model E1 and model E2,and then,proposes a new Neighborhood Mean Denoising Filter.According to solve the local neighborhood energy minimum,two models judge whether pixel grayscale value is substituted.The new Neighborhood Mean Denoising algorithm not only change the single way of original neighborhood mean filter algorithm,but also reduce the possibility of the good pixels be mistaken for the noise pixels.Meanwhile,it can change the threshold free.This filter is particularly effective in suppressing Salt&pepper noise.
image denoising;mean filtering;energy minimization
TP391
A
1673-2014(2012)02-0004-05
2012—03—10
牛秀琴(1987—),女,山西运城人,硕士研究生,主要从事数字图像处理、模式识别研究。
(责任编辑 李学斌)

