双向地震下刚度偏心体系的弹塑性反应谱研究
王丰,武志东
(大连民族学院土木建筑工程学院,辽宁大连 116605)
双向地震下刚度偏心体系的弹塑性反应谱研究
王丰,武志东
(大连民族学院土木建筑工程学院,辽宁大连 116605)
针对实际地震动的多维性、偏心引起结构多分量反应的耦合作用以及结构非线性的空间耦合特性,建立了可考虑刚度偏心影响的单层体系弹塑性等延性拟强度折减系数谱。根据对硬、中、软三类场地60条地震动记录进行时程计算的结果,分析了不同场地类型、相对偏心距、扭转频率比等因素对拟强度折减系数谱的影响,为进一步建立可应用于工程实际的多维弹塑性设计反应谱奠定基础。
双向地震作用;弹塑性反应谱;刚度偏心;强度折减系数
在基于性能抗震设计中,弹塑性反应谱在计算结构地震位移反应方面越来越受到重视[1-4]。然而到目前为止,弹塑性反应谱的研究几乎都是以单自由度体系模型和单向地震输入为前提的,不考虑平面外的影响。以往震害的现象和分析表明,偏心结构在地震下除了产生平移振动外,还会围绕刚心作扭转振动,形成平扭耦联振动[5-6]。同时,结构在多维地震作用下还会形成非线性反应的空间耦合作用[7]。所以仅考虑地震的单向水平作用或按等效的单自由度体系来计算分析结构的弹塑性反应并不能准确反映实际情况。
本文建立了偏心单层体系的等延性拟强度折减系数谱,通过采用硬、中、软三类场地60条地震动记录进行时程计算的统计结果,分析了不同场地类型、相对偏心距、扭转频率比等因素对拟强度折减系数谱的影响。
1 刚度偏心体系的弹塑性谱反应理论
1.1 运动方程
设一个单层体系,它在相互垂直的两主轴x,y方向上和水平扭转方向上分别具有两水平平动自由度和一扭转自由度。沿x向和y向同时承受双向地震动作用,如图1。
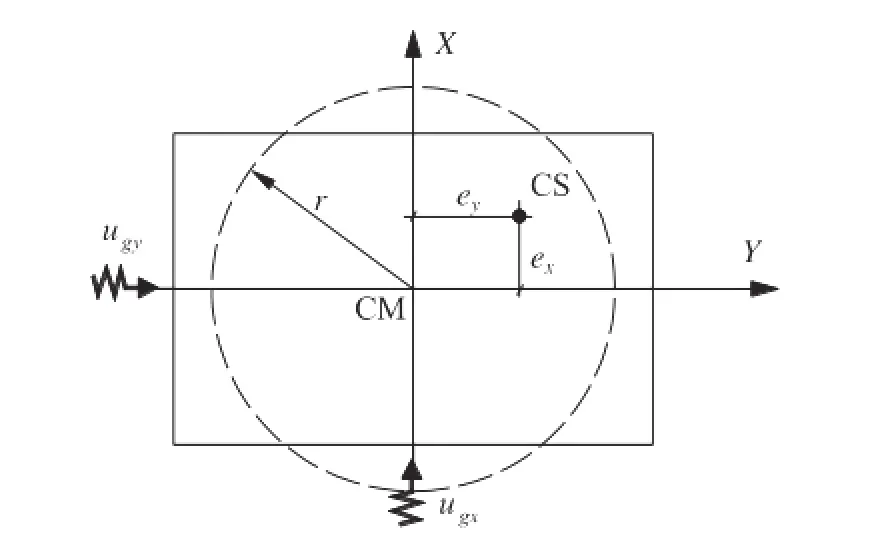
图1 刚度偏心单层体系平面布置图
弹塑性单层体系运动方程可以表示为
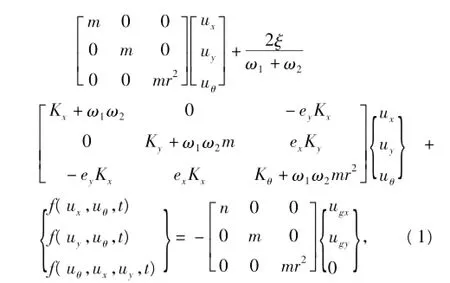
式中,ω、ω2分别为单层体系的第一、二自振频率;ξ为阻尼比;{uxuyuθ}T为单层体系三个自由度方向的位移向量;{ugxugy0}T为双向水平地震动输入时程向量;ex和ey分别为刚心的x轴和y轴坐标;Kx,Ky,Kθ分别为沿x,y向抗侧刚度和扭转向抗扭刚度;r为单层体系的回转半径;{f}T3为恢复力列向量。设uφ=r·uθ,并定义x向和y向相对刚度偏心距分别为ey/r和ex/r。整理式(1)有

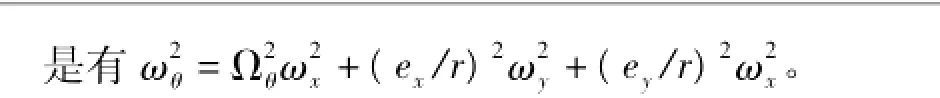
1.2 弹塑性计算
在地震作用下,由于结构偏心引起的扭转恢复力峰值与结构的纯扭强度相差很大,所以本文忽略了屈服函数中扭转恢复力项,定义偏心单层体系屈服准则为二维塑性屈服函数[9]:
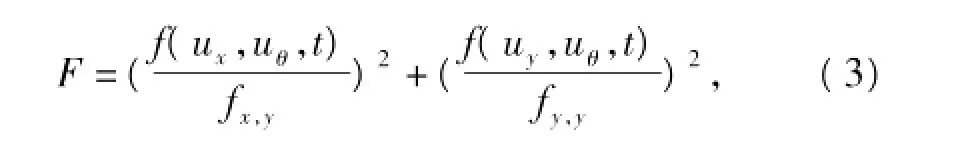
式中,fx,y和fy,y分别为x向和y向的单自由度屈服强度。
为便于研究,假定恢复力特性为理想弹塑性形式。本文通过弹塑性力学增量理论[10]来确定体系的切线刚度:当F<1时,单层体系处于弹性阶段,弹塑性切线刚度为

当F=1时,两水平自由度和扭转自由度运动耦合,发生屈服和塑性流动,弹塑性切线刚度阵为

1.3 拟强度折减系数反应谱
本文定义弹塑性单层体系x向和y向拟强度折减系数为

运用文献[9]的迭代思路,便可分别建立单层体系x向和y向的等延性拟强度折减系数反应谱、Rx-μx谱和Ry-μy谱。为了便于研究分析,仅考虑单向偏心情况,即建立x向的拟强度折减系数谱,有ex/r=0,ey/r≠0。根据对现存建筑结构统计结果[12],结构横纵两方向基本周期比一般在0.6~1.66之间,并且绝大多数结构两方向基本周期相等或接近。为此,以下分析中仅考虑两主轴方向基本周期相等情况的偏心及无偏心单层体系x方向弹塑性反应谱。
2 偏心体系弹塑性反应谱分析
2.1 地震记录的选取
按硬土、中硬(软)土和软土,每类场地选择10组双向地震记录,共30组。所选取的地震记录与文献[11]相同。因为仅建立x方向反应谱,为了在统计上更具合理性,对所选的双向地震动的两个分量与体系x,y两主轴方向进行组合。由于每组双向地震动在两个方向上会有两种组合方式,所以文中每种场地相当有20组双向地震动记录。
2.2 刚度偏心影响
扭转频率比为1时,不同相对刚度偏心距的单层体系在三类场地下延性系数μ为4的拟强度折减系数谱比较如图2(a)、图3(a)和图4(a)。从图中可以知道,对于扭转频率比为1的情况,随着偏心距的增大拟强度折减系数谱逐渐衰减;单层体系中,无偏心情况的拟强度折减系数谱最大,但其仍略小于单自由度强度折减系数谱。分析其原因:由于本文中拟强度折减系数和延性系数均定义为偏心耦合反应与单自由度反应之比的形式,考虑偏心耦合后的位移反应相对单自由体系反应明显放大,并随偏心增大而增大,而弹性加速度反应则增大幅度较小,甚至有减小趋势[11],所以等延性拟强度折减系数谱的谱值会随相对偏心距的增大而逐渐降低。
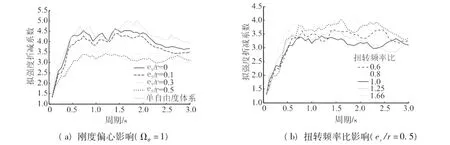
图2 硬土场地影响因素分析(μ=4)
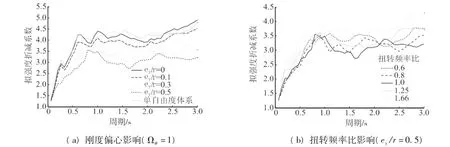
图3 中硬(软)土场地影响因素分析(μ=4)
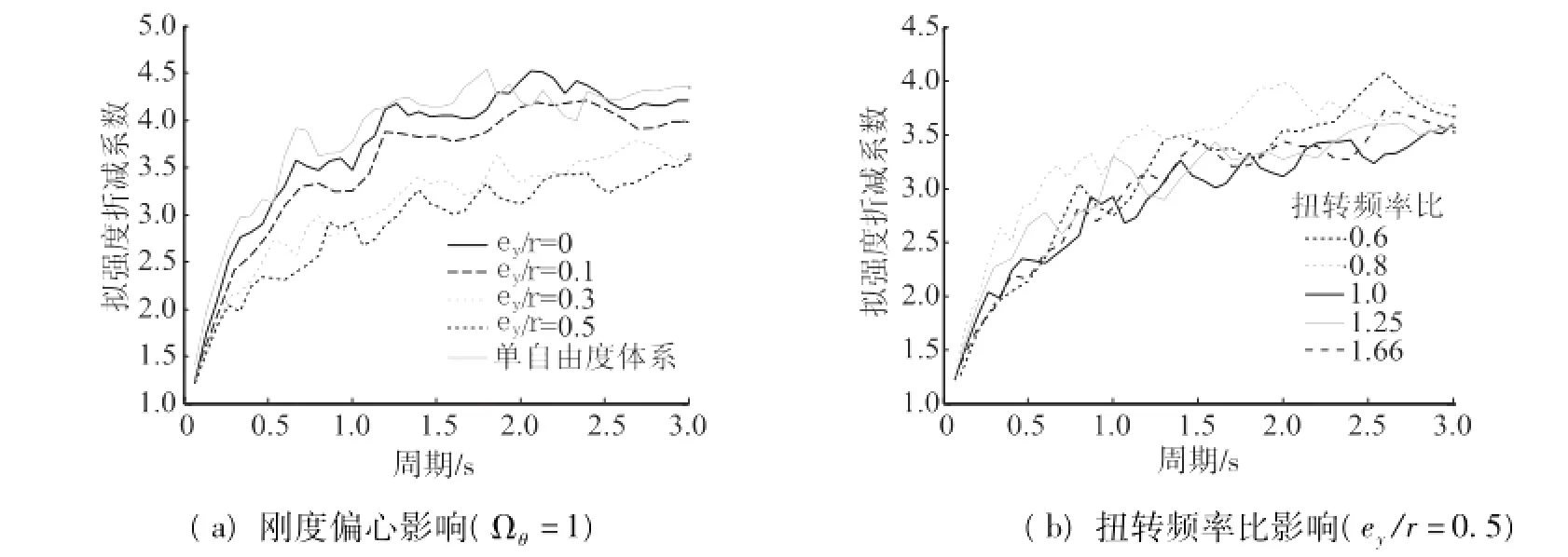
图4 软土场地影响因素分析(μ=4)
2.3 扭转频率比影响
扭转频率ωθ是考虑偏心耦合作用下结构反应的重要影响因素,本文以扭转频率比Ωθ作为参量来表示这一影响因素。以相对偏心距e/r=0.5为例,三类场地下扭转频率比分别为Ωθ=0.6,0.8,1.0,1.25,1.66的拟强度折减系数谱比较图如图2(b)、图3(b)和图4(b)。扭转频率比Ωθ= 1时,单层体系拟强度折减系数谱最小。随着扭转频率比向Ωθ>1或Ωθ<1的变化,拟强度折减系数谱逐渐增大,并且变化近似线形关系。
3 结论
为了建立可应用于多维抗震设计的偏心体系弹塑性设计反应谱,本文提出了双向地震作用下偏心体系的等延性拟强度折减系数反应谱。采用了二维屈服准则和弹塑性力学增量理论,通过硬土、中硬(软)土、软土三类场地30组双向地震动记录的时程统计结果,分析了不同扭转频率比、不同相对偏心距及不同场地类型的等延性强度折减系数谱。通过分析得出:(1)各类场地的拟强度折减系数谱均具有独自特征。(2)扭转频率比为1时,相对单自由度体系或无偏心单层体系,偏心单层体系的拟强度折减系数谱值衰减最为明显。随着扭转频率比的变化,这种衰减趋势逐渐减少。(3)当给定扭转频率比时,单层体系拟强度折减系数谱值随相对偏心距的增大而减小。
[1]FAJFAR P.Capacity spectrum method based on inelastic demand spectra[J].Earthquake Engineering Structural Dynamics,1999,28:979-993.
[2]RIDDELL R,GARCIA J E,GARCES E.Inelastic deformation response of SDOF systems subjected to earthquake[J].Earthquake Engineering Structural Dynamics,2002,31(3):515-538.
[3]徐福江,钱稼茹.常延性系数弹塑性位移谱及其应用[J].工程力学,2007,24(6):15-20.
[4]翟长海.钢筋混凝土规则框架结构非弹性位移比谱研究[J].工程力学,2009,26(9):80-86.
[5]李宏男.地震动的转动分量及有关的结构反应分析[J].世界地震工程,1991,(4):44-51.
[6]周晓松,裴星洙,廖述清.单层偏心结构平扭耦合地震反应分析[J].工程建设与设计,2005(3):56-60.
[7]李宏男.结构多维抗震理论[M].北京:科学出版社,2006.
[8]RAFAEL R,HERNAN S M.Inelastic response of onestorey asymmetric-plan systems subjected to bi-directional earthquake motions[J].Earthquake Engineering and Structural Dynamics,1999,28:273-285.
[9]王东升,李宏男,王国新.双向地震动作用的拟等延性系数谱[J].地震工程与工程振动,2004,24(4): 25-31.
[10]江见鲸.钢筋混凝土结构非线性有限元分析[M].西安:陕西科学技术出版社,1994.
[11]王丰,李宏男.双向地震动作用下刚度偏心单层体系弹性反应谱研究[J].振动与冲击,2007,26(6):4-9.
[12]包世华,方鄂华.高层建筑结构设计[M].北京:清华大学出版社,1998.
Study on Inelastic Response Spectra for Stiffness Asymmetric Systems Subjected to Bi-directional Ground Motions
WANG Feng,WU Zhi-dong
(College of Architecture&Civil Engineering,Dalian Nationalities University,Dalian Liaoning 116605,China,)
The strength reduction factor spectra of constant ductility factors for one–storey asymmetric plan system is presented considering the characters of multi-dimensional response of structures,torsion coupling response of structures and nonlinear spatial coupling of structural multi-components.The effects of normalized stiffness eccentricity,rotation frequency ratio for spectra amplitude on strength reduction factors are discussed based on statistic analysis of 60 recordings in two directions for hard site,medium site and soft site,which is the base for further forming the inelastic design response spectra of asymmetric systems in engineering application.
bi-directional ground motions;inelastic response spectra;stiffness asymmetric; strength reduction factor
P315.9;TU311.3
A
1009-315X(2012)03-0256-04
2012-01-03;最后
2012-02-23
国家自然科学基金项目(51108067);中央高校基本科研业务费专项资金资助项目(DC10040116);辽宁省教育厅高等学校科研项目计划(L2010098);住房和城乡建设部科技项目(2010-K3-55);大连民族学院人才启动基金资助项目(20086204)。
王丰(1976-),男,回族,辽宁沈阳人,副教授,博士,主要从事建筑结构抗震理论研究。
(责任编辑 邹永红)

