基于风险传播机制的集群抗风险能力研究
王娇俐, 王文平, 沈秋英
(东南大学经济管理学院,江苏南京210096)
基于风险传播机制的集群抗风险能力研究
王娇俐, 王文平, 沈秋英
(东南大学经济管理学院,江苏南京210096)
文章基于风险传播机制,从企业所属的网络出发,借鉴复杂网络的最新研究成果,研究网络社区结构对集群抗风险能力的影响。研究发现,网络的抗风险能力是社区度的“倒U型”函数,企业和政府据此可以有方向地管理和调节社区内与社区间连接来改变网络的社区度,使网络的抗风险能力最强,帮助集群企业提高应对风险的能力。
经济危机;复杂网络;平均场理论;抗风险能力
一、引 言
自2008年的全球金融危机以来,国际、国内市场和经济形势呈现出动荡加剧和不确定性增大的趋势,使我国内生型产业集群中大量中小型制造企业面临的风险剧增,如何发挥集群整体优势,提高抗风险能力,成为内生型产业集群企业迫切需要解决的问题。
Markusen曾指出产业集群越成功,则越倾向于发展成一个封闭的系统,进而逐步丧失应对市场变化的能力,导致其竞争力不断下降[1]。而此时集群如果遭遇来自集群外部的风险(外生性风险),则集群将有可能一蹶不振甚至消亡。集群的外生性风险主要包括结构性风险和周期性风险[2][3];同时,集群面临的内生性风险也是产业集群走向衰退的重要影响因素。内生性风险是指由企业集群内部联系得固化、同质化等所累积的风险。吴晓波等借用植物学的“自稔性”术语来形象地分析集群的内生性风险[4]。集群网络通过点和边的抽象可视为复杂网络,Harrison指出网络关系是一把双刃剑,企业间联系一方面是企业集群本质特征,同时网络力量也可能破坏集群的持续发展[5]。张荣佳也指出,企业网络的微观结构对产业集群的发展会产生重要影响[6]。王发明等用复杂网络理论中度分布、聚集系数以及平均最短路径长度作为刻画集群网络结构的变量,初步定性探讨了这些结构变量对集群网络风险的影响[7]。
近年来对复杂系统结构的研究除了小世界[8][9]、无标度特性外[10],还发现了复杂网络的一个新的统计特性:社区结构[11][12]。学者们通过观察发现,在网络中会出现一些点构成的点集,这个集合中的点相互之间的联系比集合外面的点的联系要紧密得多。由于集群内企业之间的可能存在的血缘、亲缘、地缘或者朋友关系、合作历史等原因,集群中某个企业比较偏向于与某几个企业进行合作,建立了长期、稳定的合作关系,于是在集群网络中出现了社区结构[13]。而集群企业间密切相互作用所形成的社区结构,对集群内、外部风险的形成和抵御具有重要影响。但现有研究中,关于社区结构对集群的抗风险能力会产生什么影响以及怎么调整集群社区度以提高集群的抗风险能力等问题缺乏研究。而这些问题的研究,对处于动荡生存环境中的小企业集群,如何调整企业间关系,优化自身网络结构,以提高抗风险能力具有重要的现实意义。
二、基于社区结构的风险传递模型
1.复杂网络的生成模型
内生型产业集群的突出特点是集群中的企业规模都较小,差别不大。因此,可将集群中的企业抽象为点,企业之间的联系抽象为边,若两个企业之间有联系,则在复杂网络中这两个节点之间有边相连,风险只在有边相连的节点之间传递,故本文不考虑节点之间的距离对风险传播的影响,同时也不考虑传播时间的影响。
社区结构是复杂网络的一个重要特征,本文定义社区度p=社区间节点之间的连接数/社区内节点之间的连接数[14]。复杂网络的集聚系数C=(1/N)×是节点i的ki个邻点之间的连接总数,聚集系数是衡量网络中与同一节点相连的两个节点也相连的概率[14]。通过动态调节社区特性大小p,及通过调整q间接改变集聚系数C来生成网络,,其度的分布P(k)由p控制(0<p<1),而P(k)与q无关[15]。由网络生成方法可知Ei与q成正比[16],故C~q,因此q控制着所生成网络的集聚系数C(0<q<1)。
2.风险传播机制
借鉴SIR模型[17][18][19],假设在风险传播过程中,集群网络中每个节点有三种状态(A,B,C),其中A是没有受到风险威胁;B是与某个受倒闭的节点相连,故受到风险威胁;C是没有有效排除风险而倒闭。假设β是倒闭的企业将该风险传播到与之相连的没有受风险威胁节点的传播概率,我们设定β=0.5对应于在企业之间的非正式关系上的风险传播概率,如信用风险通过社会关系、企业家之间的关系进行传播等;β=0.9对应于正式关系如合同、契约关系传播风险的概率。当集群受到风险冲击时,风险可能在正式关系上传播,也可能通过非正式关系传递,为了比较不同类型关系对风险传播的影响,本文假设风险通过单种关系类型传播,该假设本质上不影响模型结果的总体趋势。假定初始网络中只有一个倒闭的节点,该节点将风险以概率β传给它的邻接节点,这样随着风险的传播,网络中受风险威胁的节点逐渐增多。如果某节点与倒闭的节点相连而受到风险威胁,可以通过提高自身对外部环境的应变能力,削弱甚至是规避掉外部经济环境的波动所引起的衰退风险,则该企业不会因为风险而倒闭;相反,如果受到风险威胁的企业,没有采取切实有效的动作或措施抵御风险,则该企业会倒闭,故假定从状态B到状态C的概率为γ。这样在风险传递的初期,处于B状态的节点会逐渐增多,直到时刻τ,当网络中处于B状态的点数目不再变化时,风险传递过程结束。
在一个度均为k,集聚系数为C的网络中,若β=1,则倒闭的节点首先将风险传递给k个点,接着由这些点传播给k(k-1-2E/k)个点(E是这k个点之间的边的数目),又C=2E/(k(k-1)),故k(k-1-2E/k)=k(k-1)(1-C),当C=1时,风险传播过程在第一步(t=1)即结束。因此,假定f(C)是集聚系数C对风险传递速度的影响函数0。因为不同度的节点传播风险的能力有所不同,假定Ak(t),Bk(t),Ck(t)分别是度为k的节点中处于不同状态的点的数量占总数的比例。运用动态物理中的平均场理论[20],有如下方程组成立:


三、模型结论与参数分析
1.模型结论
为了考察不同的参数取值对仿真结果的影响,利用MATLAB,分别在q=0.1,0.5,0.9时生成网络,并且选取不同风险传播概率(β=0.5,0.9)进行仿真。通过对仿真结果的绘图及图形分析发现,网络的社区度p,网络结构参数q,风险传播概率β对网络的抗风险能力均有影响,具体如图1和图2所示。当p≪1说明这个网络中的社区结构明显,网络被分成几个社区,社区内节点链接非常紧密,社区间联系十分稀疏,出现节点“扎堆”的现象。

图1 β=0.5,分别q=0.1,0.5,0.9时,AntiR和p的关系
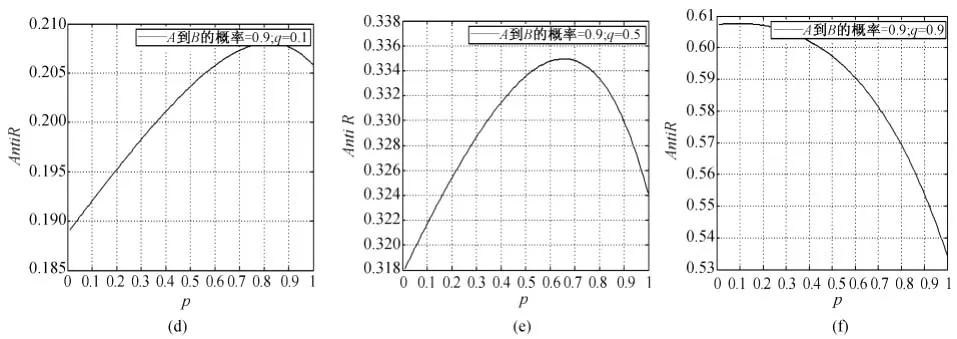
图2 β=0.9,q分别=0.1,0.5,0.9时,AntiR和p的关系
2.参数分析
模型结论(1):当q=0.1,0.5时,网络的抗风险能力AntiR不是关于社区程度p的单调函数,AntiR与社区度p呈“倒U型”的变化曲线,如图1中(a),(b)与图2中(d),(e)所示。具体地,AntiR先随p的增大而增大,当p到达一定数值时,AntiR达到最大,随后AntiR随p的增大而减小。
模型结论(2):当q=0.9,因为网集聚系数C与q成正比,故此时网络中的集聚系数C很大,集群网络的抗风险能力是社区度的减函数,如图1中(c)和图2中(f)所示。
网络的集聚系数C很大时,即表示网络中与同一个节点相连的两个节点之间相连的概率很大,社区间的联系是通过分别处于不同社区内的节点连接。在较小的社区度下,强集聚系数对于社区之间建立连接帮助不大,但有利于社区内部增加连接。当集群网络受到风险冲击,风险容易在某个社区内部蔓延,由于社区间连接很少,风险不容易从一个社区传递到另一个社区。因此,从整个网络的角度出发,受风险威胁的节点相对少一些,整个网络呈现较强的抗风险能力。而当网络的社区度逐渐增加,社区之间的连接变得紧密,同样由于网络的高集聚系数,社区间通过与同一节点相连而连接的可能性变大,使得社区间的联系变得频繁。当某个社区内节点倒闭而将该风险传递到其他社区的概率变大时,风险迅速在整个网络中传播,因此从集群网络整体出发,网络的抗风险能力降低。
模型结论(3):当网络的q相同,风险在不同类型的关系(非正式关系和正式关系)上传递,分别对应β=0.5(见图1中(a)与图2中(d))及β=0.9(图1中(b)与图2中(e))。分别比较这两组图可以发现,曲线的最高点对应的p随β的增大发生右移。
模型结论(4):当风险以一定的概率β在不同的网络上(q=0.1及q=0.5)传递,比较图1中(a)与(b),及图2中(d)与(e)可以发现,集群网络的抗风险能力达到最高点时对应的社区度p随q的增大发生左移。
四、结论及对策建议
当前形势下,广东、浙江、江苏等地由出口导向型中小企业组成的集群面临着由于国际性经济波动而带来的外生性风险影响,但外生性风险通常是集群发生危机的诱发性因素,只有自身反应僵化的集群才最终成为外生性风险的受害者。系统的结构决定系统的功能和运行方式[21],集群网络的社区结构是网络结构的重要方面,影响网络的运行效率。研究表明,这类中小企业组成的集群存在次级集群或小团体(即本文定义的社区)[22][13](P1105),这些团体往往以血缘为纽带,并扩展到亲缘、地缘关系,或者说集群网络已经具有社区结构的特性,即0<p0<1。分别对应上述模型结论,针对不同的情况,本文提出了集群层面提高抗风险能力的对策:
(1)根据当前集群网络的实际情况,结合模型结论(1),有方向、有目的地改变企业之间的链接,提高网络的抗风险能力。
若当前网络的社区度p0<p*,说明社区内企业之间的链接与社区间的链接相比太过稠密,可能会带来两方面的后果。一方面,企业结点过度限制于社区中,会导致“过度根植性”,不利于异质性信息的流动和获得全面的市场信息,即导致社区内知识趋于同质化;反过来,网络会变得僵化,形成合作社区的锁定效应,无法适应外部环境的变化,最终导致集群衰败。另一方面,这样的结构形成带有强烈本地特色的网络氛围,使得网络的弹性更为降低,因环境发生改变而需要对彼此之间的联结状态做出变革更为困难,集群抗风险能力进一步降低。根据模型结论,在这种情况下应该有意识地增加社区间的链接,促进异质信息的传播,首先有利于企业的学习和创新,增强企业应变的能力;其次有利于企业获得全面、及时的市场信息,帮助企业抓住时机,实施合理的发展策略,以应对当前的经济形势的变化。此外,不同社区间开展全方位的战略合作,利用各自的领先地位、知识差异、先进的技术以及丰富的经验,整合、利用市场需求和客户资源共同应对风险,提高网络的抗风险能力。
若当前网络的社区度p0>p*时,表明企业社区间的链接与社区内的链接相比过于稠密,则应当适当加大社区内企业之间的联系。一是较高内聚性的网络特征可以为社区内成员提供了许多面对面的交流机会,各类信息特别是隐性知识可以在社区成员之间得到较为广泛的传播,有利于促进企业学习以及创新,提高企业应对外部变化的能力。二是通过社区内合作解决问题,能够达到更大范围的适应性。比如当某个企业接到大订单,自己又无法按期完成的情况下,由于社区内企业之间的认知距离及社会距离比较小,建立联系的成本也比较低,企业往往可以根据信任关系将订单部分交给社区内的其他的企业完成,这样可以充分利用市场需求,化解困难。特别是在当前由经济危机导致的市场萎缩情况下,这种合作解决问题的机制有利于集群内企业充分利用市场需求,顺利度过难关。
(2)在集聚系数较大的网络中,一方面政府可制定相关的政策和法规来引导企业行为,其次企业也可通过自发地调节个体行为,减小集群网络的社区度以获得较好的抗风险能力。
当网络结构参数q很大,说明此时网络的集聚系数C比较高,由模型结论(2)可知,集群的抗风险能力是社区度的减函数。为了使集群具有较强的抗风险能力,则应增加社区内企业间的连接,减少社区间的链接,使得风险尽量在社区内传递,减小其在社区间甚至整个网络内的蔓延。
(3)政府和地方机构作为企业间交往的中介[22],可以根据最优社区度p*的位置,结合风险传播的机制,对当前的集群网络进行有目的、有方向的管理。
由模型结论(3)中最优社区度的分布位置可知,当集群遭遇的市场不确定性风险是在非正式关系网络中传播,那么应当通过组织企业社区内的交流、座谈等方式加强企业社区内的合作以减小社区度,尽量在社区内部通过非正式关系化解风险。而当风险是通过正式关系传递时,则应该尽量增加企业社区间的联系来增大社区度,通过调动网络中广大企业的力量来抵御、抗击风险。
(4)政府和地方机构还可以根据不同集群抵御风险的经验进行关系管理。比如当风险在某种关系(非正式关系或正式关系)网络中传递,假定有两个集群:集群1与集群2,集群1的集聚系数>集群2的集聚系数,则集群1内的氛围更为活跃,网络中的信息流动较畅,相互间信任度比较高,若此时网络2的社区度为p2,表现出很好的抗风险能力,则根据模型结论(4),网络1可参照网络2的情况,政府及地方机构可有方向地调节企业社区间及社区内的连接,使得网络1的社区度p1<p2,网络1的抗风险能力才有可能达到最优。
[1]MARKUSEN A.R.Sticky places in slippery apace:a typology of industrial districts[J].Economic Geography,1996,72:293-313.
[2]刘满凤.高技术产业集群中技术创新与扩散的系统基模分析与政策解析[J].科技进步与对策,2011,28(24):65-69.
[3]FRITZ O M,MAHGINGER H,VALDERRAMA M T.A Risk-oriented analysis of regional clusters[A].STERINER M.Clusters and Regional Specialization[C].London:Pion,Ltd.,1998.180-191.
[4]吴晓波,耿帅.区域集群自稔性风险成因分析[J].经济地理,2003,23(6):726-730.
[5]HARRISON B.The italian industrial district and the crisis of co-operative from:part 1[J].European Planning Studies,1994,2(1):3-22.
[6]张荣佳,原毅军.产业结构调整的微观基础:基于网络组织的分析[J].大连理工大学学报(社会科学版),2011,32(2):27-31.
[7]王发明,蔡宁,朱浩义.集群网络结构和风险研究[J].中国地质大学学报(社会科学版),2006,(6):22-26.
[8]WATTS D,STROGATZ S.Collective dynamics of smallworldnetworks[J].Nature,1998,393:440-442.
[9]WATTS D.Dynamics and the small-world phenomenon[J].A-merican Journal of Sociology,1999,105(2):493-527.
[10]BARABASI A L,ALBERT R.Emergence ofScaling in Random Networks[J].Science,1999,286:509-512.
[11]RADICCHI F,CASTELLANO C,CECCONI F,etal.Defining and Identifying Communities in Networks[J].Proc Natl Acad Sci USA,2004,101:2658-2663.
[12]PALLA G,DERENYI I,FARKAS I,etal.Uncovering the overlapping community structure of complex networks in nature and society[J].Nature,2005,435:814-818.
[13]SHEN Q Y,WANG W P.The evolution of company network based on the reputation’s grey dynamics[M].Nanjing:IEEE International Conference on Grey Systems and Intelligent Services,2007.
[14]刘军.社会网络分析导论[M].北京:社会科学文献出版社,2004.19.
[15]LIU Z H,HU B B,Epidemic spreading in community networks[J].Europhys.Lett,2005,72(2):315-321.
[16]WU X Y,LIU Z H.How community structure influence epidemic spread in social network[J].Physica A,2008,387:623-630.
[17]LIU Z H,LAI Y C,YE N.Propagation and immunization of infection on general networks with both homogeneous and heterogeneous components’[J].Physical Rev,2003,1-5.
[18]ZHENG D F,HUI P M,TRIMPER S,etal.Epidemics and dimensionality in hierarchical networks[J].Physica A,2005,252(2-4):659-668.
[19]PASTOR-SATORRAS R,VESPIGNANI A.Epidemic spreading in scale-free networks[J].Phys Rev Lett,2001,86:3200-3203.
[20]BARABASI A L,ALBERT R,JEONG H.Mean-field theory for scale-free random networks[J].Physica A,1999,272:173-187.
[21]陈胜,吴广谋.扁平化组织结构抗风险的分析[J].东南大学学报(哲学社会科学版),2002,10(4):13-16.
[22]McEVILY B,ZAHEER A.Bridging ties:a source of firm heterogeneity in competitive capabilities[J].Strategic Management Journal,1999,20(12):1133-1156.
Study of Industrial Cluster’s Ability to Resist Risk Based on Risk’s Transmission Mechanism
WANG Jiao-li, WANG Wen-ping, SHEN Qiu-ying
(School of Economics and Management,Southeast University,Nanjing 210096,China)
From clusters’network structure and based on the latest progress in complex network research,this paper focuses on the effects of the community structure on cluster’s ability to resist risk.It is found that the relationship between network’s ability to resist risk and community degree follows an inverse U-shaped curve.Accordingly the enterprises and governments can manage and adjust the links in the community and between communities in order to have the best ability to resist risk and help enterprises survive from the crisis.
economic crisis;complex network;mean-field theory;abilityto resist risk
F121.3
A
1008-407X(2012)01-0060-05
2011-05-11;
2011-07-24
国家自然科学基金项目(70973017;70571013);教育部人文社会科学规划项目(09YJA630020)
王娇俐(1976-),女,浙江余姚人,东南大学经管学院博士研究生,主要从事产业集群升级、区域经济研究。

