利用概率松弛法的城市路网自动匹配

张云菲，杨必胜，栾学晨

1.武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉430079；2.武汉大学 时空数据智能获取技术与应用教育部工程研究中心，湖北 武汉430079

1 引 言

随着传感器技术与地球空间信息科学的发展，空间数据的采集、建模、融合、更新等正处于快速发展时期。实际应用中常需要对不同设备、不同部门采集的同一地区的多源、多尺度空间数据进行有效集成，以用于信息共享与变化检测。空间数据匹配是实现空间数据变化检测和更新的前提条件，其目的是建立同一区域内两份或多份数据间同名目标的对应关系，通过这种对应关系可以实现两者的属性共享和几何精度改进［1－2］，亦可对无对应关系的目标进行变化检测和数据更新［3］。众源（crowdsourcing）地理数据，如欧洲的“开放式道路地图”（open street map，OSM）的出现，为空间数据的更新提供新的、免费的数据源。然而，由于其生产过程非标准化，众源数据匹配给传统的空间数据匹配方法带来新的挑战。

文献［4］对空间数据匹配的研究现状进行了系统的总结。对路网匹配而言，部分学者通过计算与候选路段间的几何、拓扑、语义等相似性特征选取最优的匹配路段［5－9］。多源空间数据之间通常存在非刚性偏差，通过几何、拓扑、语义等相似性可以确定多条可能的候选路段，但很难进一步确定实际的匹配路段，因此，需要考虑在整个路网中与其他匹配对之间的兼容性。一些学者将相似性指标融合成概率或其他综合指标，考虑邻接目标的匹配关系更新自身匹配概率［10－13］。文献［11—12］尝试利用概率松弛法解决矢量道路匹配问题，实现了1∶1的道路节点对应，但需要进一步建立路段间的对应关系，文献［13］将概率松弛法直接应用于路段，需要设定多种阈值，且匹配概率受路网密度影响较大。文献［11—13］忽略1∶0匹配，即无对应关系的独立路段，这些独立路段是潜在的变化检测目标。另外，由于OSM等众源数据的非标准化表达方式以及内部尺度不一性，以不同数据作为参考得到的结果不一（即存在匹配方向性问题），且1∶N、M∶N的对应关系很难有效识别。

概率松弛匹配方法在计算机视觉和模式识别领域是一种经典的图匹配方法［14］，该方法首先对两份图结构建立初始匹配矩阵，再结合邻域目标的结构关系启发式地更新初始的匹配矩阵使之达到全局最优。城市道路网是一种复杂的图结构，实现路网匹配需要综合考虑位置、形状、结构等特征，采用概率松弛法能够将多种约束有效结合，实现路网的整体匹配，而不是局部映射。因此，本文在改进文献［13］的概率和兼容函数计算模型基础上提出一种基于概率松弛法的城市路网自动匹配方法，该方法能够建立1∶0的匹配关系，减少阈值和路网密度的影响。最后，本文选取不同地区的两份路网数据进行算法验证。

2 基于概率松弛法的自动匹配方法

根据文献［11—13］，概率松弛匹配方法包括概率矩阵初始化和迭代更新两个基本过程。本文考虑路网的复杂性增加了匹配结果选取过程，具体算法流程如图1所示，主要分为3步：①利用缓冲分析检测候选匹配路段，然后根据候选路段间的几何差异指标计算不同匹配方向的概率并综合得到初始概率矩阵；②由于初始概率未考虑邻接路段对其的兼容程度，即兼容系数，本文通过邻接路段间的相对关系计算两邻接匹配对的兼容系数，并基于各邻接匹配对的兼容系数计算所有邻接路段对其的综合影响，即支持系数，然后根据支持系数不断更新原概率矩阵，直到概率矩阵变化量收敛于某一极小值；③计算各候选匹配对的结构相似性，结构相似性反映某一匹配对及其邻接路段间的整体匹配程度，之后基于结构相似性设定一定规则选取稳健匹配集，识别1∶1和1∶M，并对1∶M进行匹配增长，综合得到最后匹配集。

图1 本文算法流程Fig.1 Flow chart of the proposed method

2.1 概率矩阵初始化

假设待匹配两份数据data1＝｛N1，E1｝，data2＝｛N2，E2｝，其中N代表端点集，E代表路段集。本文首先通过缓冲分析确定data1与data2之间的候选匹配路段，再计算候选路段间的差异性指标并综合得到初始的概率矩阵。差异性指标是描述两候选路段间差异的指标，评价线性目标的差异性指标有距离、方向、长度、语义、拓扑等［5－7］，本文采用距离、方向、长度衡量路段间差异特征。对一种差异性指数t（t＝dis，dir，len，分别表示距离，方向，长度差异性指标），根据文献［10］按公式（1）计算路段j∈N2匹配到路段i∈N1的概率pti（i，j）。当j＝ －1时，pti（i，－1）表示路段i匹配到空（1∶0）的概率

式中，CSi为路段i的候选匹配路段集；dt（i，j）为路段i和j间差异性指标t的值；β1t为关于差异性指标t从data2到data1的误差因子，用于计算1∶0的匹配概率，文献［13］未考虑1∶0匹配关系，导致独立路段误匹配至最近的路段。本文通过计算两份数据间Hausdorff距离估算误差因子，公式为

同理，计算从data1到data2的误差因子βt2和路段i匹配到路段j的概率ptj（i，j）。实际上，匹配概率应为两路段相互匹配的概率，即i匹配到j且j也匹配到i的联合概率。因此，需将不同方向匹配的概率综合为相互匹配概率，公式如下

候选匹配对（i→j）的概率定义为不同匹配方向概率的调和平均数［15］。i没有匹配路段的概率pt（i，－1）定义为i匹配到空且所有候选路段不匹配到i的概率，同理，j没有匹配路段的概率为pt（－1，j）。

为综合多种差异指标［6］，本文分别计算3种差异指标的匹配概率，加权平均得到综合的初始概率。距离、方向、长度的权值分别为0.3，0.4，0.3。

2.2 概率矩阵迭代更新

初始概率矩阵确定以后，需计算各匹配对的邻接路段对其的兼容系数以不断更新原概率矩阵。兼容系数反映了邻接匹配对间的兼容程度，而通常邻接匹配对不止一个，需要综合这些邻接匹配对的影响，即支持系数来改进初始概率矩阵，使之更准确地反映整个路网的匹配关系。另外，考虑到路段匹配可能存在部分匹配，即1∶M，而根据一定的距离或长度比阈值很难有效识别这类型匹配。如图2（a），路段a1和b1的长度，起终点距离皆相同，根据文献［13］将被误识别为1∶1匹配，而实际匹配应为（a1→b1，b2）。因此，需要考虑部分匹配对自身的兼容性。

图2 部分匹配与兼容系数计算Fig.2 Partial matching and calculation of the compatibility coefficient

基于文献［12］，本文考虑邻接路段的相对位置，方向计算兼容系数，一定程度上克服数据本身的旋转和缩放误差。如图2（b）所示，计算邻接匹配（h→k）对（i→j）的兼容系数C（i，j；h，k），公式为

式中，ratio为点o到e的路段长度与o′到e′之间长度的比值；δdis和δdir分别为路段i、h与j、k之间的位置和方向一致性指标，计算公式如下

d1和d2分别为点o、o′和e、e′的距离；α（β）为路段i与h（j与k）的夹角，β1dir（β2dir）与β1dis（β2dis）为公式（2）计算的位置和方向误差因子。对于自兼容性，如C（i，j；i，k），首先在路段i上寻找中间节点o′的对应点o，再按公式（5）计算兼容性，同理计算C（i，j；h，j）

而某一候选匹配对的概率受到多个邻接匹配对的影响，需要综合所有邻接匹配对的影响以计算支持系数。如图3所示，对于候选匹配对（i→j），F1，F2和T1，T2分别为对应起点和终点，相应的，SF、QF和ST、QT为i和j在起点和终点处的邻接路段集。如表1所示，不同匹配方向的支持系数皆由起点、终点处支持系数构成，q1和q2为（i→j）是完全匹配和部分匹配假设下的支持系数，本文取两者中较大值。

图3 计算支持系数Fig.3 Calculating the support values

表1 支持系数计算Tab.1 Calculation of sub－support values

例如，当j匹配到i时，在起点的支持系数qi，F为

式中，r为迭代次数；C为计算的兼容系数；p（r）为第r次迭代时概率。同理可计算在终点处的支持系数qi，T以及i匹配到j时在起点、终点处的支持系数qj，F、qj，T。将起终点处支持系数相加得到j匹配到i以及j匹配到i的支持系数q（r）i和q（r）j，再按公式（7）综合得到最后的支持系数q（r）。

ηi为i匹配到空的先验值，计算公式为

最后根据文献［11］提出的迭代机制重新计算概率，以路段j匹配到i为例，公式为

根据不同匹配方向计算的概率按类似公式（3）综合得到新的概率矩阵。如此迭代，直到概率矩阵变化量小于某一给定阈值ε。

2.3 匹配对选取

为有效克服误匹配和漏匹配，本文设定以下3步用于匹配对的选取。

第1步：计算结构相似性。结构相似性反映某一匹配对及其邻接路段间的整体匹配程度，本文定义候选匹配对（i→j）的结构相似性为

式中，strF、strT分别为对应起终点处的结构相似性。假设SF、QF分别为i和j在起点处的邻接路段集，根据二分图匹配算法［16］计算两者间的最大匹配，strF即为该匹配组合下的概率之和，同理计算strT。为减少计算量，本文对迭代后概率矩阵按大律法［17］对行和列二值化，两者相加将概率矩阵分为3级，本文排除第3级候选匹配对，只计算前两级的结构相似性。

第2步：选取稳健匹配对。若（i→j）满足等式（11），则（i→j）为稳健匹配对，添加到队列queue中。

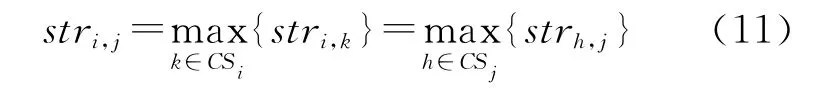
之后，需逐一检测queue中每一匹配对与邻接匹配对是否兼容。如图4所示，当两邻接匹配对Mn，Mp的中间结点（a2，b2）不同时是Mn或Mp的对应端点，则认为Mn、Mp相互不兼容。对于不兼容的两邻接匹配对，本文保留结构相似性大的，删除结构相似性小的。

图4 邻接匹配对之间的兼容性检测Fig.4 Detecting the compatibility between two neighbouring matching pairs

第3步：检测1∶M匹配对。对于queue中每一匹配对，判断其对应起点和终点是否皆匹配，如果匹配，则为1∶1对应，否则应为1∶M匹配。判断匹配对（i→j）在某对应端点处是否匹配，应满足以下条件：①若（i→j）在对应端点处的结构相似性大于i和j的其他匹配对在该对应端点处的结构相似性；②（i→j）在该对应端点处的邻接匹配对中至少存在一匹配对M∈queue。

若（i→j）在某对应端点处满足条件①和②，则认为（i→j）在该对应端点处是匹配的。如果（i→j）的对应起点和终点皆匹配，则该匹配对为1∶1匹配，否则为1∶M的匹配。逐一检测queue中的每一匹配对是否1∶M的匹配对，若是，则添加到临时队列temp。

逐一遍历temp中的每一匹配对，如图5中（i→j），若起点不匹配，则从短路段i的起点开始，遍历其邻接路段集G＝｛g0，…，gk，…，gn｝，从中选择与j的结构相似性最大的gk，添加新的匹配对（gk→j）到queue，再从gk的邻接路段中寻找与j的结构相似性最大的路段，组成新的匹配对添加到queue中，如此循环直到找到j的起点的匹配端点。若（i→j）的对应终点也不匹配，则进行同样的匹配增长过程。进行完匹配增长后，对新的queue中每一匹配执行第2步中的兼容性检查，同样保留结构相似性大的，删除结构相似性小的。

图5 匹配增长过程Fig.5 Matching growing from unmatched nodes

3 试验与评价

本文选取中国武汉，瑞士苏黎世的两份路网数据进行匹配算法的验证。武汉为四维图新（NavInfo®）导航数据与OSM数据匹配，苏黎世为NAVITEQ®导航数据与OSM数据匹配，空间参考为WGS－84，各数据的节点、路段统计如表2所示。导航数据格式为＊.shp，OSM数据格式为＊.osm，首先利用FME将OSM数据转换为统一的＊.shp，并通过 Microsoft Visual Studio 2008（C＃）＋ArcGIS Engine 9.3实现本文匹配算法，其中武汉、苏黎世的缓冲距离分别设为200m和40m，迭代终止阈值设为0.000 5。

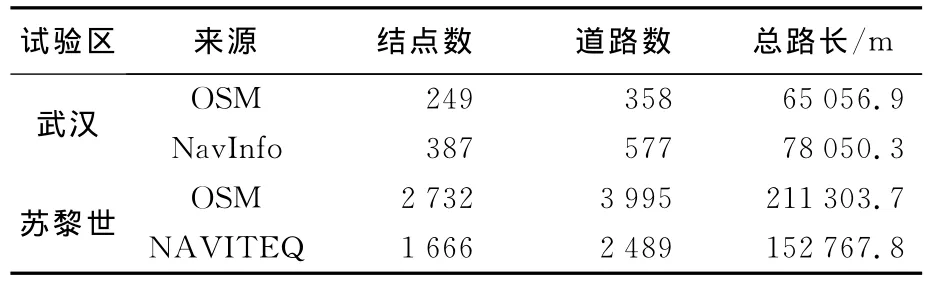
表2 路网数据统计描述Tab.2 The statistical description of road networks

试验的部分结果如图6所示，黑实线为导航数据，灰实线为OSM数据，虚线为匹配路段的中点连线，其中图6（a）、（b）为武汉地区试验结果，图6（c）、（d）为苏黎世地区试验结果。由图6（a）可见，对于武汉地区，OSM数据由于配准精度不高，与专业的导航电子数据的偏差达上百米，而本文方法可以有效地克服这种偏差实现整体匹配最优，图中虚线椭圆中匹配的两条路段位置不是最近的；图6（b）说明本文方法能够较好地匹配复杂路网结构。图6（c）中，OSM数据在某些区域要比导航数据详细，将OSM数据匹配到导航数据或反过来，得到的匹配结果不同，本文方法不受匹配方向影响，有效避免独立道路误匹配到另一份数据中最相似道路。图6（d）表明本文能有效处理众源数据中可能存在结构不完整的路网，虚线椭圆中OSM路段由于用户编辑错误导致连通道路断开。

图6 试验匹配结果Fig.6 The matching results

为定量评价本文算法的匹配精度，通过与人工匹配对比，计算匹配的准确率P和召回率R公式为

式中，TP为正确匹配数；FP为错误匹配数；AM为人工无法判断的匹配数；FN为漏匹配数。统计结果如表3所示，两试验区的匹配精度均达到96%以上，召回率也达到于90%以上，但还有5.3%～8.8%的匹配对未能有效被识别。为分析本文算法的效率，表3统计了单次迭代耗时，武汉为4s（8580候选匹配对），苏黎世为30s（22559候选匹配对），这是由于苏黎世路网密度比武汉高，落在缓冲区中的候选路段相对多导致计算量大。实际上，总匹配耗时受如试验范围、数据详细程度、路网密度、缓冲阈值、收敛条件等多种因素的影响。

表3 匹配结果统计Tab.3 Statistics of matching results using the proposed method

如图7所示，通过缓冲分析确定灰色的路段a1、a2的候选路段，分别统计迭代过程中路段a1、a2与各候选路段的概率变化，如图8（a）和（b）所示。由图8（a）可见，相比a1的其他候选路段，a1与c2的初始概率最高，且在迭代过程中仍保持较高概率，并收敛于某一稳定值；由图8（b）可见，虽然a2与d1、d2的初始概率最高，但通过不断迭代，a2与d4、d5的概率达到最高并收敛于某一稳定值。结果表明，本文方法结合邻接路段的匹配关系对概率矩阵进行迭代更新，可以帮助寻找正确的匹配路段，并有效降低误匹配率。

图7 迭代过程举例Fig.7 The matching examples for relaxation

为分析本文方法对参数的敏感度，本文设定5组缓冲距离（100m，150m，200m，300m，and 400m）对武汉地区进行多次试验，试验结果中的正确匹配，错误匹配，模糊匹配数目统计如图9所示。由图可见，阈值设为150m至400m之间时，匹配精度大约为95.4%～97.2%，而当阈值为100m时，精度降为67.4%，说明本文方法一定程度上不受阈值的影响，可以达到95%以上，但使用较小的阈值导致不能完全检测可能的匹配路段，使匹配精度降低。为取得较高匹配精度，建议使用稍大的阈值，然而，过大的阈值将导致计算时间的增加。

图8 迭代过程中概率变化Fig.8 Matching probability change during iteration

图9 不同缓冲阈值下的精度比较Fig.9 Matching precision of different buffering thresholds

4 结 论

本文方法考虑自身的几何相似性以及邻接候选匹配路段的兼容性，迭代计算候选路段的匹配概率，最后基于收敛的概率矩阵选取最后的匹配结果。试验结果表明，该方法对偏差较大的路网数据能达到较高的匹配精度，不存在匹配方向性问题，且能够识别1∶0和1∶M的匹配关系，该方法适用于偏差较大、存在一定尺度差异的路网数据，可用于存在不完整拓扑的众源路网与专业数据的集成，同时为路网更新和变化发现提供了关键技术支撑。未来的研究将侧重于计算效率的改进，基于匹配关系的变化提取和数据更新。

［1］ SAALFELD A J.Conflation：Automated Map Compilation［J］.International Journal of Geographical Information Systems，1988，2（3）：217－228.

［2］ ZHANG Meng.Methods and Implementations of Roadnetwork Matching［D］.Munich：Technical University of Munich，2009.

［3］ HU Yungang，CHEN Jun，ZHAO Renliang，et al.Matching of Roads under Different Scales for Updating Map Data［J］.Geomatics and Information Science of Wuhan University，2010，35（4）：451－456.（胡云岗，陈军，赵仁亮，等.地图数据缩编更新中道路数据匹配方法［J］.武汉大学学报：信息科学版，2010，35（4）：451－456.）

［4］ RUIZ J J，ARIZA F J，UREA M A，et al.Digital Map Conflation：A Review of the Process and a Proposal for Classification［J］.International Journal of Geographical Information Science，2011，25（9）：1439－1466.

［5］ COBB M A，CHUNG M J，FOLEY H I，et al.A Rulebased Approach for the Conflation of Attributed Vector Data［J］.GeoInformatica，1998，2（1）：7－35.

［6］ VOLZ S.An Iterative Approach for Matching Multiple Representations of Street Data［C］∥Proceedings of the ISPRS Workshop on Multiple Representation and Interoperability of Spatial Data.Hanover：ISPRS，2006：101－110.

［7］ MUSTIÉRE S，DEVOGELE T.Matching Networks with Different Levels of Detail［J］.Geoinformatica，2007，12（4）：435－453.

［8］ XIONG D，SPERLING J.Semiautomated Matching for Network Database Integration ［J］.ISPRS Journal of Photogrammetry ＆Remote Sensing，2004，59（1）：35－46.

［9］ SAMAL A，SETH S，CUETO K.A Feature－based Approach to Conflation of Geospatial Sources［J］.International Journal of Geographical Information Science，2004，18（5）：459－489.

［10］ SAFRA E，KANZA Y，SAGIV Y，et al.Location－based Algorithms for Finding Sets of Corresponding Objects over Several Geo－spatial Data Sets［J］.International Journal of Geographical Information Science，2010，24（1）：69－106.

［11］ ZHAO Dongbao，SHENG Yehua.Research on Automatic Matching of Vector Road Networks Based on Global Optimization［J］.Acta Geodaetica et Cartographica Sinica，2010，39（4）：416－421.（赵东保，盛业华.全局寻优的矢量道路网自动匹配方法研究［J］.测绘学报，2010，39（4）：416－421.）

［12］ SONG W，KELLER J M，HAITHCOAT T M，et al.Relaxation－based Point Feature Matching for Vector Map Conflation［J］.Transactions in GIS，2011，15（1）：43－60.

［13］ ZHANG Yunfei，YANG Bisheng，LUAN Xuechen.Automated Matching Road Networks Based on Probabilistic Relaxation［C］∥Proceedings of ISPRS Workshop on Dynamic and Multi－dimensional GIS.Shanghai：ISPRS，2011：75－80.

［14］ CHRISTMAS W J，KITTLER J，PETROU M.Structural Matching in Computer Vision Using Probabilistic Relaxation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1995，17（8）：749－764.

［15］ HUNTINGTON E V.Sets of Independent Postulates for the Arithmetic Mean，the Geometric Mean，the Harmonic Mean，and the Root－mean－square［J］.Transactions of the American Mathematical Society，1927，29（1）：1－22.

［16］ MUNKRES J A.Algorithms for Assignment and Transportation Problem［J］.Society for Industrial and Applied Mathematics，1957，5（1）：32－38.

［17］ OSTU N.Threshold Selection Method from Gray－scale Histogram［J］.IEEE Transactions on System，Man，Cybernet，1979，9（1）：62－66.