大数据量遥感分类图像的动态矢量化算法
荣岳成
北京华迪宏图信息技术有限公司,北京100195
1 引 言
遥感数据是GIS重要的信息源[1],遥感数据专题信息也需要进行矢量化表达[2],栅格转矢量是遥感和GIS一体化集成的一项关键技术。近年来,遥感图像的空间分辨逐渐提高,矢量化对计算量和存储的要求也成倍地增长[3],因此,研究适应大数据量遥感图像的高效矢量化算法具有非常重要的价值。
栅格转矢量是GIS研究中的经典课题,积累了比较多的方法。如边缘跟踪法、散列线段聚合法[4]、有向边界法[5]、基于栅格技术的矢量化方法[6]、基于拓扑原理的转换方法[2,7]、基于游程编码的追踪方法[8,9]、双臂链边界跟踪法[10]等。此外,学者们还从拓扑信息自动生成[11]、基于弧-弧的拓扑关系判断[12]等方面对多边形拓扑关系构建算法进行了研究。
传统的矢量化算法在大数据遥感图像矢量化处理中,当图像规模大且内容复杂时,内存可能无法储存所有的边界点或者需要频繁地与外存进行交互,构建多边形时,弧段跟踪耗时较多,拓扑关系判断复杂度高,时间和空间效率低。
与传统矢量化算法不同,本文从顶点提取与图斑矢量化同时进行即动态矢量化的角度,来进行栅格转换矢量根据本文提出的方法,在图斑顶点提取的过程中,检测到能构成封闭多边形的图斑立即将其矢量化,并释放其所占内存,图斑矢量化时,直接将顶点构建成多边形,无须生成中间弧段,并即时形成拓扑关系。
2 矢量化基本概念
遥感中,栅格数据的每个像元(pixel)都表示一定的面积大小,它并不是数学意义上的点,因此,栅格数据矢量化后的矢量数据只有面状(图斑)信息,没有点和线[6]。
在遥感栅格影像矢量化中,有如下约定和定义[2,6]:
定义1 栅格数据矢量化时,只有图斑信息。
定义2 栅格数据中的每个像元都是有大小的,栅格数据矢量化时,最小图斑是一个像元。
定义3 弧段是图斑与图斑之间的连续的边界分界线,弧段内部的点称为坐标点,弧段的端点称为结点。
定义4 坐标点只有两个方向存在边界,而对结点,至少在3个方向上存在边界(如图1)。
定义5 每个矢量多边形由一个外环和多个内环组成(或没有内环),没有内环的多边形称为简单多边形,含有内环的多边形称为复杂多边形。

图1 坐标点(a)~(e)和结点(f)~(k)Fig.1 Nodes(a)~(e)and coordinate points(f)~(k)
3 动态矢量化算法
矢量化算法主要分为3部分:①统计图像各图斑顶点个数;②提取图斑顶点,并判断各图斑顶点,集合能否构成封闭多边形;③将能构成封闭多边形的图斑顶点集合矢量化。在矢量化过程中②和③可以同时进行,并且③执行后,会释放其所占内存,因此,本文算法的矢量化过程是动态的。
3.1 图斑顶点统计
图1中(a)~(e)属于坐标点,(f)~(k)属于结点,只有坐标点或结点能构成图斑边界。其中图1中的第a种坐标点属于冗余坐标点,处理中可以剔除该类型坐标点。在本文中,坐标点和结点统称顶点。栅格图像中的一个图斑是一个四连通区域,每个图斑矢量化后,都对应一个简单多边形或一个复杂多边形,对分类图像中的图斑进行编号,每个图斑将有唯一的编号。
每个环是由一系列首尾重合的顶点构成的封闭多边形。简单多边形对应图斑的顶点个数为外环的顶点个数;复杂多变形对应的图斑的顶点个数为外环与所有内环的顶点个数之和。在图2中,图斑A与C对应简单多边形,顶点个数均为4,图斑B对应复杂多边形,顶点个数为10。
每个顶点的类型,由相邻的4个像元决定,因此在对图像进行扫描时,不需要将整幅图像读入内存,处理一行数据只需将相邻两行读入内存,依次判断每个顶点类型,并将相应的图斑顶点个数计数器更新,处理完之后,下移一行。

图2 图斑顶点个数统计Fig.2 Statistics of vertices in polygon
3.2 图斑顶点提取
图斑顶点提取的流程与图斑顶点个数统计的流程类似,每次读入两行栅格数据到内存,从左至右逐点进行处理,处理中,需要记录每个顶点与其周围4个像元的邻接关系。
对于每个顶点,本文采用如下的结构体表示其信息[2]。

其中,x、y为该点的行列坐标;类型type=2,3,…,11,对应于上面的结点和坐标点情况,表明该矢量点的类型;adj[4]分别记录该点0、1、2、3这4个方向上(依次对应为右、上、左、下)的连接信息。
在顶点提取的过程中,每个图斑的顶点用一个动态容器来存储,顶点提取算法如下:
(1)从图像中取出一个未处理的点,判断该点的类型,如果是顶点,执行(2),否则继续执行(1);
(2)记录该点的x与y方向坐标及点类型,如果adj[4]某方向上有边界,则将其对应元素置为1,否则置为-1,根据顶点周围相邻4个像元的对应的图斑编号,将该顶点插入到包含该点的图斑的多边形顶点容器中;
(3)检测新插入顶点的图斑多边形顶点容器当前顶点数是否等于图斑实际的顶点数,如果相等,则将该图斑多边形顶点容器(集合)进行矢量化,并释放其所占内存;
(4)判断所有点是否都已经被处理完成,如果是,则算法结束,否则继续执行(1)。
从上述算法可以看出,在顶点提取的过程中,完成了图斑矢量化,并且内存中只驻留了已经被扫描且尚未完成扫描的图斑顶点,已经完成扫描和未开始扫描的图斑顶点不会被存储,这样大大降低了存储顶点的内存消耗,有利于提高算法的空间效率。
3.3 图斑顶点矢量化
图斑顶点矢量化首先进行封闭弧段跟踪,然后对封闭弧段进行拓扑关系判断。在封闭弧段跟踪开始前,先通过对图斑顶点容器内所有顶点进行一次扫描,在adj[4]中记录每个顶点上、下、左、右4个方向上与其他顶点的连接信息[2]。封闭弧段的跟踪可以从任意一个顶点开始,其跟踪算法如下:
从图斑顶点容器中选择一个未被跟踪过的顶点,对该顶点按0、1、2、3方向进行遍历,找出第一个具有连接点的方向,不妨设此方向为k,adj[k]中的数值就是下一个顶点的序号,根据跟踪到的该顶点的连接信息进而可以跟踪得到另一个新的顶点,如此下去,直到回到初始出发顶点为止,形成一个封闭多边形。一个封闭多边形跟踪完毕后,应该将其上所有顶点的跟踪标志设置为已跟踪标志,防止被重复跟踪。一个图斑一般会包含若干个封闭多边形,因此,上述跟踪步骤应重复进行,直到所有顶点都已被跟踪过为止。
本文算法的多边形拓扑关系判断简单高效,能以线性时间复杂度完成。由于每个图斑顶点容器中的顶点都属于同一个图斑,因此矢量化后的封闭多边形也必然属于同一个矢量多边形,这样拓扑关系判断只需找出最外层的封闭多边形,其余封闭多边形均会被该多边形包含。最外层多边形的搜索算法如下:比较每个封闭多边形最小外接矩形左上角顶点x方向坐标值,最小坐标值对应的那个封闭多边形即为最外层多边形。
由于最小外接矩形可以在封闭弧段跟踪过程中计算得出,因此,矢量多边形拓扑关系判断以线性时间复杂度完成。
4 动态矢量化算法分析
为了便于后面的讨论,先对符号进行约定。设N和M分别为分类图像的高与宽;矢量化文件共有K个顶点:v1,v2,…,vK,顶点集合V={v1,v2,…,vK};矢量文件共有n个封闭弧段,每个封闭弧段对应的顶点个数分别为:k1,k2,…,kn;矢量化文件共有m个拓扑多边形:s1,s2,…,sm组成,拓扑多边形集合S={s1,s2,…,sm};ysmin与ysmax分别表示多边形s所有顶点中垂直方向坐标的最小值与最大值;xv与yv分别表示顶点v在图像水平与垂直方向的坐标。
4.1 时间复杂度
与传统的矢量化算法相似,动态矢量化算法需要对图像进行遍历,并且在弧段跟踪时,需要对所有顶点进行一次扫描。图像遍历与弧段跟踪的复杂度分别为O(N×M)与O(K)。
封闭弧段间的拓扑关系判断是矢量化算法中的一个难点。传统的矢量化算法中,每个封闭弧段需要与其余所有封闭弧段进行一次包含关系判断,拓扑关系判断的复杂度为O(n2)[13]。采用文献[14—15]中的索引技术进行优化,理想情况下,复杂度接近O(nlogn),但这些算法实现起来较复杂。
动态矢量化算法在拓扑关系判断阶段,属于同一个复杂多边形的封闭弧段划分在一起,只需找出最外层的封闭弧段,拓扑关系判断算法的复杂度为O(n)。
在实际的矢量化过程中,封闭弧段数量可能达到几十万量级,以线性时间复杂度O(n)完成多边形拓扑关系判断,是动态矢量化算法在时间效率上的显著优势。
4.2 空间复杂度
运用传统的矢量化方法进行矢量化处理时,会在内存中保存所有的顶点,空间复杂度为O(K)。
当动态矢量化算法处理到图像的第t行时,只需要存储图像第1行至第t行区域内尚未完成矢量化的多边形中的部分顶点,上述多边形集合St={s∈S|ysmin≤t≤ysmax},需要存储的顶点集合Vt={v∈V|存在s∈St,使得v∈s且yv≤t},易知Vt⊆V。设表示顶点集合Vt的顶点个数,则,只有当对拓扑多边形集合S中的任意一个多边形都满足ysmax=N时,等号才成立。可见,在一般情况下,动态矢量化算法空间复杂度O(Vmax)<O(K)。
Vmax的实际计算非常复杂,与图像大小及图斑的复杂程度都有关。为了对Vmax进行近似的估计,作如下两个假设:①每个拓扑多边形的顶点个数相等,且最小外接矩形的高相同;②拓扑多边形在图像空间中均匀分布。设每个拓扑多边形最小外接矩形的高都为h,当动态矢量化算法处理到第t行时,只需要存储第t-h行到第t行区域内的多边形顶点,其顶点个数为
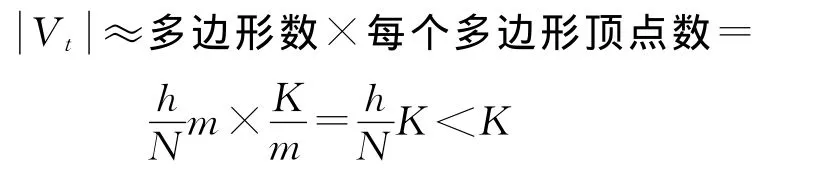
5 试验结果
为了验证本文算法的有效性,在Visual C++环境下开发了相应程序,进行了两组试验。第1组试验与遥感图像处理主流商业软件Arc-GIS10、ENVI4.8以及ERDAS2010的矢量化时间进行了对比,测试的时间包含读入栅格数据与生成矢量文件时间。第2组试验分析了动态化处理对算法运行内存峰值的影响。本文选用不同规模和复杂度的北京一号卫星遥感分类图像,在AMD 2.3GHz CPU,2GB内存的PC上进行矢量化试验,试验结果见图3、图4、表1和表2。
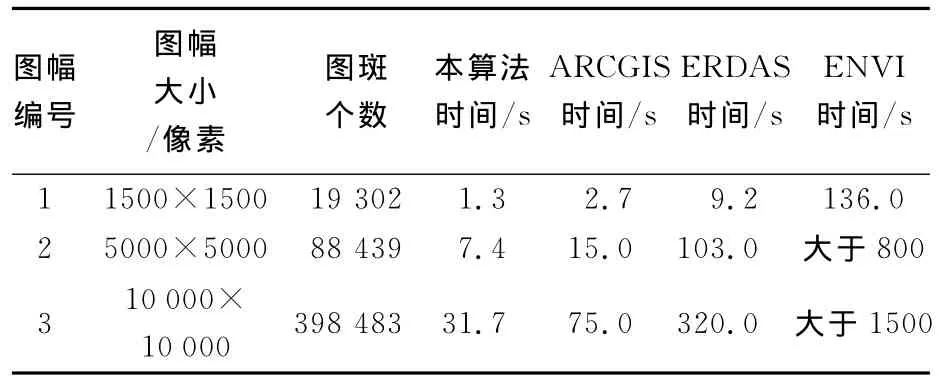
表1 本文算法与ArcGIS、ERDAS以及ENVI矢量化时间的统计Tab.1 The process time of vectorization for different algorithms

表2 动态化处理对算法运行内存峰值的影响Tab.2 The impact of dynamism process on memory peak of vectorization

图3 栅格图像Fig.3 Raster map
图4 矢量结果图Fig.4 Vector map
本文的矢量化结果保持了图斑连通区域边界的原始拓扑结构,矢量化结果无精度损失,如图3与图4所示。采用道格拉斯-扑克算法[18]对边界进行压缩,以提高存储效率,可以作为动态矢量化算法下一步的改进方向。
从表1可以看出,上述商业软件中,ArcGIS矢量化算法效率最高,本文算法是其处理速度的2倍,具有明显优势,并且随着图像规模及图斑数量的增加,优势会更明显,因此,本文算法处理大规模图像具有很高的时间效率。
从表2可以看出,动态矢量化算法所耗内存仅为所有顶点加载到内存进行矢量化处理方法的16%~51%,这是因为进行动态化处理空间复杂度更低,因此,本文算法处理大规模图像具有很高的空间效率。
6 结 论
与传统方法不同,本文算法具有如下特点:
(1)将图斑顶点个数作为判断条件,使图斑顶点的多边形封闭性判断能在常数时间内完成,是本文动态化算法得以高效实现的关键;
(2)在顶点提取过程中将满足封闭性条件的图斑矢量化并动态释放其内存,大大降低了矢量化的内存消耗,保证了空间的高效性;
(3)顶点提取时将各图斑进行分割,各图斑矢量化独立进行直接生成封闭弧段无须产生中间数据,弧段跟踪完成后,能以线性时间复杂度形成拓扑关系,时间效率高;
(4)各图斑矢量化独立进行,非常适合将算法改造成并行化算法,能更充分地发挥多处理器或GPU的计算优势。
本文的矢量化算法已开发为成熟的软件模块,经检验,能快速高效地完成大数据量遥感图像矢量化。
[1] GONG Jianya.An Unified Data Structrue Based on Linear Quadtrees[J].Acta Geodaetica et Cartographica Sinica,1992,21(4):259-266.(龚健雅.GIS中矢量栅格一体化数据结构的研究[J].测绘学报,1992,21(4):259-266.)
[2] CHEN Renxi,ZHAO Zhongming,PAN Jing.A Fast Method of Vectorization for RS Classified Raster Map[J].Journal of Remote Sensing,2006,10(3):326-331.(陈仁喜,赵忠明,潘晶.遥感分类栅格图的快速矢量化方法[J].遥感学报,2006,10(3):326-331.)
[3] JIAO Mingyong,SU Honggen.Improved Algorithms for Raster to Vector and Specific Applications[J].Computer Engineering and Design,2008,29(13):3394-3398.(焦明勇,苏鸿根.栅格转矢量的改进算法及应用[J].计算机工程与设计,2008,29(13):3394-3398.)
[4] HUANG Bo,CHEN Yong.New Approaches for Mutual Transferring of Vector and Raster[J].Remote Sensing Technology and Application,1995,10(3):61-65.(黄波,陈勇.矢量、栅格相互转换的新方法[J].遥感技术与应用,1995,10(3):61-65.)
[5] LI Zhancai,LIU Chunyan.An Efficient Directed Boundary Method for Vectorization of Dot Matrix Image[J].Computer Applications and Software,1997,14(3):48-51.(李占才,刘春燕.点阵图形矢量化的高效方法——有向边界法[J].计算机应用软件,1997,14(3):48-51.)
[6] ZHANG Xiaocan,PAN Yunhe.Vectorization Technique for GIS Grid Data Based on“Grid Technique”[J].Journal of Computer-aided Design & Computer Graphics,2001,13(10):895-900.(章孝灿,潘云鹤.GIS中基于“栅格技术”的栅格数据矢量化技术[J].计算机辅助设计与图形学学报,2001,13(10):895-900.)
[7] SHEN Zhangquan,WANG Renchao.Study on a New Method for Transferring Grid to Vector Using the Topological Theory[J].Journal of Remote Sensing,1999,3(1):38-42.(沈掌泉,王人潮.基于拓扑关系原理的栅格转换矢量方法的研究[J].遥感学报,1999,3(1):38-42.)
[8] WU Huayi,GONG Jianya,LI Deren.Non-boundary Run-Length Encoding System for Raster and Its Relevant Algorithms[J].Acta Geodaetica et Cartographica Sinica,1998,27(1):63-68.(吴华意,龚健雅,李德仁.无边界游程编码及其矢栅直接相互转换算法[J].测绘学报,1998,27(1):63-68.)
[9] XIE Shunping,DU Jinkang,WANG Lachun,et al.Approach of Vectorization for GIS Raster Data Based on Runlength Encoding System [J].Acta Geodaetica et Cartographica Sinica,2004,33(4):323-327.(谢顺平,都金康,王腊春,等.基于游程编码的GIS栅格数据矢量化方法[J].测绘学报,2004,33(4):323-327.)
[10] TENG Junhua,WANG Fahui,LIU Yu.An Efficient Algorithm for Raster-to-vector Data Conversion [J].Annals of GIS.2008,14(11):54-62.
[11] CHEN Chun,ZHANG Shuwen,XU Guifen.The Basis for Generation of Topologic Information of Polygons in GIS[J].Acta Geodaetica et Cartographica Sinica,1996,25(4):266-271.(陈春,张树文,徐桂芬.GIS中多边形图拓扑信息生成的数学基础[J].测绘学报,1996,25(4):266-271.)
[12] QI Hua.The Optimization and Improvement for the Algorithm Steps on the Automatic Creation of Topological Relation of Polygons[J].Acta Geodaetica et Cartographica Sinica,1997,26(3):254-260.(齐华.自动建立多边形拓扑关系算法步骤的优化与改进[J].测绘学报,1997,26(3):254-260.)
[13] ZHANG Xingyue,WANG Min,JIANG Sheng.A Novel Approach for Raster Data Vectorization [J]. Geoinformation Science,2008,10(16):730-735.(张星月,汪闽,蒋圣.一种新的栅格数据矢量化方法[J].地球信息科学,2008,10(6):730-735.)
[14] GUTTMAN A.R-trees:A Dynamic Index Structure for Spatial Searching[C]∥ACM SIG-MOD Record.New York:ACM,1984:47-57.
[15] XU Shaoping,WANG Minyan,WANG Weili.A New Index Structure for Moving Object Spatial Database Based on R Tree and Quan Tree[J].Computer & Digital Engineering,2006,34(3):54-57.(徐少平,王命延,王炜立.一种基于R树和四叉树的移动对象空间数据库混合索引结构[J].计算机与数字工程,2006,34(3):54-57.)
[16] WANG Jing,JIANG Gangwu.Researching and Realization of the Quick Compression Method Aimed at the Non-Topology Vector Data [J].Acta Geodaetica et Cartographica Sinica,2003,32(2):173-177.(王净,江刚武.无拓扑矢量数据快速压缩算法的研究与实现[J].测绘学报,2003,32(2):173-177.)

