确定大地水准面的Tikhonov最小二乘配置法
欧阳永忠,邓凯亮,黄谟涛,暴景阳,陆秀平,吴太旗,刘传勇
1.武汉大学 测绘学院,湖北 武汉 430079;2.海军海洋测绘研究所,天津 300061;3.大连舰艇学院 海测工程系,辽宁大连 116018
大地水准面是定义正高高程系统的高程基准面,也是反映地球内部结构和密度分布特征的物理面。确定高精度高分辨率的大地水准面,已成为21世纪大地测量学科发展全局性的战略目标[1-3]。国内外学者就大地水准面的确定做了许多有益的研究,提出了Stokes理论、Molodensky理论、Bjerhammar理论和最小二乘配置理论等[4-6]。其中以统计理论为基础的最小二乘配置理论,由于它具有能对多种类型的重力观测量进行联合处理的特性,在大地水准面确定的应用上受到广泛关注[7-16]。利用最小二乘配置法确定大地水准面的关键是协方差函数的确定[7-9],但是即使拟合的协方差函数能充分表达研究区域范围内重力场特性,由于在大地水准面的确定过程中需要对协方差矩阵进行求逆,而协方差矩阵的求逆过程是信号放大的非平稳过程,协方差矩阵的小奇异值将放大观测误差对配置结果的影响,导致配置结果不稳定且精度偏低[17]。当已知的重力观测量存在观测误差时,最小二乘配置法难以得到稳定精确的大地水准面解。
本文在确定大地水准面的最小二乘配置法中,引入Tikhinov正则化法,对协方差矩阵进行正则化处理,以抑制协方差矩阵的小奇异值对观测误差的放大影响,得到稳定且高精度的大地水准面高。基于EGM2008重力场模型计算了一组重力异常数据,以该重力异常作为基础数据,联合最小二乘配置法和Tikhonov正则化法确定大地水准面,以验证该方法的有效性。
1 最小二乘配置法
1.1 基本原理
重力场的所有重力场观测量都可看成空间平稳随机场的随机量,任意重力场观测量l可表示为

式中,Li为由扰动位T表示重力场观测量l的线性泛函算子;e为观测噪声,其向量形式为

式中,t=LT,是l的信号部分。
最小二乘配置公式[4-5]为
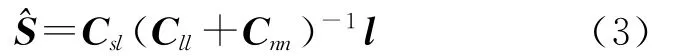
依据式(3),以重力异常Δg作为基础数据,基于最小二乘配置法确定大地水准面的公式为

式中,CNΔg为大地水准面与重力异常的互协方差矩阵;CΔgΔg为重力异常的协方差矩阵;Cnn是观测噪声的协方差阵。
1.2 协方差函数的确定
扰动位T的协方差函数可表示为[7]


依据位理论、边值理论和协方差传播定律,基于移去-恢复思想,重力异常与大地水准面之间协方差函数可写为
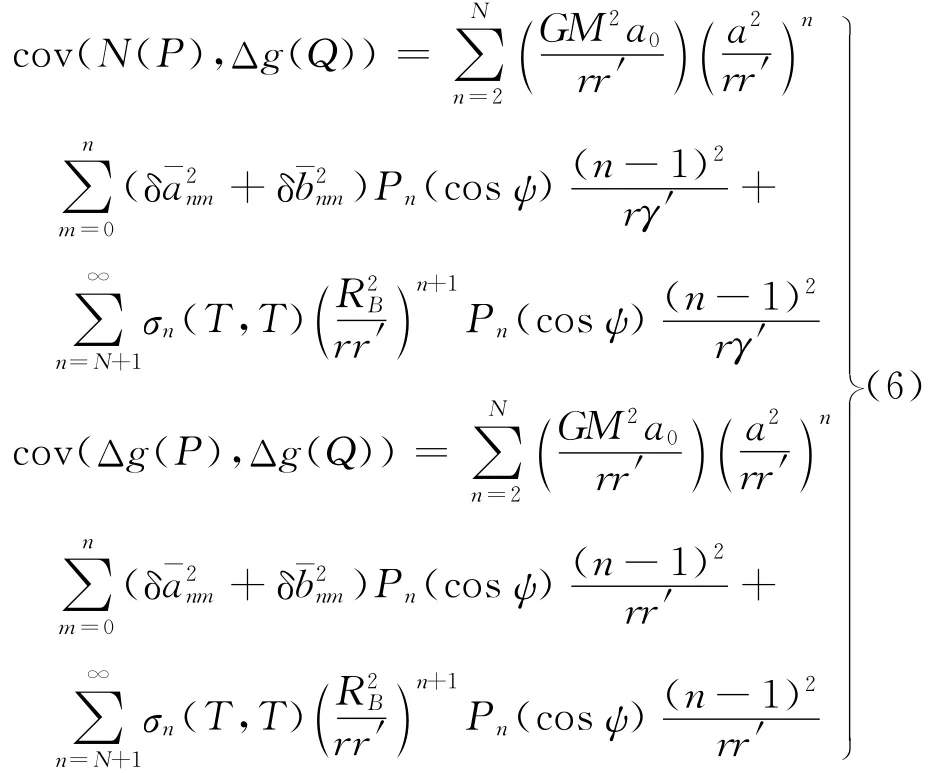

球面重力异常经验协方差C(ψ)的公式[11,18]为
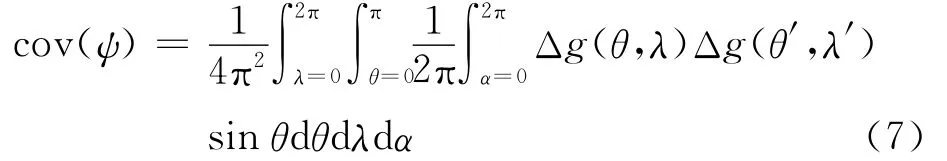
式中,θ为地心余纬;λ为地心经度;α为方位角。若记球面上重力异常的格网值为f,面积为B,则式(7)的离散形式为
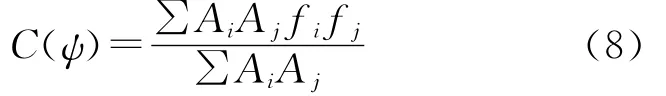
依据重力异常经验协方差C(ψ)拟合式(6)中的第二项,求得常数a0、A和RB,进而确定重力异常和大地水准面之间的互协方差函数。
2 Tikhonov正则化法
依据式(4),在大地水准面的确定过程中需要对协方差矩阵CΔgΔg进行求逆,而协方差矩阵的条件数较大,其求逆过程是信号放大的非平稳过程,小的观测误差往往会引起结果的较大误差,属于不适定问题[17]。正则化算法的实质就是通过选择合适的正则化参数来抑制观测噪声对参数估值的影响,以得到稳定、精确的解。在众多的正则化方法中,以Tikhonov正则化法应用最为广泛[19-21]。
2.1 Tikhonov正则化法
Tikhonov正则化法的实质是用相邻的适定解去逼近源问题的解[22]。取观测值Δg的个数为q,令

则,x是一个q向量,式(4)可写为
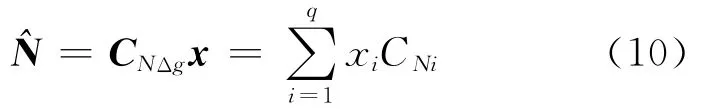
由式(10)可看出,是q个CNi的线性组合,由于CNi可由协方差函数计算得到,故只要得到稳定精确的x,就能确定稳定精确的。
将式(9)写为
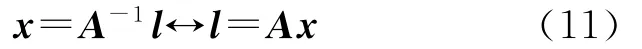
式中,A=CΔgΔg+Cnn,l=Δg
则式(11)的正则化函数为
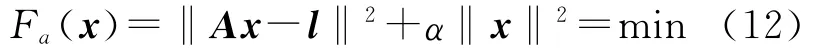
式中,α>0是正则化参数;‖x‖表示x的范数。
根据式(12)的约束条件,可得Tikhonov正则化解
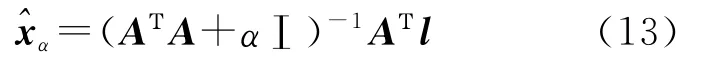
在正则化解的两边乘以CNΔg,则得到

所以求得稳定精确的大地水准面高的关键是得到稳定精确的
式(11)在频域内的形式为
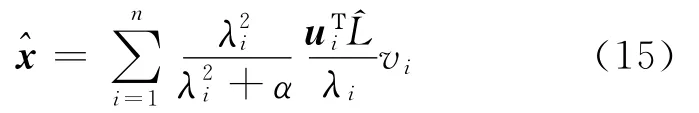
为了分析正则化参数的影响,引入均方误差MSE
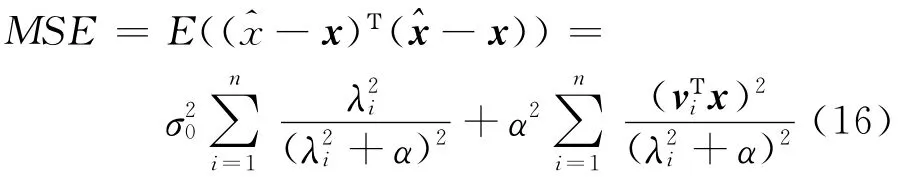
由式(16)可知,Tikhonov正则化法的估值误差包括两部分:前者是测量误差引起的估值误差,随着正则化参数α的增大而减小;后者是正则化引起的估值误差,随着正则化参数α的增大而增大。如何选择正则化参数α是整个正则化算法的关键。
2.2 正则化参数的选取
近年来,统计学界和大地测量学界提出了多种方法选择正则化参数,比如L曲线法[19-20]和广义交互确认法(generalized cross-validation,GCV)[21-26]等。这里选择GCV法选择正则化参数。
该函数定义为
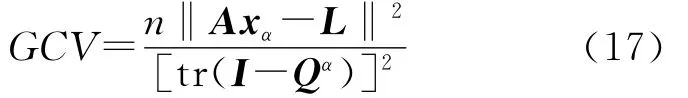
式中,Qα是所谓的影响矩阵,由Axα=QαL定义;n为观测值个数;tr为矩阵的迹。
最佳的正则化参数α对应于GCV函数的最小值。
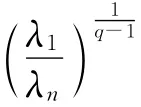

本文的试验取q为100[19],以选取的正则化参数的示意图见图1。
3 仿真试验及精度分析
为了验证联合最小二乘配置法和Tikhonov正则化法确定大地水准面的有效性,设计了以重力异常作为基础数据确定大地水准面的仿真试验。
3.1 数据准备
基于EGM2008重力场模型计算的重力异常作为仿真试验的基础数据。EGM2008重力场模型[27]是由 NGA(National Geospatial-intelligence Agency)释放的全球超高阶地球重力场模型,由卫星重力测量、卫星测高和地面重力观测等资料联合解算得到,模型阶数达到2160。EGM2008重力场模型导出的重力异常在我国大陆的总体精度为10.5mGal(1mGal=10-5m/s2)[28]。
基于EGM2008重力场模型分别计算山区、丘陵和海域2160的重力异常Δg山、Δg丘和Δg海(见图1),大地水准面高N山、N丘和N海(见图2)。区域范围都为1°×1°,格网间距都为2′×2′。考虑移去-恢复技术的应用,取EGM2008重力场模型的360阶作为参考模型,得到参考重力异常Δg′山、Δg′丘和 Δg′海和参考大地水准面高N′山、N′丘和N′海。重力异常和大地水准面的统计特性见表1和表2。
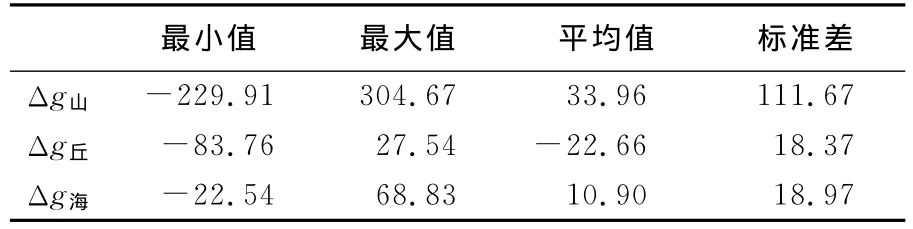
表1 仿真区域重力异常特性的统计Tab.1 Characteristics of gravity anomalies at simulation area mGal

表2 仿真区域大地水准面特性的统计Tab.2 Characteristics of Geoids at simulation area mGal
3.2 试验步骤
为了模拟重力异常的观测误差,在仿真的重力异常Δg山、Δg丘和Δg海引入3种观测误差分别是零均值的白噪声:e1(σ=±1mGal)、e2(σ=±3mGal)、e3(σ=±5mGal)。以山区重力异常为例,试验步骤如下:
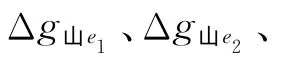
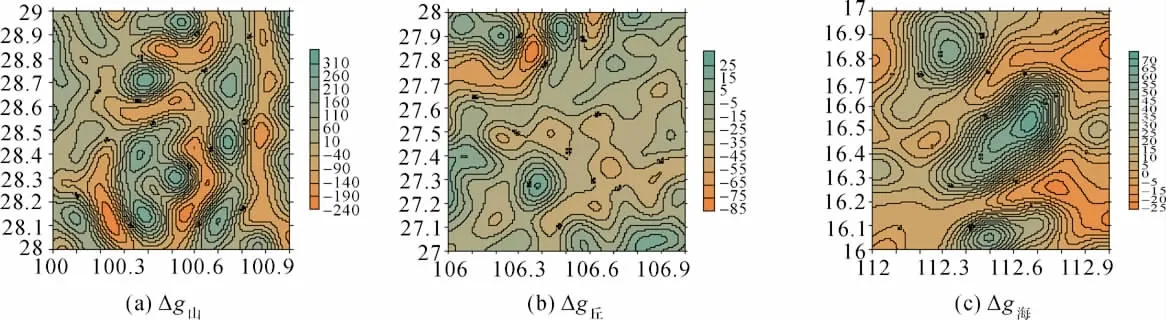
图1 仿真的重力异常Fig.1 Simulative gravity anomalies
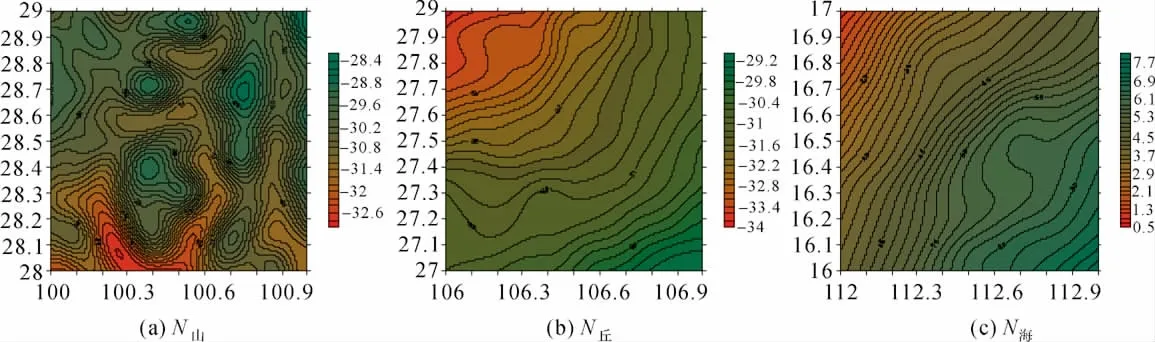
图2 仿真的大地水准面Fig.2 Simulative geoids
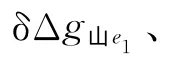

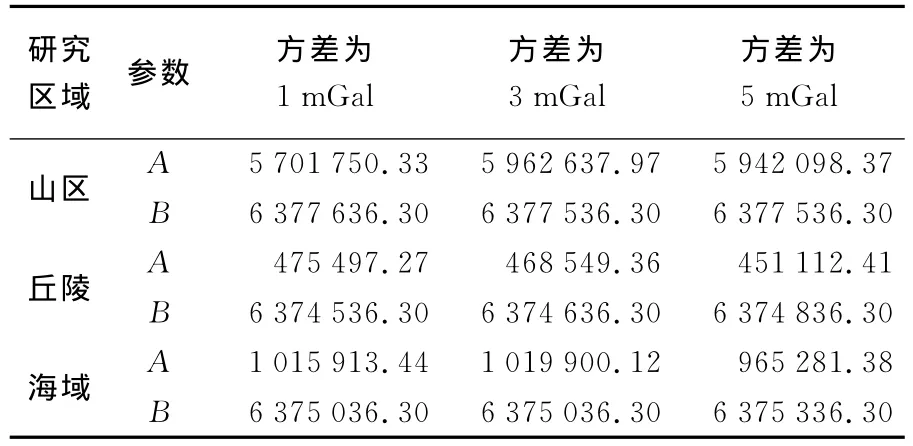
表3 各误差条件下协方差函数的参数Tab.3 Parameters of the covariance function in three kinds of errors
(4)在已知协方差函数的系数A和RB的基础上,依据式(6)中计算重力异常与大地水准面的协方差矩阵CNΔg和阶方差矩阵CΔgΔg。
(5)依据Tikhonov正则化原理,利用GCV法计算阶方差矩阵CΔgΔg求逆时的正则化参数(见图3)。
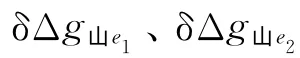
丘陵区域和海洋区域的仿真试验和山区区域的仿真试验类似。
3.3 结果比较和分析
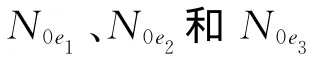
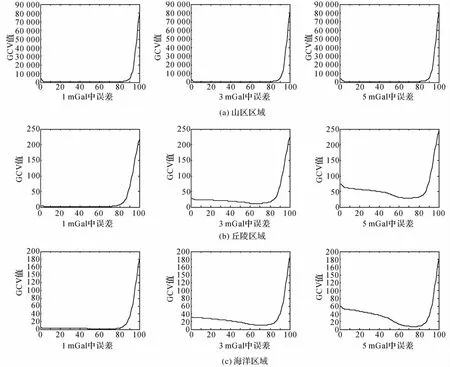
图3 各误差条件下协方差矩阵CΔgΔg用GCV法确定正则化参数示意图Fig.3 Regularization parameters chosen by the GCV method in three kinds of errors
为了验证本方法的效果,设计了3种计算方法。
方法1:Stokes法(积分半径取1度);
方法2:直接的最小二乘配置法;
方法3:联合最小二乘配置法和Tikhonov正则化法的算法。
比较结果见表4。
由表4可以看出:
(1)在设计的3种误差条件下,方法2计算的大地水准面出现千米级误差,表明选择取全区域观测值拟合协方差系数将增大协方差矩阵之间的相关性,使得矩阵严重病态。
(2)在设计的3种误差条件下,方法3计算的大地水准面的标准差,在山区区域分别为9.19cm、9.14cm和8.98cm;在丘陵区域分别为3.69cm、3.80cm和3.36cm;在海洋区域分别为2.14cm、1.98cm和1.96cm,远优于方法2计算的大地水准面,表明方法3能有效抑制观测误差对结果的影响,得到稳定精确的大地水准面高。
(3)方法1计算的大地水准面的标准差,在山区区域分别为15.01cm、15.06cm和15.09cm;在丘陵区域分别为5.36cm、5.51cm和5.51cm;在海洋区域分别为2.93cm、3.14cm和3.19cm,与方法3比较,二者精度相当。
(4)在误差增大的情况下,方法3的正则化参数显著增大,在山区区域分别为495.50、10 796.80和41 125.74;在丘陵区域分别为90.54、953.37和2 577.74;在海洋区域分别为1 867.72、7 219.84和38 015.51。对应的CΔgΔg条件数依次减小,在山区区域分别为8 724.81、1 922.93和981.87;在丘陵区域分别为981.87、302.84和182.93;在海洋区域分别为302.84、154.63和66.75,同时大地水准面的标准差也相应减小,表明正则化参数严重影响方法3的稳定性和精度。

表4 与大地水准面N0的比较Tab.4 Comparison Results of Geoids Differences between calculated results and Simulative Geoid N0 cm
4 结束语
最小二乘配置法由于能融合不同种类重力观测数据确定大地水准面的特性而受到广泛关注。但由于协方差矩阵存在病态性,微小的观测误差将被观测数据协方差矩阵的小奇异值放大,导致计算的配置结果不稳定且精确偏低。
在最小二乘配置法中引入Tikhonov正则化法,利用正则化参数修正协方差矩阵的小奇异值,能抑制其对观测误差的放大影响。基于Tikhonov-LSC法计算大地水准面,能有效提高稳定性和精度。通过以EGM2008重力场模型分别计算的山区、丘陵和海域重力异常作为基础数据确定相应区域大地水准面的试验,验证了该方法的有效性。
Tikhonov正则化法能有效改进基于重力异常利用最小二乘配置理论计算大地水准面的精度和稳定性。但Tikhonov正则化法是否适用于最小二乘配置理论的最优正则化法,还有待进一步研究。
[1] CHAO Dingbo,SHEN Wenbin,WANG Zhengtao.Investigation of the Possibility and Method of Determining Global Centimeter-level Geoid[J].Acta Geodaetica et Cartographica Sinica,2007,36(4):370-376.(晁定波,申文斌,王正涛.确定全球厘米级大地水准面的可能性与方法探讨[J].测绘学报,2007,36(4):370-376.)
[2] XU Xi,ZHU Jianjun.Relative Accuracy Estimation for Determining Regional Gravimetric Geoid[J].Acta Geodaetica et Cartographica Sinica,2009,38(5):383-390.(许曦,朱建军.区域重力大地水准面确定的相对精度估计[J].测绘学报,2009,38(5):383-390.)
[3] LIU Zhenyu,GAO Binghao.Establishing the West Jilin Quasi-geoid Based on CQG2000[J].Acta Geodaetica et Cartographica Sinica,2010,39(5):441-443.(刘振宇,高炳浩.基于CQG2000的吉林省西部地区似大地水准面的建立[J].测绘学报,2010,39(5):441-443.)
[4] MORITZ H.Advanced Physical Geodesy[M].Karlsruhe:Wichmann,1980.
[5] HEISKANEN W A,MORITZ H.Physical Geodesy[M].San Francisco:Freeman and Company,1967.
[6] BJERHAMMAR A.A New Theory of Geodetic Gravity[R].Stockholm:Freeman and Company,1967.
[7] WU Xing,ZHANG Chuanding,LIU Xiaogang.Least-squares Collocation Harmonic Analysis of the Radial Satellite Gravity Gradients[J].Acta Geodaetica et Cartographica Sinica,2010,39(5):471-477.(吴星,张传定,刘晓刚.卫星重力径向梯度数据的最小二乘配置调和分析[J].测绘学报,2010,39(5):471-477.)
[8] CHAI Hongzhou,CUI Yue,MING Feng.The Determination of Chinese Mainland Crustal Movement Model Using Leastsquares Collocation[J].Acta Geodaetica et Cartographica Sinica,2009,38(1):61-65.(柴洪洲,崔岳,明锋.最小二乘配置方法确定中国大陆主要块体运动模型[J].测绘学报,2009,38(1):61-65.)
[9] ZHANG Chuanyin,DING Jian,CHAO Dingbo.General Expression of Least Squares Collocation in Gravity Field[J].Geomatics and Information Science of Wuhan University,2007,32(5):431-434.(章传银,丁剑,晁定波.重力场最小二乘配置通用表示技术[J].武汉大学学报:信息科学版,2007,32(5):431-434.)
[10] ZOU Xiancai,LI Jiancheng.A Geoid Determination Using Least-Squares Collocation[J].Geomatics and Information Science of Wuhan University,2004,29(3):218-222.(邹贤才,李建成.最小二乘配置方法确定大地水准面的研究[J].武汉大学学报:信息科学版,2004,29(3):218-222.)
[11] TSCHERNING C C,RAPP R H.Closed Covariance Expressions for Gravity Anomalies,Geoid Undulations and Deflections of the Vertical Implied by Anomaly Degree Variance Model[R].Ohio:Ohio State University,1974.
[12] KNUDSEN P.Estimation and Modelling of the Local Empirical Covariance Function Using Gravity and Satellite Altimeter Data[J].Bulletin Geodesique,1987,61:145-160.
[13] WEN Hanjiang.The Estimation of Covariance Function in Least Squares Collocation[J].Science of Surveying and Mapping,2000,25(3):37-40.(文汉江.最小二乘配置法中协方差函数的计算[J].测绘科学,2000,25(3):37-40.)
[14] AYHAN M E.Geoid Determination in Turkey (TG-91)[J].Journal of Geodesy,1993,67(1):10-22.
[15] ARABELOS D N,TSCHERNING C C.Error-Covariance of the Estimates of Spherical Harmonic Coefficients Computed by LSC,Using Second-order Radial Derivative Functional Associated with Realistic GOCE Orbits[J].Journal of Geodesy,2009,83(5):419-430.
[16] KOTSAKIS C.Least-Squares Collocation with Covariancematching Constraints[J].Journal of Geodesy,2007,81(10):661-677.
[17] DENG Kailiang.Research on the Procession,Combination and Application of the Muti-source Gravity Data on the Sea[D].Dalian:Dalian Naval Academy,2011.(邓凯亮.海域多源重力数据的处理、融合及应用研究[D].大连:大连舰艇学院,2011.)
[18] LU Zhonglian.Theory and Method of Earth’s Gravity Field[M].Beijing:PLA Publishing House,1996.(陆仲连.地球重力场的理论与方法[M].北京:解放军出版社,1996.)
[19] WANG Zhenjie.Research on the Regularization Solutions of Ill-posed Problems in Geodesy[D].Wuhan:Institute of Geodesy and Geophysics Chinese Academy of Sciences,2003.(王振杰.大地测量中不适定问题的正则化解法研究[D].武汉:中国科学院测量与地球物理研究所,2003.)
[20] DENG Kailiang,BAO Jingyang,HUANG Motao,et al.Simulation of Tikhonov Regulation Algorithm in Downward Continuation of Airborne Gravity Data[J].Geomatics and Information Science of Wuhan University,2010,35(12):1414-1417.(邓凯亮,暴景阳,黄谟涛,等.航空重力数据向下延拓的Tikhonov正则化法仿真研究[J].武汉大学学报:信息科学版,2010,35(12):1414-1417.)
[21] SHEN Yunzhong,XU Houze.Spectral Decomposition Formula of Regularization Solution for Ill-Posed Equation[J].Journal of Geodesy and Geodynamics,2002,33(3):11-14.(沈云中,许厚泽.不适定方程正则化算法的谱分解式[J].大地测量学与地球动力学,2002,33(3):11-14.)
[22] GOLUB G H,MATT U V.Generalized Cross-validation for Large-scale Problems [J].Journal of Computational and Graphical Statistics,1997,6(1):1-34.
[23] LIU Jijun.Regularization Method and Application of the Ill-posed Equation[M].Beijing:Science Press,2005.(刘继军.不适定问题的正则化方法及应用[M].北京:科学出版社,2005.)
[24] KUSCHE J,KLEES R.Regularization of Gravity Field Estimation from Gravity Gradients[J].Journal of Geodesy,2002,76(10):359-368.
[25] PAVLIS N K,HOLMES S A,KENYON S C,et al.An Earth Gravitational Model to Degree 2160:EGM2008[C]∥Proceedings of the 2008General Assembly of the European Geosciences Union,Vienna:[s.n.],2008.
[26] ZHANG Chuanying,GUO Chunxi,CHEN Junyong,et al.EGM2008and Its Application Analysis in Chinese Mainland[J].Acta Geodaetica et Cartographica Sinica,2009,38(4):283-289.(章传银,郭春喜,陈俊勇,等.EGM2008地球重力场模型在中国大陆适用性分析[J].测绘学报,2009,38(4):283-289.)

