Clifford代数Clp,q(p+q=3)的矩阵表示

张桂颖,李武明

(通化师范学院 数学学院,吉林 通化 134002)

Clifford代数[1-3]Clp,q(p+q=3)的生成空间是p,q(p+q=3),其基元为

1,e1,e2,e3,e12,e13,e23,e123

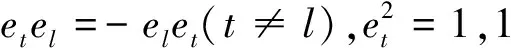
a=a0+a1e1+a2e2+a12e12+a3e3+

a13e13+a23e23+a123e123,

其中系数均为实数.

1 Clp,q(p+q=3)的矩阵表示

定理1Clp,q(p+q=3)可以同构嵌入到Mat(2,) ,映射为

证明 ∀a∈Clp,q(p+q=3) 均有

a=a0+a1e1+a2e2+a12e12+a3e3+
a13e13+a23e23+a123e123=
(a0+a1e1+a2e2+a12e12)+
(b0+b1e1+b2e2+b12e12)e123=
α+βe123,

其中b0=a123,b1=a23或-a23,b2=a13或

-a13,b12=-a3,α,β∈.

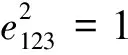
有了这样的一个同构嵌入以后进而我们会发现:

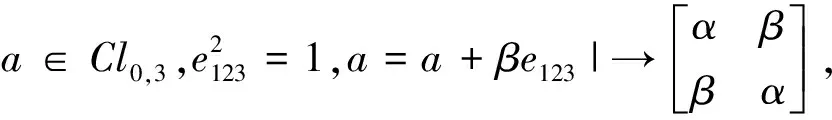
以上我们证明了Clp,q(p+q=3)从生成结构上看都可以表示成2阶矩阵,进而找到其高阶实矩阵表示.下面我们换一种角度,分别找到Cl3,1,Cl2,1,Cl0,3的矩阵表示,然后再给出一个统一表达式.

2 Clp,q(p+q=3)的2阶矩阵表示

命题1Cl3,0的2阶椭圆复矩阵表示为

L(a)=

其中i是椭圆虚单位.

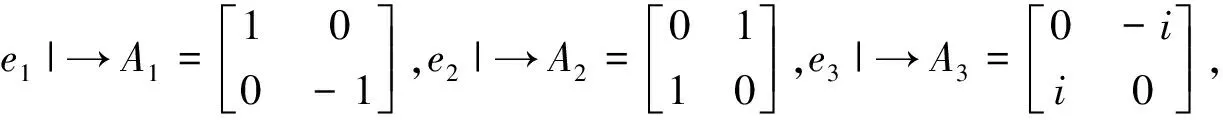
验算有

其中A123=A1A2A3,Atl=AtAl,由此说明

Cl3,0≅.

命题2Cl2,1的2阶双曲复矩阵表示

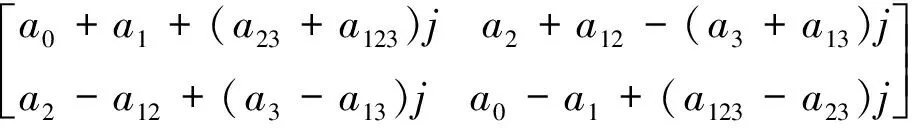
其中j是双曲虚单位.

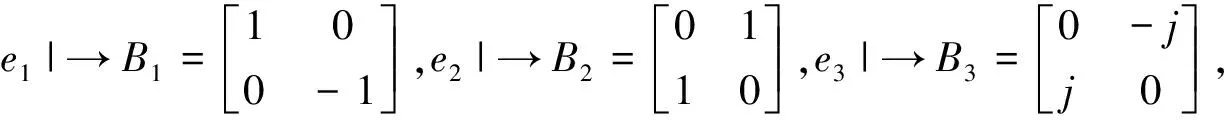
验算有

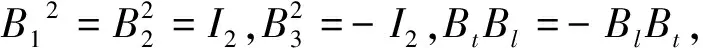
其中B123=B1B2B3,Btl=BtBl,由此说明

Cl2,1≅.

命题3Cl0,3的2阶四元数矩阵表示为

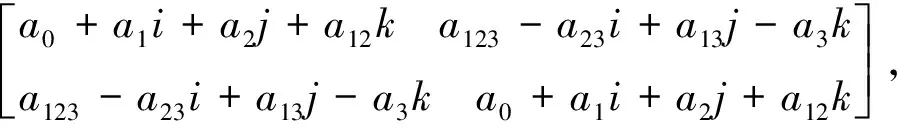
其中i,j,k是四元数虚单位.

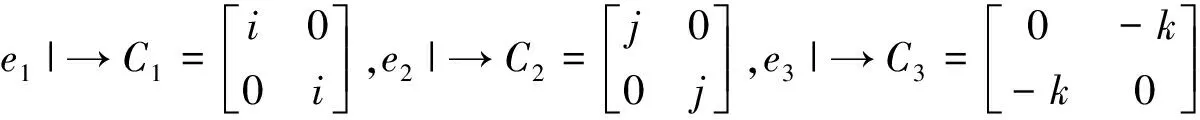
验算有

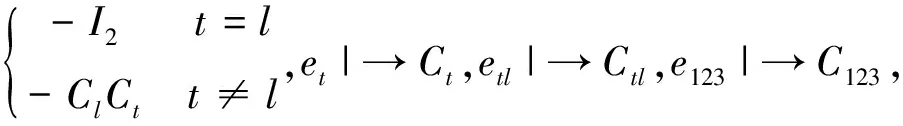
其中C123=C1C2C3,Ctl=CtCl,由此说明

Cl0,3≅.

实际上Cl0,3的这种2阶四元数矩阵表示形式与1中所谈到的形式是一致的,而且Cl0,3的2阶四元数矩阵表示方法有多种形式,比如当取

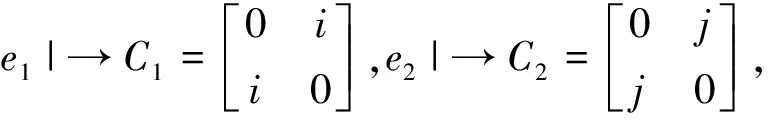
我们可以计算出

验算有Cl0,3≅,进而给出另一种矩阵表示

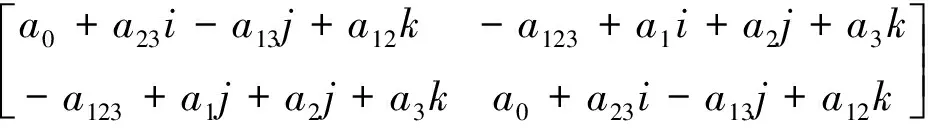
综上我们可以有

定理2Clp,q(p+q=3)可以表示成2阶矩阵,其中Cl3,0,Cl2,1,Cl0,3分别可以表示成2阶的椭圆复矩阵、双曲复矩阵、四元数矩阵.

参考文献：

[1]Lounesto P.Clifford algebra and spinord[M].New York:Cambridge University Press,2001.

[2]李武明.Clifford代数与Minkowski空间的性质[J].吉林大学自然科学学报,2000,13(40).

[3]李武明,张庆成.四维双曲复空间与Lorentz群[J].东北师大学报:自然科学版,2005,37(2).

[4]张桂颖,纪云龙,李武明.Clifford代数Clp,q的幂等元[J].长春工业大学学报:自然科学版,2012,33(4).

[5]李武明.Pauli矩阵的若干性质及应用[J].通化师范学院学报,2003,24(6).

[6]张桂颖,李武明.Clifford代数Cl2,1的若干性质[J].通化师范学院学报,2012,33(2).