半平面上有限级Laplace-Stieltjes变换的正规增长

兰丽英

(江西理工大学应用科学学院，江西赣州341000)

半平面上有限级Laplace-Stieltjes变换的正规增长

兰丽英

(江西理工大学应用科学学院，江西赣州341000)

研究了在一般的指数条件下，右半平面上有限级Laplace-Stieltjes变换的正规增长性与它的系数的关系，得到了一个充要条件．

Laplace-Stieltjes变换；型函数；增长级；精确级

0 引言

考虑由Laplace-Stieltjes变换所定义的函数

式（1）中：a（x）是对于x≥0有定义的实数或复数值函数，而且它在任何闭区间[0,X]（0＜X＜+∞）上是囿变的.记

作序列

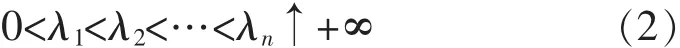
由文献[1]知当序列（2）满足

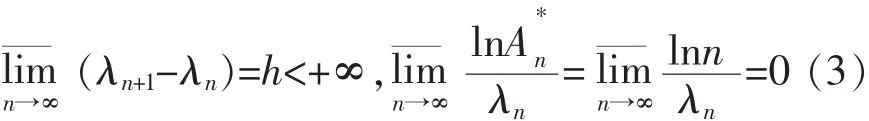
时，式（1）定义了一个右半平面的解析函数.

定义1F（s）在右半平面Re s＞0的增长级ρ定义为

定义2设式（1）的级ρ为有限正数，仿照文献[2]，引进U（r）=rρ（r）.其中ρ（r）在r＞r0上非负，连续，单调.且满足

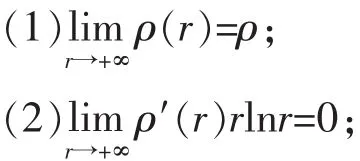
（3）对每个正数k有U（kr）=[kρ+o（1）]U（r）（r→+∞），并且当r＞r0′＞r0时，U（r）为r的增函数.若称F（s）在Re s＞0上具有F（s）在Re s＞0上的精确级，称F（s）的型函数.

当ρ=0，0＜ρ＜+∞或ρ=+∞时，式（1）分别称为零级，有限级和无限级Laplace-Stieltjes变换.关于有限级Laplace-Stieltjes变换，在文献[3]中有如下结果.

定理1设有限ρ级Laplace-Stieltjes变换式（1）满足式（3）和

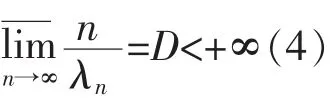
则

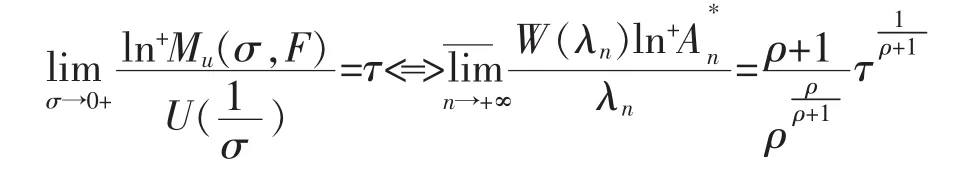
并且存在一个递增正整数列｛nv｝，使

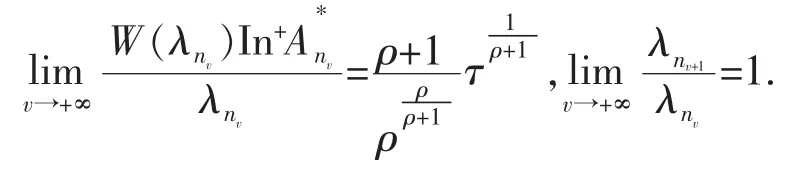
其中0＜τ＜+∞，U（r）为定义2中的型函数，r=W（t）是t=rU（r）的反函数.

文中将在更一般的指数条件下讨论有限级Laplace-Stieltjes变换的精确级与系数的关系，所得结果简化并推广了上述结果.在文中，C表示常数，但前后数值可能不同.

1 引理

引理1[4-5]设b＞0，σ＞0，则函数

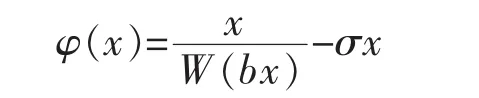
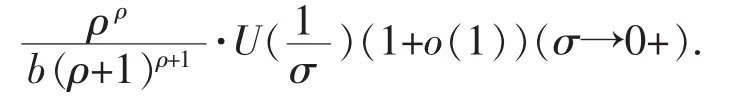
引理2[4-6]设a＞0，λ＞0，则函数

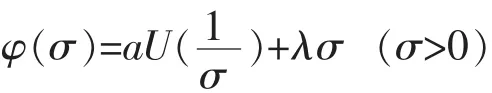
其中r=W（t）与t=rU（r）互为反函数，且

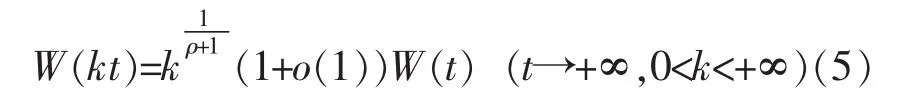
引理3[4-7]设U（r）为定义2中的型函数，A＞0，{λnv}为一列严格递增正数列，存在一列单调递减收敛于零的正数列{σv}，使

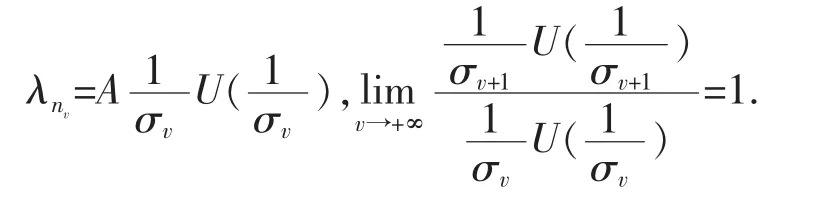
引理4[8]设有限ρ级Laplace-Stieltjes变换式（1）满足式（3）和

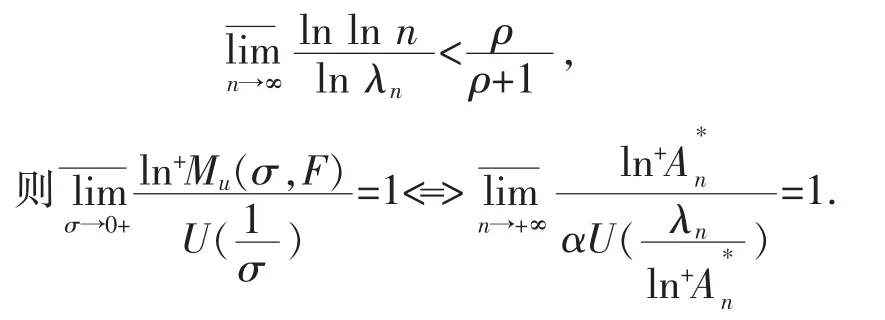
其中α=（ρ+1）ρ+1·ρ-ρ，U（r）为定义2中的型函数.

2 主要结果

定理2设有限ρ级Laplace-Stieltjes变换式（1）满足式（3）和

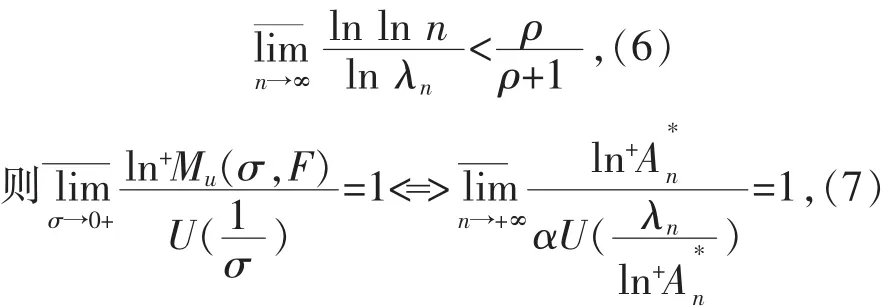
并且存在一个递增正整数列{nv}，使

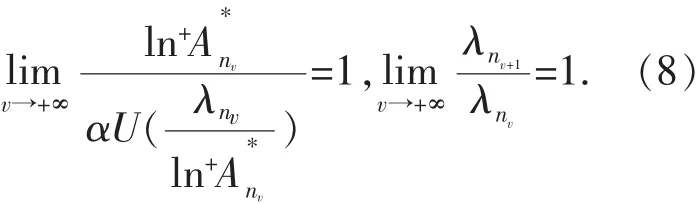
其中α=（ρ+1）ρ+1·ρ-ρ，U（r）为定义2中的型函数.

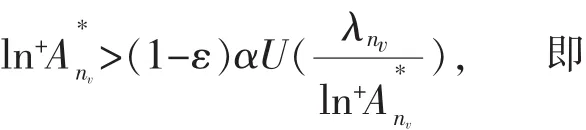
由于r=W（t）与t=rU（r）互为反函数，且它们都是单调递增，所以

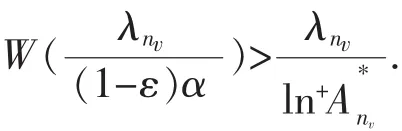
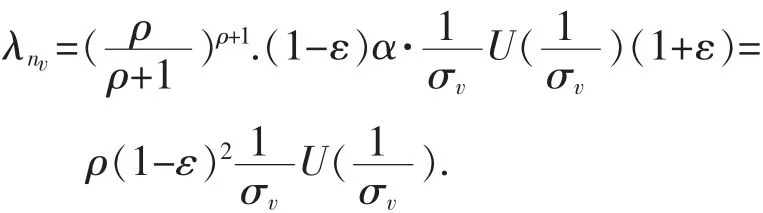
则由引理3得σv↓0.于是，对任意充分小的σ＞0，v∈N+，使σv+1＜σ＜σv，所以由引理1和引理3

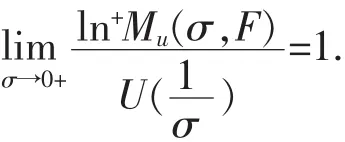
“必要性”若式（7）左边成立，由引理4知，式（7）右边也成立.下面证明式（8）成立.取单调下降正数列{εk}→0，令

由式（7）右边知，对每个k∈N+，Ek为非空无限集且Ek+1Ek.将Ek中正整数从小到大排列，面分两种情况讨论：

（1）若对每个k∈N+，

注意到Ek+1Ek，可取Nk+1＞Nk，因此Ek的子集

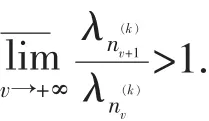
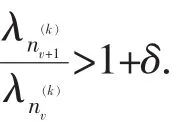
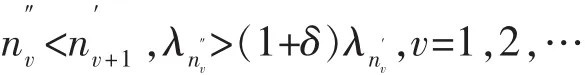
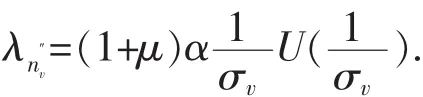
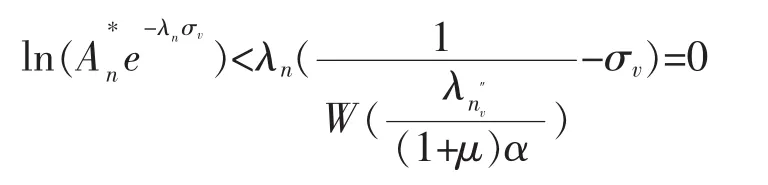
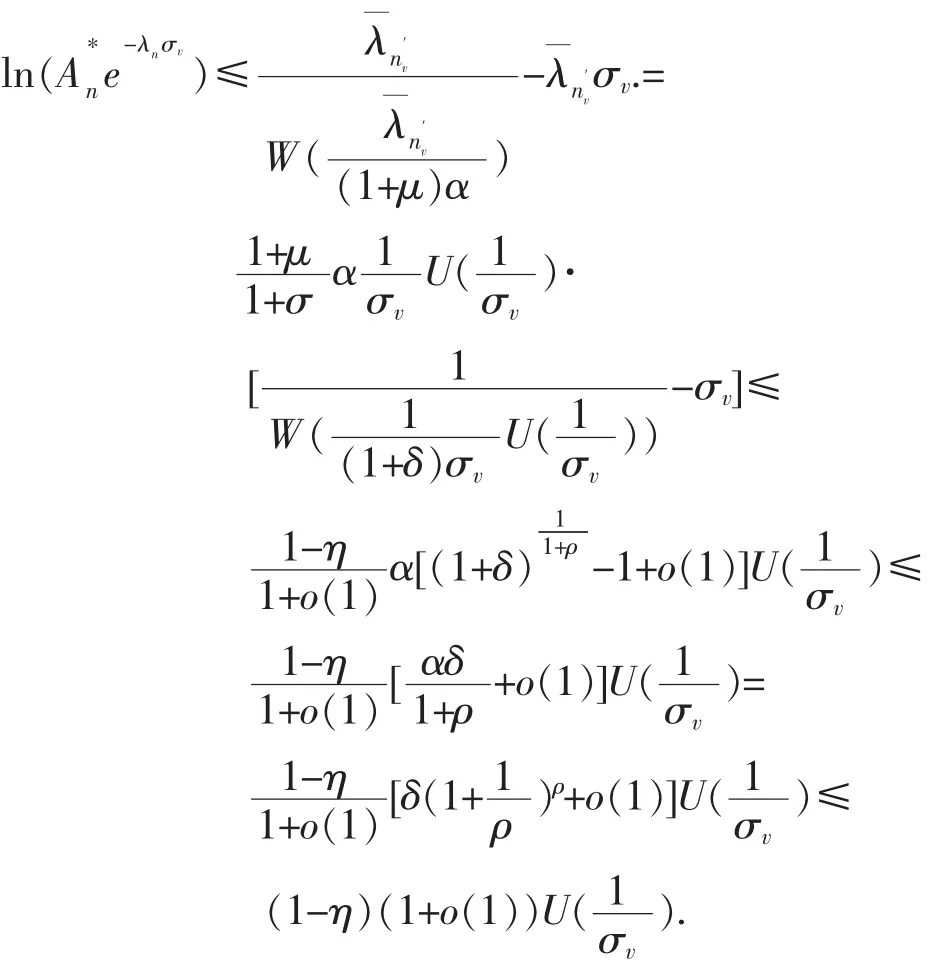
故当n≥n0时，

则对任意t∈R，有

所以当λn＜x≤λn+1，σv＞0时

利用式（6），可得

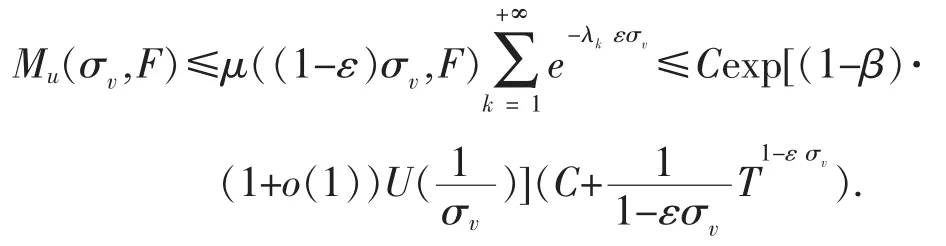
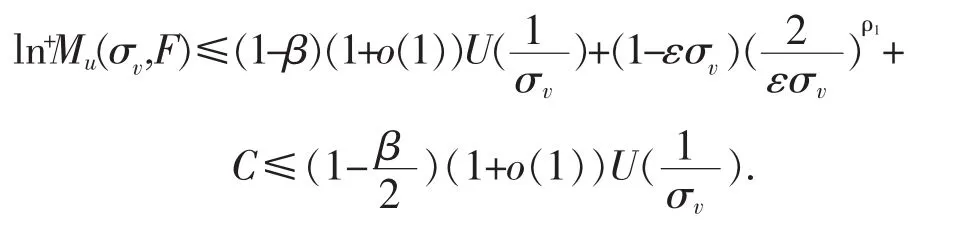
故

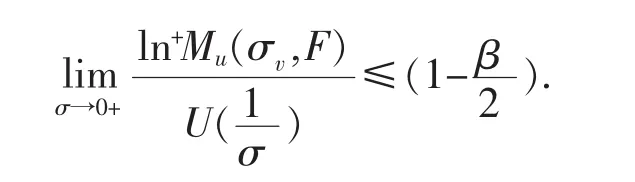
这与式（7）左边矛盾.从而定理得证.

[1]余家荣.Laplace-Stieltjes变换所定义的整函数之Borel线[J].数学学报，1963，13(3)：471-484.

[2]庄圻泰.亚纯函数的奇异方向[M].北京：科学出版社,1982.

[3]Kong Y Y，Sun D C.On type-function and the growth of Laplace-Stieltjes transformations convergent in the right half-plane[J].Adnvance Mathematics，2008，37(2)：197-205.

[4]刘名生.半平面上有限级Dirichlet级数的正规增长[J].系统科学与数学，2002，22(2)：229-238.

[5]孙道椿.半平面上的随机Dirichlet级数[J].数学物理学报，1999，19(1)：107-112.

[6]邱洋青，王建国.一类新的广义非线性集值变分包含组解的存在性问题[J].江西理工大学学报,2010，31(2)：37-40.

[7]桂贤敏，吴庆初.一类解析函数的星象性质与从属关系[J].江西理工大学学报，2008，29(2)：25-28.

[8]桂有良.半平面上有限级Laplace-Stieltjes变换的增长性[J].萍乡高等专科学校学报，2010，27(3)：6-9.

The regular growth of Laplace-Stieltjes transform of finite order in the half-plane

LAN Li-ying

（Faculty of Applied Science,Jiangxi University of Science and Technology,Ganzhou 341000,China）

In this article,the relations between the order of growth and regular growth of Laplace-Stieltjes transform of finite order in the right half-plane and the coefficients are studied under the general exponential conditions.Then the necessary and sufficient condition is obtained.

Laplace-Stieltjes transform;the type function;order;the proximate order

O174.5

A

2011-10-31

国家自然科学基金资助项目（1072607）

兰丽英（1980-），女，讲师，畲族，主要从事不确定性推理等方面的研究，E-mail：lanliying318@126.com.

2095-3046（2012）03-0094-04