含Rashba自旋轨道耦合效应的非均匀量子线的极化输运性质

徐中辉，肖贤波

（1.江西理工大学信息工程学院,江西赣州341000；2.江西中医学院计算机学院,南昌330004）

含Rashba自旋轨道耦合效应的非均匀量子线的极化输运性质

徐中辉1，肖贤波2

（1.江西理工大学信息工程学院,江西赣州341000；2.江西中医学院计算机学院,南昌330004）

采用递归格林函数法研究了含Rashba自旋轨道耦合(spin-orbit coupling,SOC)的窄-宽-窄形量子线的自旋极化输运性质.同时考虑了体系的结构和不同Rashba子带的混合对电子输运性质的影响，结果表明当电子的入射能量处在结构引起的Fano共振点时，能在出射端电极得到极化率较大的自旋极化电流，而且其大小可由自旋轨道耦合强度及系统的结构参数共同调节.这些效应说明所研究的体系也许能用来设计自旋过滤器件.

量子线；自旋极化输运；自旋轨道耦合

0 引言

量子力学告诉人们，电子除了质量和电荷以外还有另一个重要属性，就是自旋[1-3].由于现代微加工技术的需要，通过对电子电荷和电子自旋性质的研究，促进了电子学及信息技术有机结合并逐渐形成了一门新型学科即自旋电子学.近年来，随着纳米技术的不断进步大大促进了低维半导体纳米结构的研究，根据不同性能要求人们设计了很多纳米结构和半导体电子器件,比如T型电子波导[4-6]、量子线[7-8]、二维电子气[9]和量子环[10]等.这些研究很好地激发了人们对构造新型电子器件应用于量子信息存储和处理以及量子计算的兴趣，尤其是量子点系统的电子相干输运问题.另外，在周期性的电势调节下量子线或者含周期性结构的量子线中出现小的带隙和小的能带而且在磁场的调制下系统的电导重新出现量子化台阶结构[11].

自从1990年Datta和Das提出自旋场效应晶体管[12]和在实验上实现用电场来调节半导体二维电子气中Rashba自旋轨道耦合的强度[13]，各种低维纳米结构中的自旋轨道耦合效应得到了广泛的关注.最近，Xiao等人[14]研究了在含Rashba自旋轨道耦合的台阶形量子线中的自旋极化输运性质，结果发现当自旋非极化电子从窄的导线透射到宽的导线时自旋电导有很大的值,但是自旋非极化电子从宽的导线透射到窄的导线时自旋电导被很强的抑制甚至消失.其主要原因是系统在不同的偏压下有不同的电子局域态密度.此外，准一维Rashba量子线的自旋极化输运性质也得到了研究，结果表明在强Rashba自旋轨道耦合下,Rashba子带混合使得自旋电导强烈依赖电子的入射能量[15].

文中采用递归格林函数方法研究了含Rashba SOC的窄-宽-窄形量子线的自旋极化输运性质.同时考虑了系统的几何结构和不同Rashba子带的混合对电子自旋极化性质的影响，结果表明当电子的入射能量处在结构引起的Fano共振点时，能在出射端电极得到极化率较大的自旋极化电流，而且其大小可由自旋轨道耦合强度及系统的结构参数共同调节.这些效应说明所研究的体系也许能用来设计自旋过滤器件.

1 模型和计算方法

文中所研究的窄-宽-窄形量子线的结构简图如图1所示，一个横向不对称的窄-宽-窄形量子线由一个在（x，y）平面内的二维电子气在外加限制势V（x，y）的作用下形成.此二维电子气被限制在一个不对称的量子阱中，而SOC主要来自Rashba项.系统中两个窄的区域具有相同的宽度为W1，但是长度不同，分别为L1和L3，量子线中宽的部分其长度为L2，宽度为W2.利用宽度都为W1的半无限长理想导线分别连接量子线的两端.因为我们只考虑非极化注入，因此两电极是非磁性的而且无自旋轨道耦合.

图1 窄-宽-窄形量子线的结构图

利用离散化方法可以得到含有SOC的二维离散系统的紧束缚哈密顿量[15].

这里clmσ（clmσ）是（lm）格点自旋为σ的产生（湮灭）算符，εlmσ=4t是晶格的格点能量，t=h2/2m*a2为格点之间的势能，a和m*分别为电子的晶格常数和有效质量.t=α/2a表示Rashba SOC的大小.

在弹道输运中，系统的电导可以由Landauer-Buttiker[16]公式给出.根据非平衡格林函数[17]，两终端系统包含自旋的电导为

2 计算结果和讨论

利用传输矩阵法，我们计算了当Rashba自旋轨道耦合强度tso=0.189时量子线中窄区域和宽区域的电子能谱，如图2所示.

图2 自旋轨道耦合强度tso=0.189时量子线窄区域和宽区域的电子能谱

从图2（a）中可以看到能谱是线性的Rashba自旋劈裂子带.但是，在图2（b）中的能谱明显的偏离了线性的Rashba自旋劈裂.这是由于两部分的宽度不同使得该自旋轨道耦合强度在窄区域是处在弱耦合区而在宽区域是处在强耦合区[15].

为了同时考虑电子的入射能量E和Rashba自旋轨道耦合强度tso对自旋传输性质的影响，图3给出了出射端电子自旋极化率随电子入射能量和Rashba自旋轨道耦合强度的变化.从图中可以看出当电子的入射能量E＞0.4时，在右边的电极中能得到一个垂直方向的自旋极化电流.这是由Rashba自旋轨道耦合与量子线的横向传播模式之间相互耦合和横向对称性的破缺导致的[18].当电子入射到直的量子线或者空间上对称的系统中，自旋向上的电子和自旋向下的电子在纵向的透射率总是相等的，因此在出射端中Z方向的自旋极化率始终是为零的.但是，当系统在横向的对称性打破后，由于系统宽度的突变引起的量子的干涉和散射导致了自旋向上电子和自旋向下电子不对称的透射率，也就是出现自旋极化电流.这个结果可从数值计算中得到进一步的证实，我们发现G↓↑=G↑↓的关系还是成立的，但是G↑↑=G↓↓变得无效了.因此，虽然从左边电极入射的是非极化电流，但是从出射端得到的却是自旋极化电流.非常有趣的是，当电子的入射能量在0.456附近时,在右边电极可以得到一个很大的自旋极化电流.

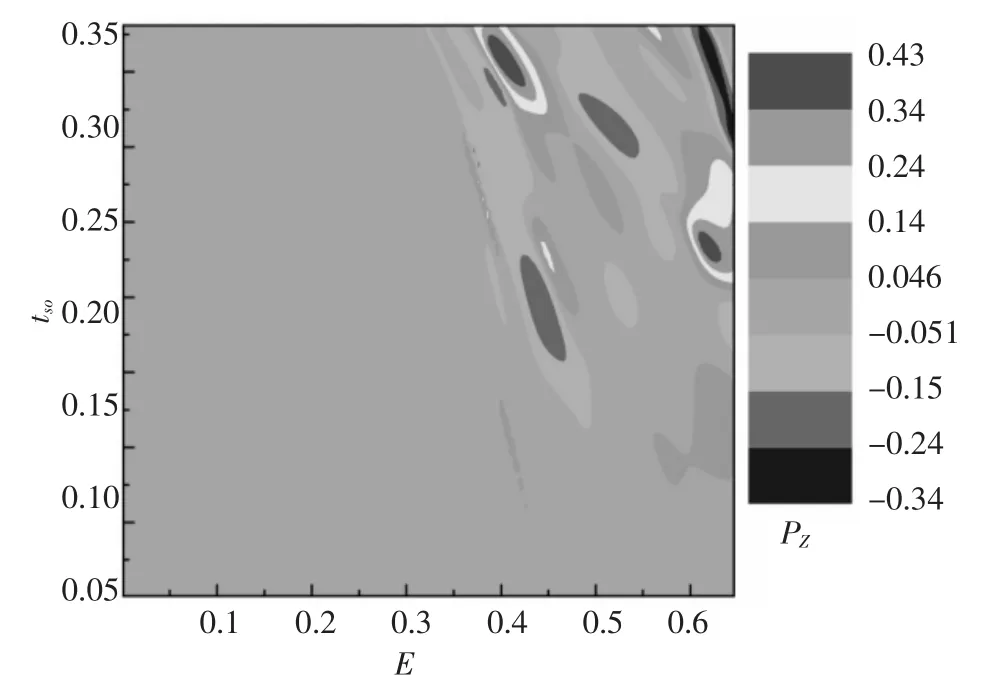
图3 出射端电子自旋极化率随电子入射能量和Rashba自旋轨道耦合强度的变化

为了进一步说明该效应,图4给出了系统总电导和相应的自旋极化率(插图)随电子入射能量的变化，其中Rashba自旋轨道耦合强度tso=0.189.可以看到系统总电导呈现台阶型结构且台阶的高度为2，在台阶的开始端都出现振荡，这是由于在量子线窄宽交界的区域形成了多次反射导致的.当入射能量E＜0.072时,由于窄区域的所有子带都是非传播模式，所以总的电导为0.当入射能量0.072＜E＜0.383时，由于在宽的区域只有最低的一对传播模式，因此在出射端不能得到自旋极化电流[19].此外，当入射能量E＞0.383时，最低的两对子带变成了传播模式，这时Rashba自旋轨道耦合与子带间的混合出现了，因此在出射端出现了自旋极化电流.值得注意的是，当入射能量处在窄区域第四对子带导通能量附近时，也就是E=0.449，总电导中出现一个“山谷”形(valley-like)的结构(见图4中的方腔内).该效应归因于量子线中的准束缚态(quasi-bound states)与连续态相互耦合.使系统的总电导出现了Fano共振结构.令人惊奇的是,在该Fano共振处自旋极化率也出现一个极大的值然，在其他一些入射能量处也出现结构引起的Fano共振（E=0.536）或者自旋轨道耦合引起的Fano共振（E=0.405），但是这些地方的自旋极化率比E=0.449处的都小.

图4 总电导随电子入射能量的变化.插图:相应的自旋极化率随电子入射能量的变化

除了系统的电导，我们根据系统的格林函数还计算了电子的局域态密度，如图5所示.其中电子的入射能量E=0.449，Rashba自旋轨道耦合强度tso=0.189.从图中可以发现在量子线左边窄的区域出现一条形状规整的带,这里一条带表示一对传播模式，在宽的区域出现了两条形状规整的带.在宽窄交界区域的右端出现了一个很明显的准束缚态(驻波).这是由于前进的波和被边界反射的波之间相互干涉形成的，而且最上面的模式更容易被占据[5].该准束缚态与Rashba自旋轨道耦合通过模式混合相互作用，这可能导致在该处出现自旋极化率很大的电流.

图5 电子局域态密度

当电子的入射能量E=0.449时，自旋极化率随Rashba自旋轨道耦合强度的变化情况如图6所示.从图中可以看出随着自旋轨道耦合强度的增大，自旋极化率也逐渐增大并在tso=0.189处达到最大值，该值和图4中插图的最大值一致.但是，随着自旋轨道耦合强度进一步增大，该Fano共振处的自旋极化率又逐渐变小.最后方向也发生了变化.这意味着可以通过自旋轨道耦合强度来调节由结构引起的Fano共振处的自旋极化率.

图6 系统的自旋极化率随Rashba SOC强度的变化；

图7 自旋极化率随右边宽区域的长度变化

系统的几何结构参数与Rashba自旋轨道耦合强度一样，也可以用来调节自旋极化率的大小.图7是自旋极化率随量子线右端窄区域长度L3的变化.其中Rashba自旋轨道耦合强度tso=0.189，其他参数与图6中相同.该图最显著的特点是在L3=10 a处出现一个“针尖”结构，自旋极化率达到最大值.此外，当L3＞13 a时,自旋极化率在0附近振荡.

3 结论

在含Rashba自旋轨道耦合的窄-宽-窄形量子线中，由于自旋轨道耦合的存在及系统在横向的对称性破缺，使得在右边的电极中产生了自旋极化的电流.特别是当电子的入射能量处在结构引起的Fano共振点时，能在出射端电极得到极化率非常大的自旋极化电流，而且其大小可由自旋轨道耦合强度及系统的结构参数共同调节.这些效应说明所研究的体系也许能用来设计自旋过滤器件.

[1]周世勋.量子力学教程[M].北京：高等教育出版社，1981.

[2]徐中辉，周详，廖昱博.量子散射的玻恩近似和程函近似[J].江西理工大学学报，2011，32(3)：37-56.

[3]李艳玲.基于腔-光纤系统制备纠缠和实现远程量子逻辑门的研究进展[J].江西理工大学学报，2011，32(3)：73-76.

[4]康裕荣，康向东.论半导体器件参数的分散性[J].江西理工大学学报，2008，29(2)：5-8.

[5]Zhai F，Xu H Q.Spin filtering and spin accumulation in an electron stub waveguide with spin-orbit interaction[J].Phys.Rev.B，2007，76(3)：35306-35310.

[6]Kiselev A A，Kim K W.T-shaped ballistic spin filter[J].Phys.Rev.B，2001，78(6)：775-777.

[7]王传奎，江兆潭.一类弯曲量子线的量子束缚态[J].物理学报，2000，49(8)：1574-1579.

[8]SunQF，XieXC.Spontaneousspin-polarizedcurrentinanonuniform Rashba interaction system[J].Phys.Rev.B，2005，71(15)：155321-155326.

[9]Pályi A，Péterfalvi C，Cserti J.Two-dimensional electron scattering in regions of nonuniform spin-orbit coupling[J].Phys.Rev.B，2006，74(7)：73305-73308.

[10]Fo¨ldi P，Kálmán O，Benedict M G，et al.Quantum rings as electron spin beam splitters[J].Phys.Rev.B，2006，73(15)：155325-155329.

[11]肖贤波，李小毛，陈宇光.含stubs量子波导系统的电子自旋极化输运性质[J].物理学报，2009，58(11)：7909-7913.

[12]Xu H Q.Electron transport through one-dimensional lateral surface superlattices in magnetic fields[J].Phys.Rev.B，1995，52(8)：5803-5812.

[13]K Nikolic，R Sordan.Electronic transport in quantum waveguide systems with attached stubs[J].Phys.Rev.B，1998，58(15)：9631-9634.

[14]Xiao X B，Chen Y G.Spin conductance control by electric means：Proposal for an all-electrical spin conductance diode[J].EPL，2010，90(4)：47004-47009.

[15]F Mireles，G Kirczenow.Ballistic spin-polarized transport and Rashbaspinprecessioninsemiconductornanowires[J].Phys.Rev.B，2001，64(2)：24426-24438.

[16]M Buttiker.Four-terminal phase-coherent conductance[J].Phys.Rev.Lett，1986，57(14)：1761-1764.

[17]T P Pareek，P Bruno.Magnetic scanning tunneling microscopy with a two-terminal nonmagnetic tip：Quantitative results[J].Phys.Rev.B，2001，63(16)：165424-165428.

[18]Zhang Z Y.Spin transmission through a mesoscopic zigzag Rashba wire[J].J.Phys：Condensed Matter，2006，19(1)：16209-16218.

[19]Zhai F，Xu H Q.Symmetry of spin transport in two-terminal waveguides with a spin-orbital interaction[J].Phys.Rev.Lett，2005，94(24)：246601-246604.

Spin-polarized transport in a nonuniform quantum wire with Rashba spin-orbit coupling

XU Zhong-hui1,XIAO Xian-bo2

(1.School of Information Engineering，Jiangxi University of Science and Technology,Ganzhou 341000,China;2.School of Computer,Jiangxi University of Traditional Chinese Medicine,Nanchang 330004,China)

The spin-polarized electron transport for a narrow-wide-narrow(NWN)quantum wire under the modulation of Rashba spin-orbit coupling(SOC)is investigated via the spin-resolved lattice Green function method.The influence of both the structure of the quantum wire and the interference between different pairs of subbands on the spin polarized electron transport is taken into account simultaneously.It is found that a very large vertical spin-polarized current can be generated by the SOC-induced effective magnetic field at the structure-induced Fano resonance.Furthermore,the magnitude of the spin polarization can be tuned by the Rashba SOC strength and structural parameters.Those results may provide an effective way to design a spin filter device without containing any magnetic materials or applying a magnetic field.

quantum wire;spin-polarized transport;spin-orbit coupling

O413.1

A

2012-03-29

国家自然科学基金资助项目(11147156)；江西省教育厅科技资助项目(GJJ12355)；江西理工大学科研基金项目计划(JXXJ11056)

徐中辉（1982-），男，在读博士，讲师，主要从事低关联系统电子输运行为等方面的研究，E-mail：longxister@163.com.

2095-3046（2012）03-0081-05