随机环境下AR型非线性时间序列的几何遍历性

王言英，苗俊红，曹秀娟

（1.山东科技大学公共课部，济南250031；2.海南师范大学数学与统计学院，海口571158）

随机环境下AR型非线性时间序列的几何遍历性

王言英1，苗俊红2，曹秀娟1

（1.山东科技大学公共课部，济南250031；2.海南师范大学数学与统计学院，海口571158）

指数自回归模型、门限自回归模型和多项式自回归模型等具有AR型非线性时间序列模型在工程中有广泛的应用.而以往研究的AR型非线性时间序列模型其干扰项为单一的白噪声序列，没有反映出动力系统受随机环境干扰的现象.文中引入随机环境的干扰，提出了随机环境下AR型非线性时间序列模型，拓宽了原模型的应用范围，增强了模型的适应性.同时利用马氏链的随机稳定性理论，研究了新模型的几何遍历性，给出了其以几何速率收敛的一个充分条件.

随机环境；几何遍历性；AR型非线性时间序列（NAR）；小集；马尔可夫链

0 引言

非线性时间序列分析可广泛地应用于经济计量、风险管理、随机服务系统、工程管理等领域，目前已成为时间序列分析理论发展的一个重要研究方向.对这类模型平稳性（遍历性）的研究一直是热门课题，例如文献[1-5].但非线性时间序列模型种类繁多,其参数辨识复杂,工程应用更为困难.相对而言,振幅依赖指数自回归模型(EXPAR模型)、门限自回归模型(TAR模型)和多项式自回归模型(PNAR模型)都是具有AR型的非线性模型,在参数辨识上比其他非线性模型更为简单,在工程中的应用较多[6].例如文献[7]研究了指数自回归模型在洪水预报中的应用；文献[8]用多项式自回归模型对非线性系统中稳定有色噪声建模；文献[9-11]把门限自回归模型应用于环境质量预报、人民币汇率波动、股票市场的研究中.

在文献[6]中研究了如下AR型非线性时间序列模型的稳定性：

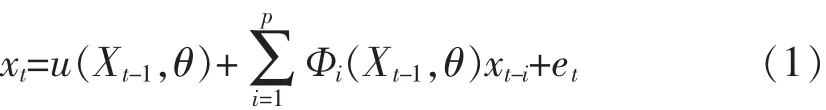
然而其干扰项为单一的白噪声序列，没有反映出动力系统受随机环境干扰的现象.文中所讨论的主要内容就是在文献[6]的基础上，引入随机环境对系统的干扰，衍生出新的模型，然后借助一般状态空间上Markov链理论，研究新模型的几何遍历性，得到了它们在某种意义下以几何速率收敛的一个充分条件，从而拓宽了原模型的应用范围，能更好的拟合实际问题.

1 模型的引入

一般地，设（Ω，H，P）是一完备的概率空间，记Rp为p维实空间，Bp为Rp上的Borel σ-代数.令E={1，2，…，r}（r∈N）为一有限集合，E的所有子集生成的σ-代数，记为F.{Zt,t≥0}为定义在（Ω，H，P）上不可约、非周期的齐次马尔可夫链，状态空间为（E，F）.{et（1）}，{et（2）}，…，{et（r）}是r个独立同分布的随机变量序列，其中每一个都定义在（Ω，H，P）上，以（Rp，Bp）为状态空间.

令Zt=Z（t）I（i）（Zt）为单点集的示性函数.

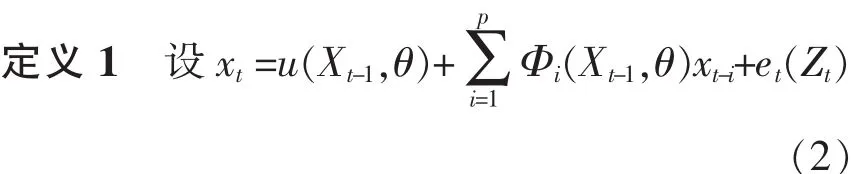
其中Xt-1=（xt-1，xt-2，…，xt-p）为系统的一个状态，u（Xt-1，θ），Φi（Xt-1，θ）为Rp→R上的光滑函数；参数θ=（θ0，θ1，…，θp）∈Θ=Θ0×Θ1×…×Θp,Θi（i=1，2，…，p）是R中的开子集，是一个参数空间.

作如下假设：A1：{zt}，{et（1）}，{et（2）}，…，{et（r）}相互独立；

则称式（2）为随机环境下的AR型非线性时间序列模型，简记为RENAR模型.

令Xt=（xt，xt-1，…，xt-p+1），Xt-1=（xt-1，xt-2，…，xt-p），F（Xt-1）=（f（Xt-1），xt-1，…，xt-p+1），α=（1，0，0，…，0）

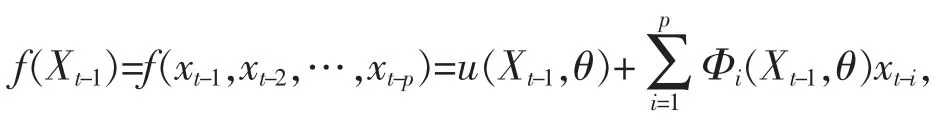
故（2）式可改写为：

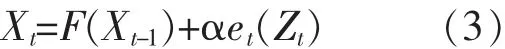
定义2[12]设模型（3）有唯一的不变概率分布π*，且对任何的初始状态X0＝，由式（3）迭代产生的概率分布记为，存在常数ρ：0＜ρ＜1，称模型（3）为伴随几何遍历的.

2 主要结论

引理1[13-14]模型（3）的导出序列{（Xt，Zt）}是定义在（Ω，H，P）上，以（RP×E，Bp×F）为状态空间的齐次马氏链.

引理2[13-14]模型（3）的导出序列{（Xt，Zt）}是μp×λ不可约和非周期的.

引理3[13-14]设{（Xt，Zt）}是模型（3）的导出A序列，A为RP中的一有界集合，且μp（A）＞0，则i∈E，A×{i}是关于{（Xt，Zt）}的小集.

注：引理2，引理3证明方法分别同文献[12]中引理1.3.2，引理1.3.3和引理1.A3.4.

证明：由引理1、引理2、引理3知，在定理给定的条件下，{（Xt，Zt）}是μ×λ不可约和A非周期的齐次马氏链，且对Rp中的一有界集合A，i∈E，A×{i}是关于{（Xt，Zt）}的小集.欲证明{（Xt，Zt）}具有几何遍历性，只需找到一个准则函数g，一个小集B和常数C1＞0，C2＞0，0＜λ＜1，使得

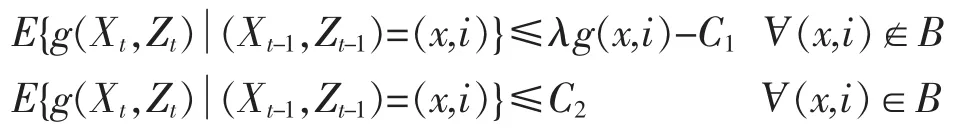
任取a1＞0，由于Φi（·，θ）≤hi（θ）＜1,

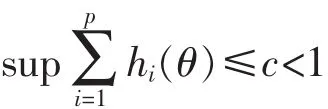
故存在a2＞0，使

从而存在a2＞0，使

存在ap-1＞0，使

存在ap＞0，使

取满足上述关系的a1，a1，…，ap，则

则0＜δ＜1,故存在λ：0＜δ＜λ＜1.

由引理3可知，K仍为{（Xt，Zt）}的小集.

故{（Xt，Zt）}是几何遍历的.

其次，将证明模型（3）本身具有伴随几何遍历性.

由前面证明知，{（Xt，Zt）}具有几何遍历性，故由定义知：存在（Rp×E，Bp×F）上的概率测度π及常数ρ：0＜ρ＜1，使

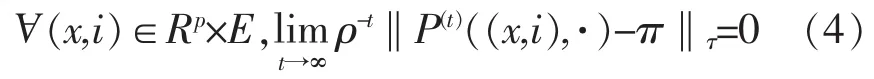
在（Rp，Bp）上，定义集合函数π*如下：AΛ∈Bp，π*（Λ）=π（Λ×E）显然，π*是（Rp，Bp）上的概率测度.

设x∈R，{Xt}是以X0=为初始值，由式（3）确定的迭代序列.于是，AΛ∈B，有

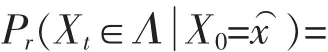
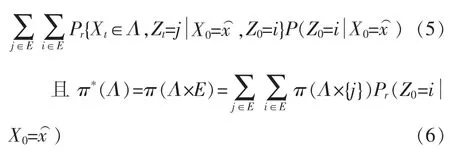
又由文献[12]中的定理1.4.1的证明过程知：π是{（Xt，Zt）}的唯一不变概率测度，从而由π*的定义易知π*是{Xt}的唯一不变概率测度.

[1]LU Zu-di，JIANG Zhen-yu.L1 geometric ergodicity of a multivariate nonlinear AR model with an ARCH term[J].Statistics&Probability Letters，2001，51(2)：121-130.

[2]Mika Meitz，Pentti Saikkonen.A note on the geometric ergodicity of a nonlinear AR-ARCH model[J].Statistics&Probability Letters，2010，80（7-8）：631-638.

[3]Zhang L X，W S Chan，S H Cheung，et al.A note on the consistency ofarobustestimatorforthresholdautoregressiveprocesses[J].Statistics&Probability Letters，2009，79(6)：807-813.

[4]王允艳，高武军，唐明田.随机环境下的幂变换门限ARMA-ARCH模型的极限行为[J].江西理工大学学报，2009，30(3)：63-65.

[5]王言英，苗俊红.随机环境下一维门限自回归TAR模型的极限行为[J].佳木斯大学学报：自然科学版，2011，29(6)：918-920.

[6]吴少敏.AR型非线性时间序列模型的稳定性分析[J].控制与决策，2000，15(3)：305-308.

[7]王文圣，丁晶，邓育仁.一类洪水预报的非线性时序模型—指数自回归模型[J].四川大学学报，1997，1(6)：1-5.

[8]林政剑，查代奉，邱天爽.非线性系统中稳定有色噪声建模及FLOC谱特性[J].计算机工程与应用，2010，46(36)：171-174.

[9]潘磊，沙斐.非线性时间序列门限自回归模型在环境空气质量预报中的应用[J].上海环境科学，2007，26(5)：213-214.

[10]靳晓婷，张晓峒，栾惠德.汇改后人民币汇率波动的非线性特征研究——基于门限自回归TAR模型[J].财经研究，2008(9)：48-56.

[11]周连强.TAR模型在沪深股票市场研究中的应用.商业时代[J].2010(21)：72-73.

[12]俞政.马氏化方法在时间序列和排队模型中的应用[D].长沙：中南大学，2003.

[13]盛昭瀚，王涛，刘德林.非线性时间序列模型的稳定性分析—遍历性理论及应用[M].北京：科学出版社，1993.

[14]安鸿志，陈敏.非线性时间序列分析[M].上海：上海科技出版社，1998.

The geometric ergodicity of AR-type nonlinear time series model under random environment

WANG Yan-ying1，MIAO Jun-hong2，CAO Xiu-juan1
(1.Department of Basic Courses，Shandong University of Science and Technology，Jinan 250031，China；2.School of Mathematics and Statistics，Hainan Normal University，Haikou 571158，China)

Exponential autoregressive models,threshold autoregressive models and polynomial autoregressive models which are AR-type nonlinear time series models are widely used in engineering.But previous studies of AR-type nonlinear time series models,the interference is a single white noise sequence,which can not reflect the factors of the interference in a system as well as the system itself influenced by sudden environment change.This article proposes a new type of AR-type nonlinear time series model under random environment,through the introduction of interference.The new model broadens the scope of application and enhances the adaptability of the model.Meanwhile,this article discussed the geometric ergodicity of the iterative sequence with the theory of stochastic stability on Markov chains and given a sufficient condition for convergence with geometric rate of the model.

random environment；geometric ergodicity；AR-type nonlinear time series；small set；Markov chain

O211.61

A

2012-03-20

海南省自然科学基金资助项目（109002）；山东科技大学“春蕾计划”资助项目（2010AZZ055）

王言英（1980-），女，讲师，主要从事非线性时间序列及统计应用等方面的研究，E-mail：feiyang5@126.com.

2095-3046（2012）03-0090-04