二维离散型随机变量独立性证明的矩阵形式

李玉梅

(怀化学院数学系, 湖南怀化 418008)

1 引言

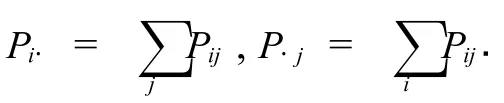
2 二维离散型随机变量独立性证明的矩阵形式

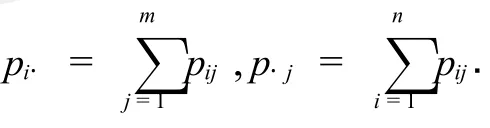
表1

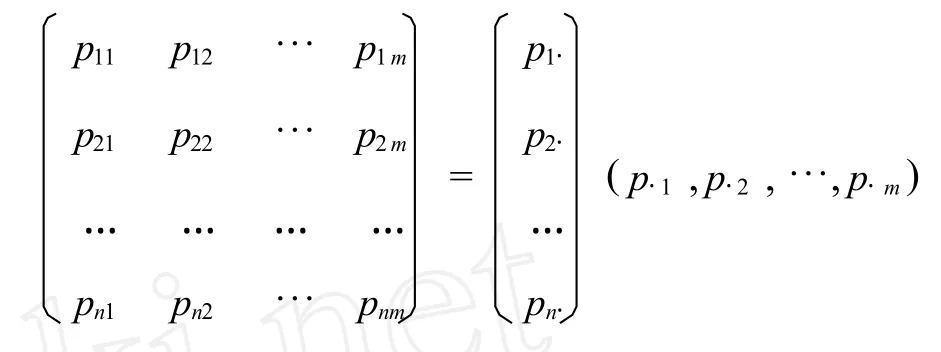
定理1[2]设二维离散型随机变量(X,Y)的联合分布列和边际分布列分别为

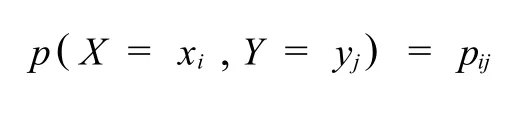
和

若 Pij= Pi·P·j对于任意的i和j(i=1,2,…,n;j=1,2,…,m)均成立,则称 X和Y相互独立.

2.1 符号标记

设二维离散型随机变量(X,Y)的联合分布列和边际分布列为表格(＊),记

显然A为二维离散型随机变量的联合分布列的矩阵形式.

令 IX=(1,1,…,1)T为n×1矩阵,IY=(1,1,…,1)为1×m矩阵.

2.2 二维离散型随机变量独立性证明的矩阵形式

定理2 设二维离散型随机变量(X,Y)的联合分布为A,则它的边际分布列分别为AIX和IYA.

证明：

随机变量 X的边际分布列.

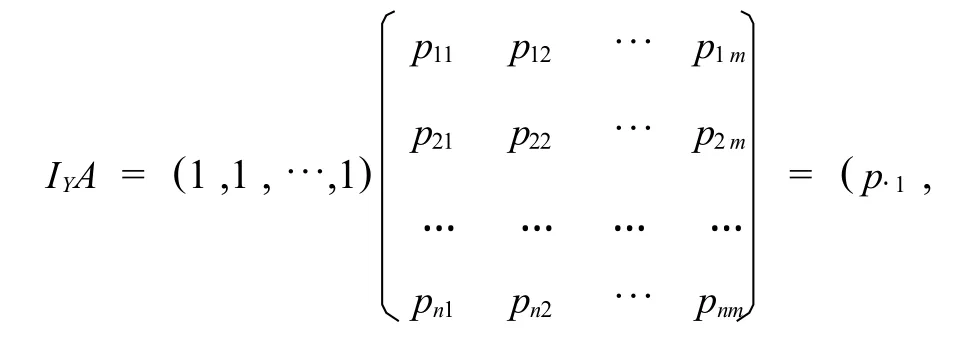
p·2,…,p·m),即为随机变量 Y的边际分布列.

定理3二维离散型随机变量 X和Y相互独立的充要条件是A=AIX·IYA

证明：“必要性” 若X,Y相互独立.则pij=pi·p·j(i=1,2,…,n;j=1,2,…,m).又(pij)=A,(pi·)=AIX,(p·j)= IYA.

故有A=AIX·IYA

“充分性” 若 A=AIX·IYA

所以有

即 pij=pi·p·j,(i=1,2,…,m),也即 X,Y相互独立.

3 利用Matlab程序判定相互独立性

%离散型随机变量独立性的Matlab验证程序

例1 已知二维离散型随机变量 (X,Y)的分布列为

images/BZ_136_1238_2511_2213_2661.png-1 3/16 3/16 3/8 1 1/32 1/32 1/16 2 1/32 1/32 1/16

问 X,Y是否相互独立?

程序运行：

ans=

随机变量 X与Y独立.

例2 设X取值0,1,Y取值0,1,2的二维离散型随机变量(X,Y)的概率分布如下表所示

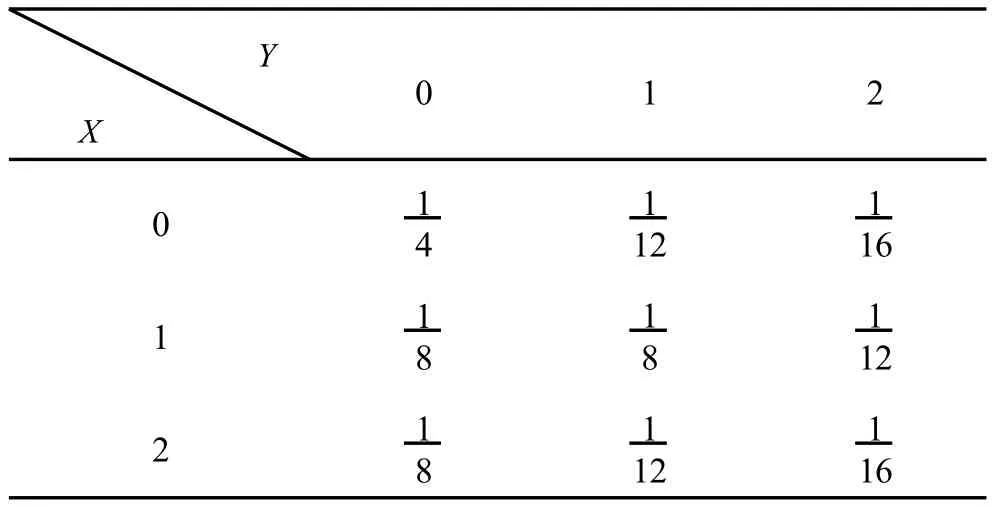
images/BZ_137_168_645_1143_854.png041216 1 1 8 1 8 1 12 2 1 8 1 1 1216

证明随机变量 X和Y不相互独立.

程序运行：

ans=

随机变量 X与Y不独立.

4 讨论

本文提出了利用二维离散型随机变量概率分布的矩阵形式来判定二维离散型随机变量的相互独立性,并利用Matlab程序快捷地做出解答.这种方法解决了一般判定二维离散型随机变量相互独立性复杂,繁琐的证明过程,并且不易出错.

[1]陈希儒.概率论与数理统计 [M].北京：科学出版社,2000：60-63.

[2]同济大学概率统计教研组.概率统计 [Z].上海：同济大学出版社,1994：85-87.