组合KdV-Burgers方程的预校算法及其数值仿真

吴红英, 燕宜佐, 王彩红

(1.怀化学院数学系,湖南怀化 418008; 2.张家界永定中学,湖南张家界 427000;3.新化县第二中学,湖南新化 417605)

1 引言

2 预测-校正算法

给出一类组合KdV-Burgers方程[6]

这里 t≥0,- ∞＜ x＜+ ∞,α,β,μ,s是常数.特别地,当β,μ=0时,上式就是标准的 KdV方程;当α,μ=0时,上式就是修正的 KdV(MKdV)方程;当β,s=0时,上式就是Burgers方程;当μ=0时,上式就是组合KdV方程,即KdV方程和MKdV方程的复合,可作为一维非线性晶格传播波的模型,也可作为流体力学中的一个模型;当β=0时,上式就是KdV-Burgers方程.

设τ为时间步长,h为空间步长,k表示空间节点,n表示时间层.记

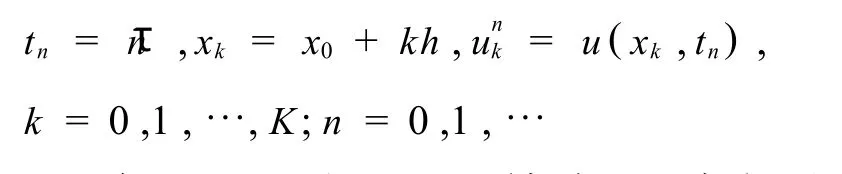
1965年Zabusky和 Kruskal针对 KdV方程 (即β,μ=0)运用向前差分技巧构造如下离散的计算格式[11,12]：

为了改善稳定性,我们运用向后差分技巧将(1)式离散为下列隐格式：

由于 (3)式是一个非线性方程组,直接求解有很大困难.运用Adams-Bashforth预测技巧和Adams-Moulton校正技巧[9],构造如下预校算法.

预测公式：

校正公式：

3 改进的预测-校正算法

为加快收敛速度、提高计算精度和保证计算稳定性,实验证明下列三种迭代策略尤其有效：多次校正的PCM算法,Gauss-Seidel迭代算法 (GS)和正反交替校正算法.

3.1 PCM算法

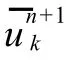
一般地,对整数 M ≥2有

3.2 Gauss-Seidel迭代算法 (GS)

校正公式：

3.3 正反交替PCM校正算法

4 仿真实例

4.1 组合 KdV-Burgers方程

给出 (1)式定义的组合KdV-Burgers方程的一个行波解[8,10]

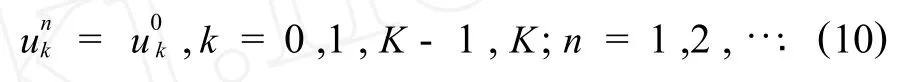
图1描绘了使用预校系统 (4)(5)、改进算法GS及正反PC2校正算法处理组合 KdV-Burgers方程的结果,它与解析解 (9)的波形完全一致.表1列出了数值解与解析解之间的误差,从计算结果可以看出误差没有扩大,算法具有很好的稳定性.

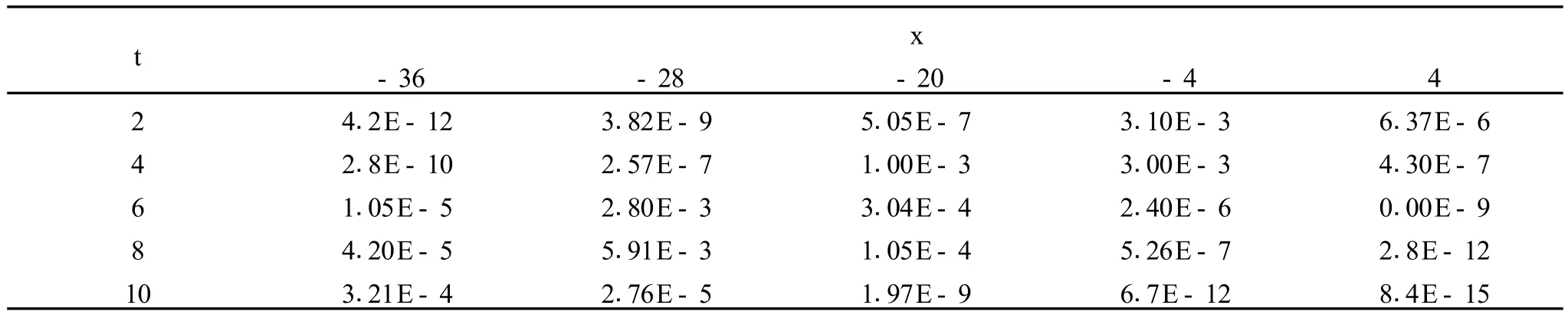
表1 组合KdV-Burgers方程数值解与精确解之间的误差

如果采用预校系统 (4)(5)及PC1校正算法处理,波形与解析解基本一致,但数值解与解析解之间出现较大的相位差.

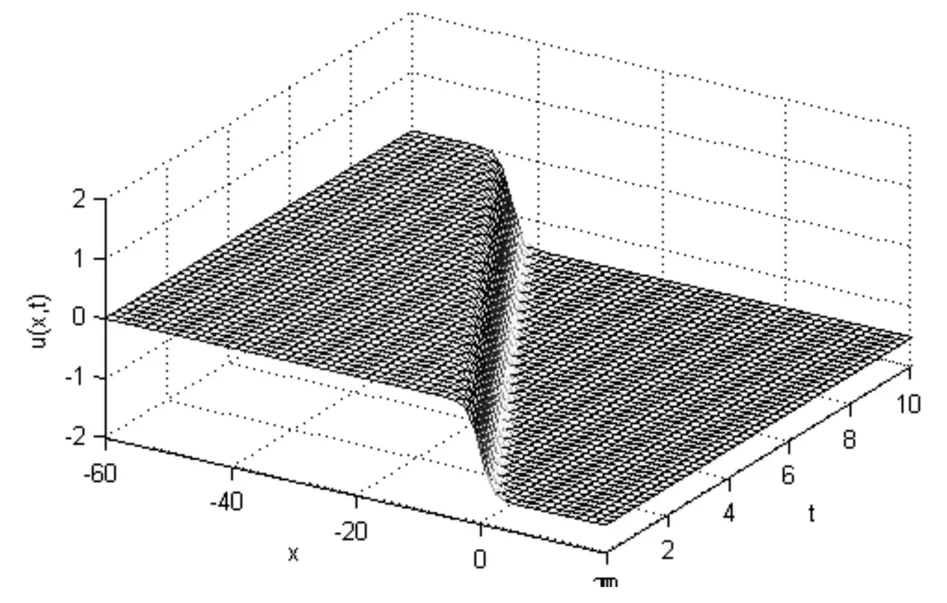
图1 组合KdV-Burgers方程中一个行波运动的情形

4.2 KdV-Burgers方程

给出 (1)式定义的 KdV-Burgers一个行波解[10,13]

取参数

α =1,β =0,μ =2,s=-1,C=24/25,l=0,h=0.1,τ=0.0001,-20 ≤ x≤40.

图2描绘了使用预校系统 (4) (5)、改进算法GS及正反PC2校正算法处理KdV-Burgers方程的结果,它与解析解 (11)的波形十分吻合,误差小于0.0053.

图3描绘了使用预校系统 (4) (5)、改进算法GS及正反PC2校正算法处理KdV-Burgers方程中两个行波交互的结果,它与解析解

的波形十分吻合,误差小于0.0046.这里参数为

α=1,μ=2,s=-1,C1=24/25,l1=-20,C2=-24/25,l2=20,h=0.1,τ=0.0001,-30 ≤ x ≤40,0≤t≤30.

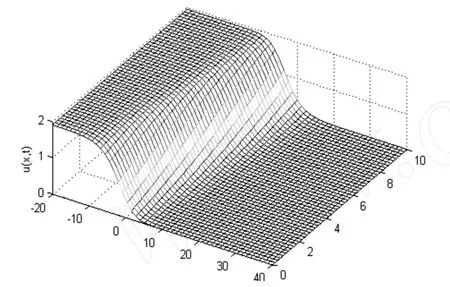
图2 KdV-Burgers方程中一个行波运动的情形

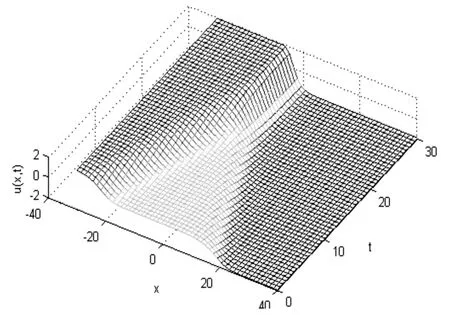
图3 KdV-Burgers方程中两个行波交互的情形

4.3 KdV方程

当α=6,s=-1,β=0,μ=0时 ,方程 (1) 是标准的KdV方程,在初值 u(x,0)=6sech2(x)和周期边界 u(-20,t)= t(20,t)条件下,有双孤立波解[12].选取时间步长τ=0.0001,空间步长 h=0.2.

(ⅰ)用Zabusky和Kruskal提出的计算格式 (2)进行数值模拟,当t=1.8时波形开始不稳定,见图4,无法观察孤立波的第2次碰撞过程.(ⅱ)改用预测-校正公式 (4)- (5),t=4秒时模拟结果仍保持稳定的波形.如图5,在t=3.3时两个孤立波开始碰撞;t=3.6时,大孤子完全“吞噬”了小孤子;t=3.7时,两孤子相互分离,并保持原来的形状;整个碰撞过程中,与线性叠加不同,振幅没有增加,反而有所减小,较好地模拟了非线性孤立波的传播与碰撞过程,改进了(2)式不能长时间模拟的缺陷.(ⅲ)实验表明,综合运用改进的预测 -校正公式(6)-(8)在较大步长τ=0.0003和更长时间t=10内模拟均不出现数值振荡,且精度较高.

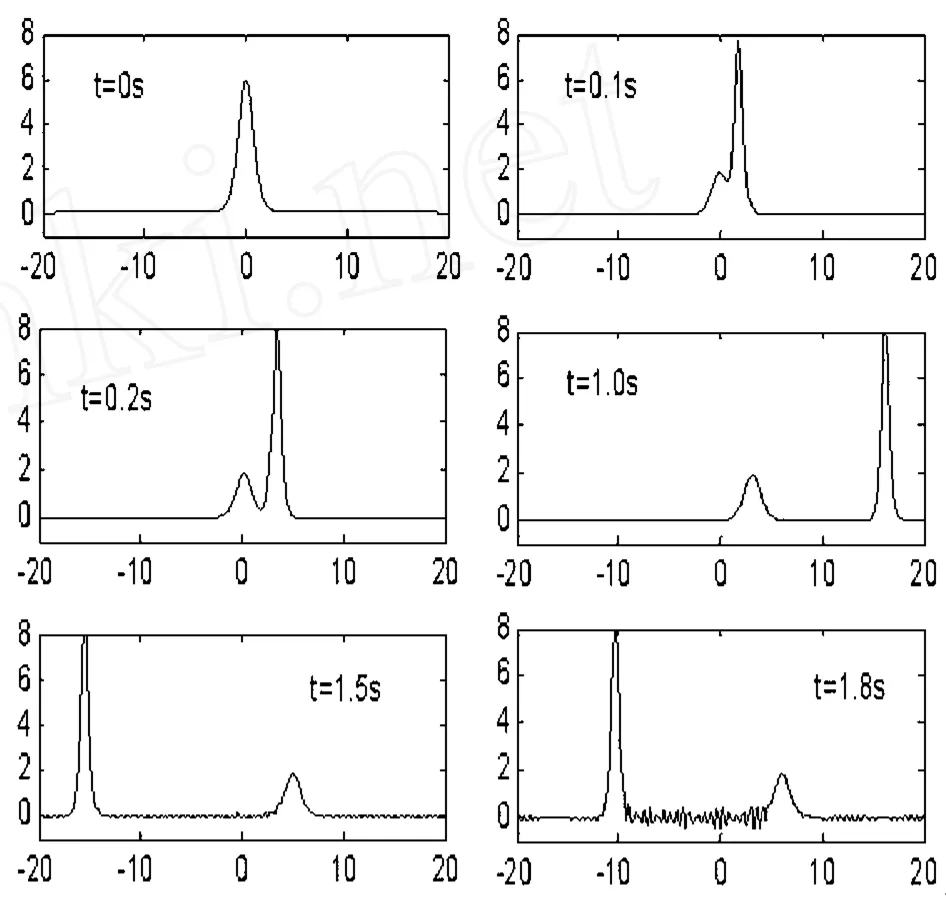
图4 用Zabusky和Kruskal提出的计算格式模拟 KdV方程双孤立波解的数值结果,短时间出现振荡

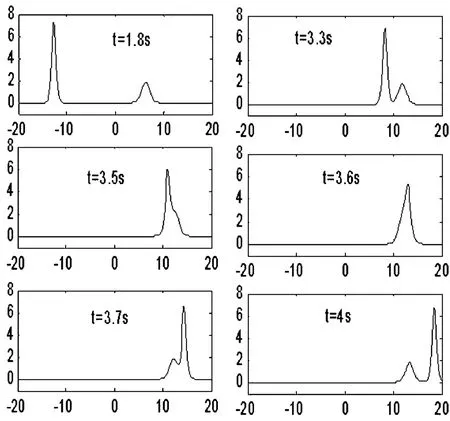
图5 用预测-校正算法模拟KdV方程双孤立波解的数值结果,长时间稳定

[1]Scott-Russell J.Report on waves[R].In：rep.14th Meet.Br.Ass.Advmt.Sci.,1845：311-390.

[2]K orteweg D J and ViresG.De.On the change of form of long waves advancing in a rectangular channel,and a new type of long stationary wave[J].Phil.Mag.,1895,539：422-443.

[3]Drazin P G and Johnson R.S.Solitons：An Introduction[M].Cambridge：University Press,1989.

[4]Dodd R K,Eilbeck J E,G ibbons J D and Morris H C.Solitons and non-linear wave equations[M].London：Academic Press,1982.

[5]FornbergB and Whitham G B.A numerical and theoretical study of certain non-linear wave phenomena[J].Phil.Trans.R.Soc.London,1978,289(A)：373-404.

[6]Taha T R and Ablowitz M J.Analytical and numerical aspects ofcertain nonlinearevolution equations.II.Numerical,korteweg-de Vries equation[J].J.Comp.Phy.,1984,55：231-253.

[7]Shokin Y I.The method of differential approximation.[M]Springer,Berlin,Heidelberg,New York,1983.

[8]Wang Mingliang,Exact solutions of a compound KdV-Burgers equation[J],Physics Letters,1996,213(A)：279-287.

[9]Stoer J and Bulirsch R.Introduction to numerical analysis[M].Springer,Berlin,Heidelberg,New York,1976.

[10]左进明,周运明,等.一类组合 KdV-Burgers方程的数值解法 [J].山东大学学报,2006,41(4)：49-52.

[11]王雨顺,王 斌,季仲贞.孤立波方程的保结构算法[J].计算物理,2004,21(5)：386-400.

[12]赵平福.KdV方程保结构算法 [D].北京：中国科学院数学与系统科学院,2000：59-64.

[13]徐昌智,郑春龙.KdV-Burgers方程和Schrding KdV耦合方程的显示行波解 [J].贵州师范大学学报,2003,21(3)：43-47.