基于密度泛函理论计算的丙烷脱氢动力学

李 庆，杨明磊，隋志军，朱贻安，周兴贵

（华东理工大学 化学工程联合国家重点实验室，上海 200237）

基于密度泛函理论计算的丙烷脱氢动力学

李 庆，杨明磊，隋志军，朱贻安，周兴贵

（华东理工大学 化学工程联合国家重点实验室，上海 200237）

采用乙二醇还原法制备了Pt颗粒粒径为6 nm的Pt/Al2O3催化剂，借助密度泛函理论（DFT）计算的动力学参数，建立了 Pt(111)面上的微观反应动力学模型，并在此基础上建立了 Pt(111)面上的 Langmuir-Hinshelwood Hougen-Watson(LHHW)模型。结果表明：丙烷脱氢对丙烷的反应级数是1.00级，对氢气的反应级数是-0.51级；反应的表观活化能约为80 kJ/mol；在Pt(111)面上，氢原子是最丰富的表面吸附物种，丙烷脱氢速率受第二步脱氢控制。

丙烷脱氢 密度泛函理论 动力学

工业上丙烷脱氢生产丙烯常用催化剂有Pt-Sn/Al2O3和Cr2O3/Al2O3。在Pt催化剂上，丙烷脱氢生成丙烯一般包括丙烷的吸附，丙烷一步脱氢和二步脱氢，丙烯的脱附以及氢气的脱附。一般认为丙烷在Pt催化剂表面的脱氢是速率控制步骤，由于脱氢分两步进行，哪一步脱氢是速率控制步骤尚存争议[1-4]，因而有必要对Pt催化剂上丙烷脱氢机理进行研究，从而建立可靠的动力学模型，为反应器的设计和过程优化提供基础。获得动力学模型参数的传统方法是对实验数据进行回归，为确保模型参数的可靠性，需要大量的实验数据。本工作尝试采用一种新的动力学研究方法：即利用密度泛函理论（Density Functional Theory，简称 DFT）计算确定各基元反应的动力学参数，进行微观反应动力学分析，在此基础上推导出Langmuir-Hinshelwood Hougen-Watson（LHHW）型动力学模型。与传统的动力学研究方法相比，该方法可减少实验量，得到的动力学参数也具有明确的物理意义。

1 实验部分

1.1 催化剂制备

Pt/Al2O3催化剂制备方法如下：首先将一定比例的乙二醇和去离子水的混合溶液倒入三口烧瓶，再加入氧化铝（γ-Al2O3, Pural 200）的乙二醇悬浊液，最后加入一定量氯铂酸（H2PtCl6·6H2O）的乙二醇溶液。将以上混合物搅拌过夜后用浓度为2 mol/L的氢氧化钠乙二醇溶液将混合物的pH值调至13，然后在氩气保护下继续搅拌并升温至130 ℃进行还原。还原4 h后，冷却至室温，用盐酸（浓度2 mol/L）调节pH值至3，继续搅拌2 h。离心分离得到催化剂固体后，用大量去离子水洗涤除去Na+和乙二醇，直至洗涤液为中性。离心得到的固体在103 ℃下干燥4 h，制得催化剂。

1.2 催化剂表征

采用原子吸收光谱（ICP-AES）法分析Pt的负载量；采用N2吸附（ASAP 2010，Micrometrics）测催化剂的BET比表面积；采用氢气化学吸附（H2-Chemisorption, AutoChem 2920，Micrometrics）分析催化剂Pt分散度；采用日本JEOL JEM 2010型透射电镜（TEM）确定Pt粒子的大小。

1.3 催化剂评价

采用固定床管式反应器对催化剂进行评价。催化剂装填量为0.1 g，反应前，催化剂在500 ℃，流量为10 mL/min的纯氢气中还原100 min，然后切换至反应气体。反应气体总流量为90～170 mL/min，丙烷、丙烯和氢气在进料中的物质的量的浓度均控制在10%以内（氩气作为惰性气体），反应温度为450～490 ℃。在该反应条件下，内外扩散的影响已经排除[3]。本研究所选的动力学实验温度较工业应用低，且氢气分压相对较高，以在保持催化剂具有一定活性的同时又可避免催化剂快速失活。

1.4 DFT计算

使用DFT计算相关动力学参数。Pt(111)面是基于p(3 × 3)超胞建立。该表面模型包含四层Pt金属原子。当一个基团置于Pt(111)表面上时，其在表面上的覆盖率为1/9单层（monolayer）。具体的模型建立和计算细节参考文献[5,6]。

2 动力学模型

微观动力学模型包含了丙烷脱氢生成丙烯的五个基元步骤，分别为丙烷的物理吸附、第一步脱氢、第二步脱氢、丙烯的脱附和氢气的脱附，具体反应式见（1）～（5）：

各基元步骤的速率常数均由DFT计算而得的熵变和活化能计算得到，计算公式见式（6）和（7）：

其中，kB和h分别为波尔兹曼常数和普朗克常数。对吸附过程，活化能为0；对脱附过程，活化能为吸附热。

分别假设第一、第二步脱氢为速率控制步骤，其他基元步骤均处于平衡态，得到两个LHHW模型，分别为式（8）和（9）[3]。在计算反应结果时，反应器模型为拟均相一维平推流模型。

式中，Keq为丙烷脱氢反应平衡常数，其计算公式为：

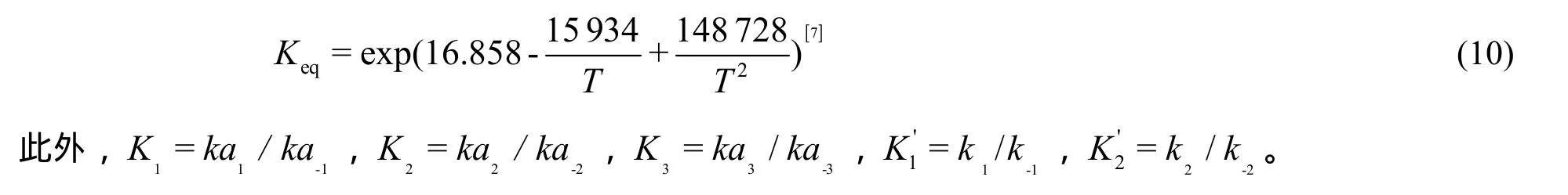
3 结果与讨论

3.1 实验结果

催化剂表征结果表明Pt的负载量为1.2%，BET比表面积69.6 m2/g，Pt分散度18.8%。采用氢气化学吸附和透射电镜测得催化剂的粒径分别为5.9和6.0 nm，两种粒径表征结果基本一致。

丙烷脱氢反应速率表达的幂形式如式（11）所示。

结婚前，周有光有些忧虑地给张允和写信说：“我很穷，怕不能给你幸福。”张允和回了一封很长的信，表明了一个意思：幸福是要自己去创造的！

式中：A为速率常数指前因子；R为理想气体常数；T为反应温度，K；Ea为表观反应活化能，kJ/mol；m和n分别为丙烷和氢气的表观反应级数。

在一定温度和氢气分压下，对式（11）两边取自然对数可得：

在一定温度和丙烷分压下，对式（11）两边同时取自然对数可得，

而在一定的丙烷、氢气分压下，对式（11）两边同时取自然对数可得，

其中，C1，C2和C3均为常数项。

本研究中，丙烷脱氢反应速率通过转化频率（TOF）来计算。由于每次实验丙烷转化率均小于5%，因此，丙烯生成反应的TOF可以通过式（15）进行计算。

图 1 表观反应级数和活化能的实验结果与模拟结果比较Fig.1 Comparison of experimental results and simulation results of apparent reaction orders and activation energies

3.2 微观动力学结果

一般情况下，可以认为催化剂中Pt粒子的形状接近切角八面体[8-10]，图2给出了切角八面体形状的Pt粒子上各晶面比例随着Pt粒径的变化。由图2可见，当Pt粒子大于6.0 nm时，Pt(111)面占绝大多数。

根据丙烷脱氢过程中 DFT的相关研究[5,6]，Pt(211)与 Pt(100)面上第一步和第二步脱氢活化能均在25～40 kJ/mol，而Pt(111)面上对应的脱氢活化能则为68 kJ/mol左右，且丙烯进一步脱氢生成深度脱氢产物的活化能在Pt(211)与Pt(100)面上分别约为41和52 kJ/mol，而在Pt(111)面上则约为73 kJ/mol。由此可见，丙烷更容易在Pt(211)与Pt(100)面上发生深度脱氢，深度脱氢产物易发生C-C键断裂，从而导致晶面被积炭覆盖。DFT计算的Pt(111)面以及积炭覆盖的Pt(211)，Pt(100)面上的丙烷的第一步脱氢的反应活化能分别为66.6，81.0和61.8 kJ/mol，第二步脱氢的反应活化能分别为67.5，70.4和60.8 kJ/mol。又考虑到Pt(111)面的百分比远比其他两个面高，所以本研究把 Pt(111)面作为催化面进行计算，建立了 Pt(111)面上的丙烷脱氢微观反应动力学模型，以该模型模拟本研究所使用的催化剂上的丙烷脱氢反应。Pt(111)面上的各动力学参数采用DFT计算的方法[5,6]得到，具体列于表 1（表中各数值除氢气吸附热之外均在氢原子覆盖度为零的情况下计算得到）。与文献报道的丙烷[11]和氢气[12-15]在 Pt(111)面上的吸附热相比，本研究得到的丙烷和氢气的吸附热与文献中报道的数值基本吻合，而文献报道的丙烯吸附热[11,16,17]为30～80 kJ/mol，与本研究所得的93.6 kJ有一定差异，这可能是DFT计算模型以及函数对本体系准确度的原因。

图 2 Pt颗粒粒径与表面晶面组成的关系（Pt(211)代表位于边和顶点处的原子）Fig.2 The relationship between surface facet composition and Pt particle size(Pt(211) represents Pt atoms located at the edge or the corner)

表1 DFT计算的各基元步骤熵变和活化能Table 1 DFT calculated entropy changes and activation energies of each elementary reaction

为确保动力学模拟的准确性，在进行模拟时对所有基元步骤的动力学数据进行了强制热力学一致性处理。即首先通过查表获得丙烷、丙烯和氢气的热容数据[18]，由此可计算任意反应温度下总反应的熵变和焓变。将由DFT计算的总反应熵变和焓变与通过查表计算的总熵变和焓变进行比较并作差。结果显示，DFT计算的总反应的熵变与实际数据很接近，仅高出2.3～2.6 J/(mol·K)；而DFT计算的总焓变则比实际值高出25～26 kJ/mol。为了达到热力学一致性，本研究将DFT计算的总反应熵变与实际总反应熵变的差值通过拉格朗日乘子法平均分配到每个基元反应的正反应熵变中。对于反应焓变的调节，根据以上讨论，计算的总反应的反应热比实际反应热高出25～26 kJ/mol，本研究计算的丙烯的吸附热高于文献平均值37.8 kJ/mol，而丙烯吸附热的计算偏差是导致反应焓变发生偏差的主要原因，因此，可通过调节丙烯吸附热的方式使反应焓变达到热力学一致。

微观反应动力学模拟结果显示，在Pt(111)面上，第二步脱氢是速率控制步骤，吸附的氢原子是表面最丰富物种（表2）。微观反应动力学模拟预测的反应级数和活化能与实验值的比较如图1所示。模型预测的丙烷、氢气表观反应级数分别为1.00和-0.53级，与实验值十分接近；表观活化能的模型预测值为109.3 kJ/mol，略高于实验值。

表2 Pt(111)面上不同物种的表面覆盖Table 2 Surface coverage of different species on Pt(111)

3.3 LHHW模型结果

两个LHHW动力学模型在忽略逆反应和各气体吸附对净反应速率影响的情况下，可以得到简化的模型见式（17）和（18），并可知当第一步脱氢为速率控制步骤时，丙烷脱氢反应对丙烷的反应级数是一级，对氢气的反应级数是零级；当第二步脱氢为速率控制步骤时，丙烷脱氢反应对丙烷的反应级数是一级，对氢气的反应级数则是-0.5级。结合本实验结果可推测，在Pt粒径为6.0 nm的Pt/Al2O3催化剂上的丙烷脱氢反应速率很可能是由第二步脱氢控制的，因为氢气的反应级数是-0.51。同时，Pt(111)面上的微观反应动力学模拟结果也显示第二步脱氢是速率控制步骤。因此，本工作采用模型M-II来模拟丙烷脱氢在Pt/Al2O3催化剂上的动力学。模型参数来自于DFT计算，模型预测的反应级数和活化能如图1所示。由图1可知，模型预测的丙烷、氢气表观反应级数分别为1.00和-0.73级，丙烷反应级数的预测值与实验值一致，而对于氢气反应级数的绝对值而言，预测值明显高于实验值；表观活化能的模型预测值为131.5 kJ/mol，高于实验值50.8 kJ/mol。

综上所述，无论是微观反应动力学模型还是LHHW模型，都能较好地预测丙烷的表观反应级数；两模型预测的氢气表观反应级数的绝对值和表观活化能普遍高于实验值。其中，微观动力学模型的预测结果与实验值较为接近。而模拟值与实验值之间的差异主要来源于模型催化剂与实际催化剂间的差异，模型模拟的是Pt(111)面上的丙烷脱氢过程，但实际的催化剂并非理想的只含Pt(111)面的单晶催化剂，它还包含Pt(100)和Pt(211)等晶面，从而导致两个模型模拟的结果与实验值有所不同。此外，微观反应动力学模型反映了Pt(111)面上所有基元反应的反应速率，而LHHW模型则假设了第二步脱氢为速率控制步骤，其他基元反应都达到平衡状态。

根据LHHW模型并结合表观反应级数和活化能的定义式（19）和（20），可以理论推导出丙烷、氢气反应级数以及表观反应活化能的数学表达式（式（21），（22）和（23））。需要注意的是，由于丙烷、丙基以及丙烯的表面覆盖度很小，所以在推导过程中将以上三者的表面覆盖度视为零。

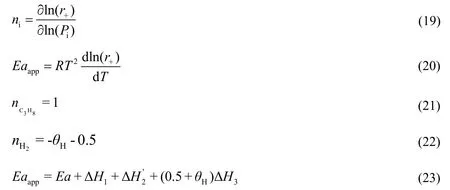
式中：Ea为正反应活化能，kJ/mol；ΔH1为丙烷吸附热，kJ/mol；为第一步脱氢反应的反应热，kJ/mol；ΔH3为氢气吸附热，kJ/mol；Hθ为氢原子的表面覆盖度。

由式（21）～（23）可知，丙烷的反应级数始终是1.00级；氢气的反应级数决定于氢原子表面覆盖度；反应的表观活化能则与Ea，，ΔH3和Hθ有关。将经过热力学一致性检验后的DFT计算的各气体吸附热以及微观反应动力学模拟得出的氢原子表面覆盖度代入上式（18）和（19），可得氢气的反应级数和表观活化能分别为-0.74和126.1 kJ/mol，与LHHW模型模拟结果（反应级数为-0.73，表观活化能为131.5 kJ/mol）基本一致。

4 结 论

本工作利用DFT计算结果建立了Pt催化丙烷脱氢反应的微观反应动力学模型，该模型可以较好地预测实验结果，可获得催化剂表面物种覆盖度，速率控制步骤等信息，而基于微观反应动力学建立的LHHW模型在预测实验数据时具有一定的精度，不失为一个实用的动力学模型。联系微观反应动力学和LHHW动力学，发现丙烷表观反应级数总是1.00级，氢气的表观反应级数则与氢原子表面覆盖度有关，反应的表观活化能与第二步脱氢反应的正反应活化能、丙烷吸附热、第一步脱氢反应的反应热、氢气吸附热以及氢原子的表面覆盖度有关。DFT计算可以作为动力学参数的来源，但在使用时一方面需要注意实际催化剂的非理想性，另一方面还需注意DFT计算本身所具有的局限性。

[1]Biloen P, Dautzenberg F M, Sachtler W M H. Catalytic dehydrogenation of propane to propene over platinum and platinum-gold alloys[J].Journal of Catalysis, 1977, 50(1): 77-86.

[2]Jackson D, Grenfell S J, Matheson I M, et al. Modelling of alkane dehydrogenation under transient and steady state conditions over a chromia catalyst using isotopic labeling[J]. Studies in Surface Science and Catalysis, 1999, 122: 149-155.

[3]Li Q, Sui Z J, Zhou X G, et al. Kinetics of propane dehydrogenation over PtSn/Al2O3catalyst[J]. Applied Catalysis A: General, 2011, 398(1-2):18-26.

[4]Suzuki I, Kaneko Y. Dehydrogenation of propane over chromia-alumina-potassium oxide catalyst[J]. Journal of Catalysis, 1977, 47(2):239-248.

[5]Yang M L, Zhu Y A, Fan C, et al. DFT study of propane dehydrogenation on Pt catalyst: effects of step sites[J]. Physical Chemistry Chemical Physics, 2011, 13: 3257-3267.

[6]Yang M L, Zhu Y A, Fan C, et al. Density functional study of the chemisorption of C1, C2 and C3 intermediates in propane dissociation on Pt(111)[J]. Journal of Molecular Catalysis A: Chemical, 2010, 321(1-2): 42-49.

[7]Sint Annaland van M, Scholts H A R, Kuipers J A M, et al. A novel reverse flow reactor coupling endothermic and exothermic reactions. Part II: sequential reactor configuration for reversible endothermic reactions [J]. Chemical Engineering Science, 2002, 57(5): 855-872.

[8]Barnard A S, Lin X M, Curtiss L A. Equilibrium morphology of face-centered cubic gold nanoparticles ＞3 nm and the shape changes induced by temperature[J]. The Journal of Physical Chemistry B, 2005, 109(51): 24465-24472.

[9]Van Hardeveld R, Hartog F. The statistics of surface atoms and surface sites on metal crystals[J]. Surface Science, 1969, 15(2): 189-230.

[10]Patil A N, Paithankar D Y, Otsuka N, et al. The minimum-energy structure of nanometer-scale gold clusters. zeitschrift für physik d atoms[J].Molecules and Clusters, 1993, 26(1): 135-137.

[11]Nykänen L, Honkala K. Density functional theory study on propane and propene adsorption on Pt(111) and PtSn alloy surfaces [J]. The Journal of Physical Chemistry C, 2011, 115(19): 9578-9586.

[12]Watwe R M, Cortright R D, Nørskov J K, et al. Theoretical studies of stability and reactivity of C2 hydrocarbon species on Pt clusters, Pt(111),and Pt(211)[J]. The Journal of Physical Chemistry B, 2000, 104(10): 2299-2310.

[13]Spiewak B E, Cortright R D, Dumesic J A. Microcalorimetric studies of H2, C2H4, and C2H2adsorption on Pt powder[J]. Journal of Catalysis,1998, 176(2): 405-414.

[14]Sharma S B, Miller M T, Dumesic J A. Microcalorimetric study of silica-and zeolite-supported platinum catalysts[J]. Journal of Catalysis,1994, 148(1): 198-204.

[15]Podkolzin S G, Watwe R M, Yan Q, et al. DFT calculations and monte carlo simulations of the Co-adsorption of hydrogen atoms and ethylidyne species on Pt(111)[J]. The Journal of Physical Chemistry B, 2001, 105(36): 8550-8562.

[16]Valcárcel A, Ricart Josep M, Clotet A, et al. Theoretical study of the structure of propene adsorbed on Pt(111)[J]. Surface Science, 2002,519(3): 250-258.

[17]Valcárcel A, Ricart Josep M, Clotet A, et al. Theoretical study of dehydrogenation and isomerisation reactions of propylene on Pt(111)[J].Journal of Catalysis, 2006, 241(1): 115-122.

[18]Smith J M, Ness H C, Abbott M M. 化工热力学导论[M]. 刘洪来, 陆小华, 陈新志. 北京: 化学工业出版社, 2008: 423-424.

Kinetics of Propane Dehydrogenation Based on Density Functional Theory

Li Qing, Yang Minglei, Sui Zhijun, Zhu Yi’an, Zhou Xinggui
(State Key Laboratory of Chemical Engineering, East China University of Science and Technology, Shanghai 200237)

Pt/Al2O3catalyst with Pt particle size of 6 nm was prepared by ethylene glycol reduction method and the kinetics of propane dehydrogenation was then studied under atmospheric pressure and at 450-490 ℃. The apparent reaction orders for propane and hydrogen were the first and minus half, respectively, and the apparent reaction activation energy was about 80 kJ/mol. Based on Density Functional Theory(DFT) calculation, a microkinetic model was established on Pt(111) facet, where the kinetic simulation was carried out. The simulation indicated that the adsorbed hydrogen atom was the most abundant surface intermediate and that the reaction rate was limited by the second hydrogen elimination. A Langmuir-Hinshelwood Hougen-Watson(LHHW) model was subsequently obtained based on the information provided by microkinetics. Compared with conventional kinetic model, the models established in this study were superior in the reliability of the mechanism indicated by DFT calculation and the convenience of the acquisition of the kinetic parameters. The simulation also indicated that the models could well predict the experiments.

propane dehydrogenation; Density Functional Theory; kinetics

TQ323.8 文献标识码：A

1001—7631 ( 2012 ) 02—0097—07

2012-01-05；

2012-04-20

李 庆（1984-），男，博士研究生；隋志军（1974-），男，副教授，通讯联系人。E-mail: zhjsui@ecust.edu.cn

国家973计划（2012CB720500）