一类分数阶耦合系统多点边值共振问题解的存在性

张 宁，张 娣，史小艺

(1.中国矿业大学理学院，江苏徐州 221116;2.中国矿业大学管理学院，江苏徐州 221116)

0 引言

近些年来，分数阶导数及分数阶微分方程在科学、工程和数学等领域得到了重要应用.在分数阶微分方程边值问题研究上，科研人员获得了不少研究成果［1-9］.值得注意的是，分数阶耦合系统多点边值共振问题作为分数阶非局部边值问题的一种特殊情况，近年来得到许多研究人员的重视，一些学者运用Mawhin的连续性定理来研究多点边值问题，如文献［4］就研究了耦合系统的3点边值共振问题，

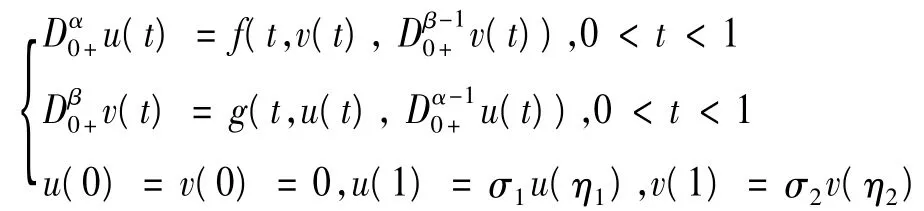
其中，1＜α，β≤2，0＜η1，η2＜1，σ1，σ2＞0，σ1ηα-11=σ2ηβ-12=1，f，g:［0，1］×R2→R连续，Dα0+是标准Riemann-Liouville分数阶导数.

受其启发，本文研究分数阶非线性微分方程耦合系统多点边值共振问题，

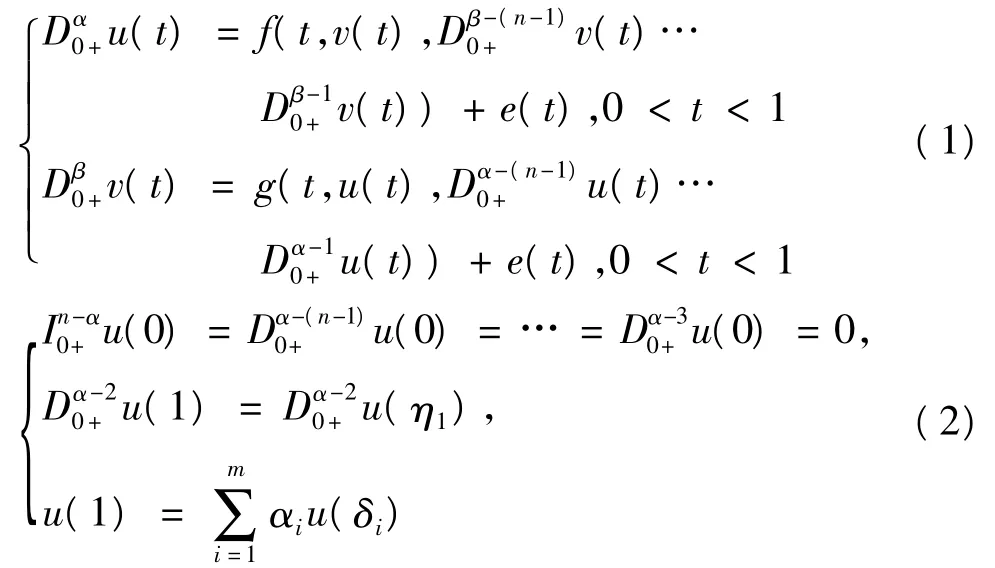
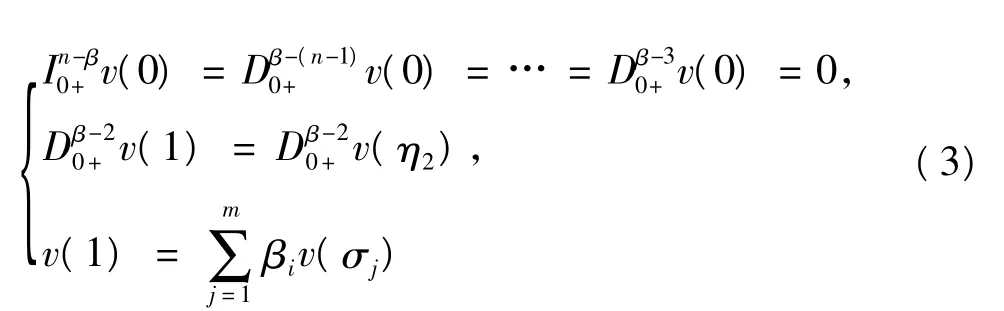
其中，n＞2是自然数，n-1＜α，β≤n，0＜η1，η2＜1，0＜δ1＜…＜δm＜1，0＜σ1＜…＜σm＜1，αi，βi∈R，Dα0+和Iα0+分别是标准Riemann-Liouville分数阶导数和积分，f，g:［0，1］×Rn→R满足Caratheodory条件，e(t)∈L1［0，1］.令，

1 预备知识

设Y，Z是实Banach空间，L:domL⊂Y→Z是一个指标为零的Fredholm算子，P:Y→Y，Q:Z→Z，是连续投影算子且满足ImP=Kerl，KerQ=ImL，Y= KerL⊕KerP，Z=ImL⊕ImQ.则映射，L|domL∩KerP: domL∩KerP→ImL，是可逆的，记这个映射的逆映射为KP，令N:Y→Z是一个映射，Ω是Y的一个有界开集且满足，domL∩Ω=＞，如果QN(Ω—)有界，KP(I-Q)N:Ω—→Y是紧的，则称N是L-紧的，设J: ImQ→KerL是一个线性同构.

定义1［1］函数y:(0，+∞)→R的α阶Riemann-Liouville分数阶积分为，

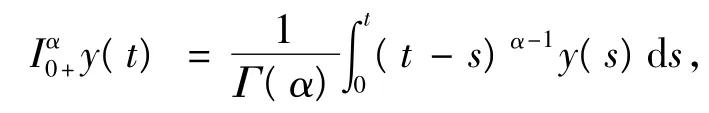
其中，α＞0，Γ(·)为Gamma函数.

定义2［1］连续函数y:(0，+∞)→R的α阶Riemann-Liouville分数阶导数为，

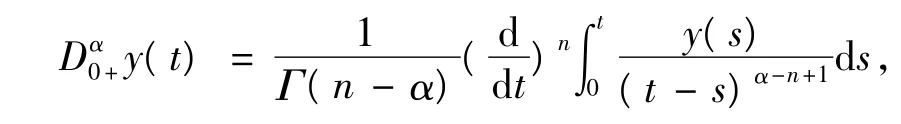
其中，α＞0，Γ(·)为Gamma函数，n=［α］+1.

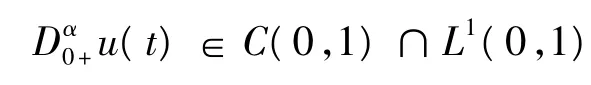
其中，N为大于或等于α的最小整数.

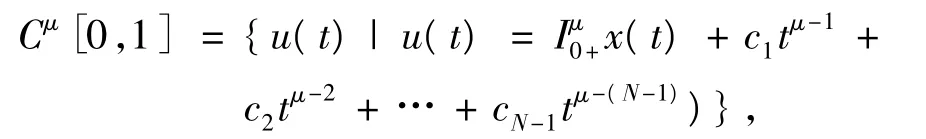
其中，x∈C［0，1］，ci∈R，i=1，2，…，N-1，其范数为，

易证得，Cμ［0，1］是Banach空间.

引理2［2］f⊂Cμ［0，1］是连续紧，当且仅当f一致有界且等度连续.

这里的一致有界是指存在M＞0，使得对任意u∈f有，

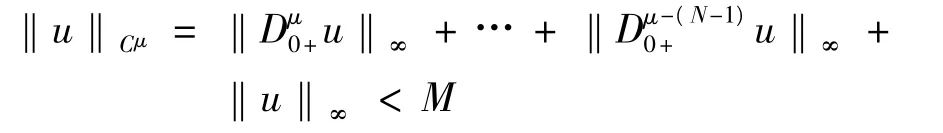
等度连续是只对∀ε＞0，∃δ＞0，使得，

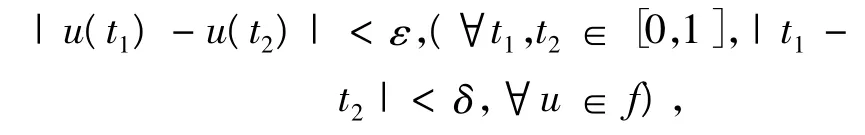
且，

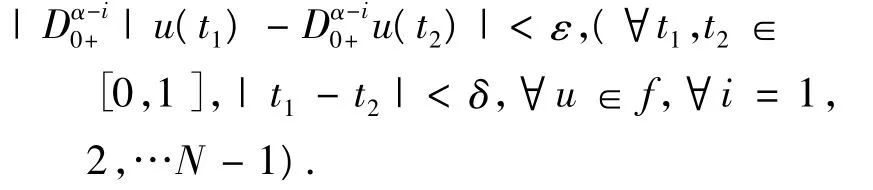
定理1［5］设Ω⊂Y是一个有界开集，L是一个指标为零的Fredholm算子，N是L-紧的，如果下面条件成立，

(1)Lx≠λNx，∀(x，λ)∈［domLKerL∩∂Ω］×［0，1］;

(2)Nx∉ImL，∀x∈Ker∩∂Ω;

(3)deg(JQN|KerL，KerL∩Ω，0)≠0，则方程，Lx =Nx，在domL∩Ω—中至少有一个解.

2 主要结果

令Z=L1［0，1］，范数为，‖y‖∫01|y(s)|ds，Y1=Cα-1［0，1］，Y2=Cβ-1［0，1］，由式(4)知，

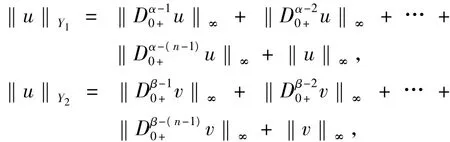
其中，Y=Y1×Y2是 Banach空间，‖(u，v)‖Y= max{‖u‖Y1，‖v‖Y2}，Z=Z1×Z1是Banach空间，‖(x，y)‖Z=max{‖x‖1，‖y‖1}.

定义L1是从domL1∩Y1到Z1的线性算子，

domL1={u∈Cα-1［0，1］|Dα0+u∈L1［0，1］，u满足式(2)}，L1u=Dα0+u，u∈domL1.

定义L2是从domL2∩Y2到Z1的线性算子，

domL2={v∈Cβ-1［0，1］|Dβ0+v∈L1［0，1］，v满足式(3)}，L2v=Dβ0+v，v∈domL2.

定义L是从domL∩Y到Z的线性算子，

domL={(u，v)∈Y|u∈domL1，v∈domL2}，L(u，v)=(L1u，L2v).

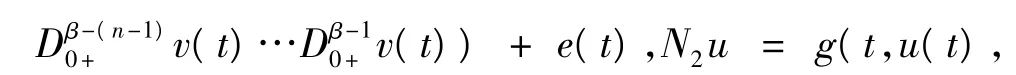
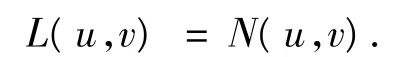
引理3 映射L:domL⊂Y→Z是一个指标为零的Fredholm算子.

证明 显然，KerL1={atα-1+btα-2|a，b∈R}≅R2，KerL2={ctβ-1+dtβ-2|c，d∈R}≅R2，KerL= {atα-1+btα-2，ctβ-1+dtβ-2|a，b，c，d∈R}≅R2×R2.

一方面，令(x，y)∈ ImL，则存在，(u，v)∈domL，使得，(x，y)=L(u，v)，即，u∈Y1，x=Dα0+u和v∈Y2，y=Dβ0+v，则由引理1可知，

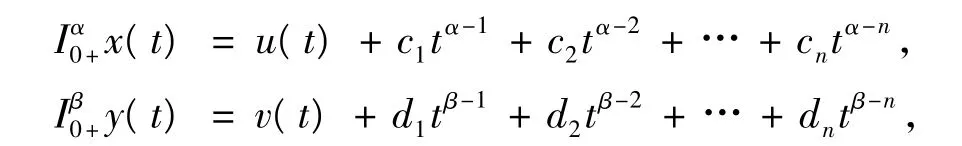
由边值条件知，c3=c4=… =cn=0，c1，c2是任意常数，x满足，

由边值条件知，d3=d4=… =dn=0，d1，d2是任意常数，y满足，

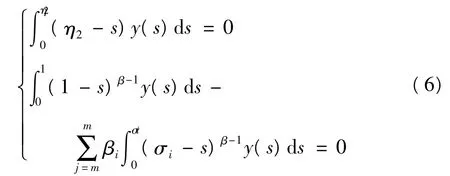
另一方面，假设(x，y)∈Z1分别满足式(5)、(6)，令，u(t)=Iα0+x(t)，v(t)=Iβ0+y(t)，那么，u∈domL1，Dα0+u(t) =x(t)和 v∈ domL2，Dβ0+v(t) = y(t)，即，(x，y)∈ImL.因此，可得到，ImL={(x，y)∈Z|x满足(5)，y满足(6)}.

考虑定义连续线性映射，Ai，Bi，Ti，Ri，Qi:Z1→Z1，i=1，2和Q:Z→Z，

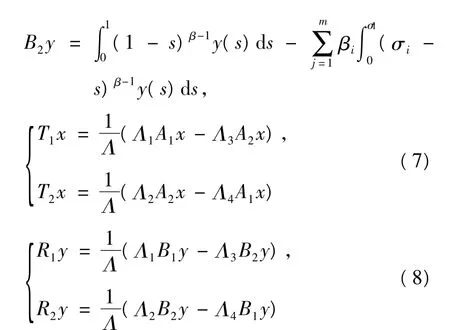
因为条件(C1)、(C2)成立，定义映射，

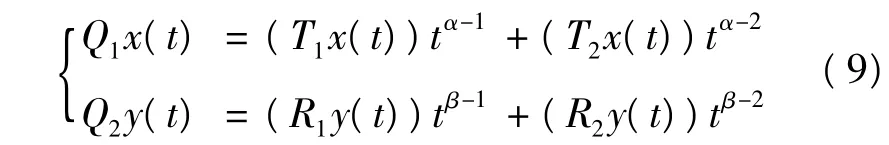
显然，dimImQ1=dimImQ2=2.

由条件(C1)、(C2)，注意到，

同理可得，

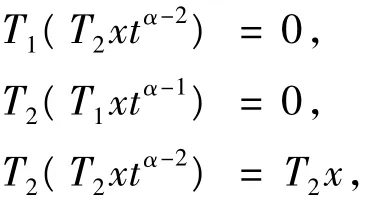
所以，对于x∈Z1，有，

即，Q1是连续线性投影算子.

同理可知，Q2也是连续线性投影算子.所以，Q(x，y)=(Q1x，Q2y)是一个连续线性投影算子.

注意到(x，y)∈ImL可推得，Q(x，y)=(Q1x，Q2y)=(0，0).反过来说，如果式子Q(x，y)=(0，0)成立，则有，

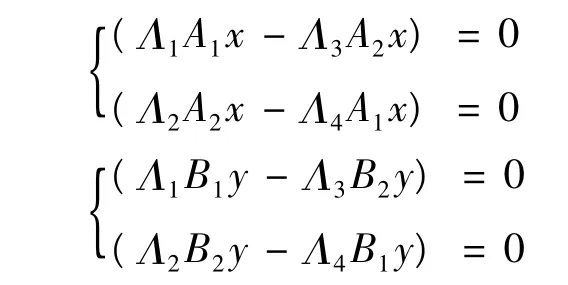
但是，

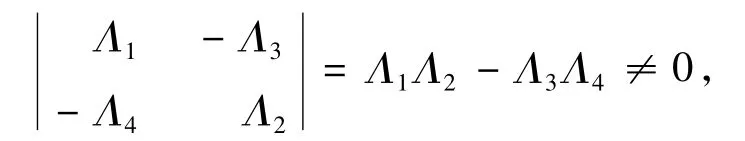
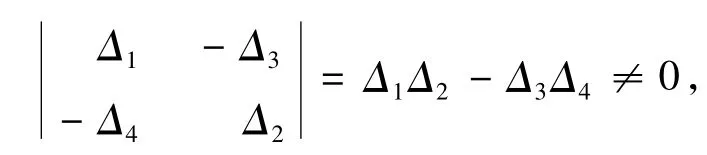
故一定有，Aix=Biy=0，i=1，2，即，(x，y)∈ImL，得到，KerQ=ImL.

令(x，y)∈Z，则，(x，y)=((x，y)-Q(x，y)) +Q(x，y)，使得，((x，y)-Q(x，y))∈KerQ=ImL，Q(x，y)∈ImQ成立.因此，Z=ImL+ImQ.再令(x，y)∈ImL∩ImQ，假设，(x，y)=(atα-1+btα-2，ctβ-1+dtβ-2)在［0，1］上不同时为0，因为(x，y)∈ImL，即x满足(5)，y满足(6)，可得到，a=b=c=d=0，矛盾，所以，ImL∩ ImQ={0，0}.即，Z=ImL⊕ImQ.现在，IndL=dimKerL-codimImL=0，所以，L:domL⊂Y→Z是一个指标为零的Fredholm算子.

定义，P1:Y1→Y1，P2:Y2→Y2，P:Y→Y，

注意到，P1，P2，P是连续线性投影算子.

显然，Y=kerL⊕kerP.

定义KP:ImL→domL∩KerP，KP(x，y)=(Iα0+x，

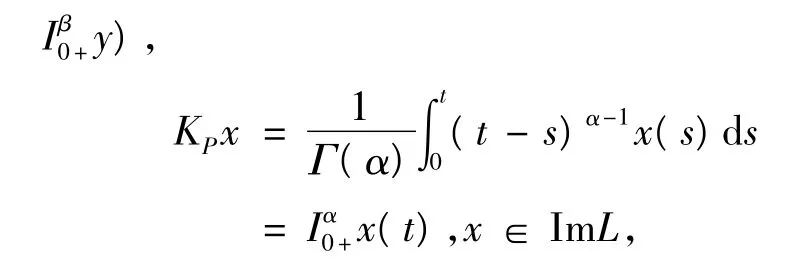
所以有，

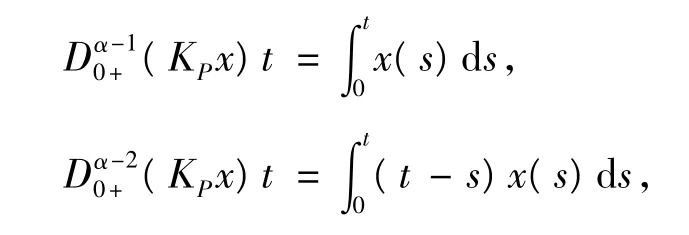
由此可知，

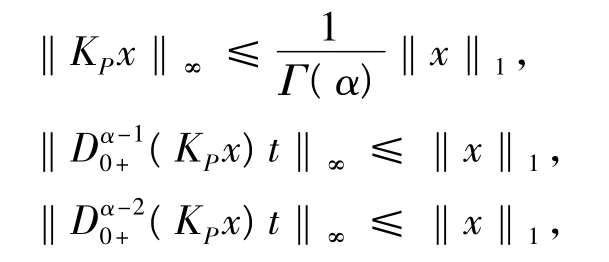
进一步可得，

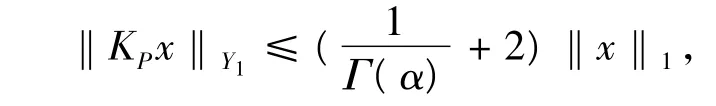
同理，

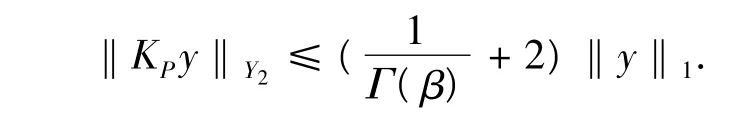
所以，

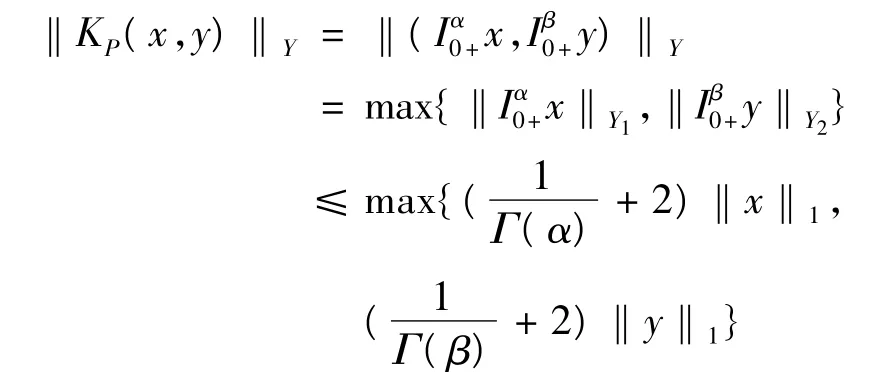
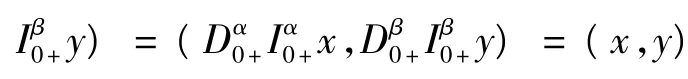
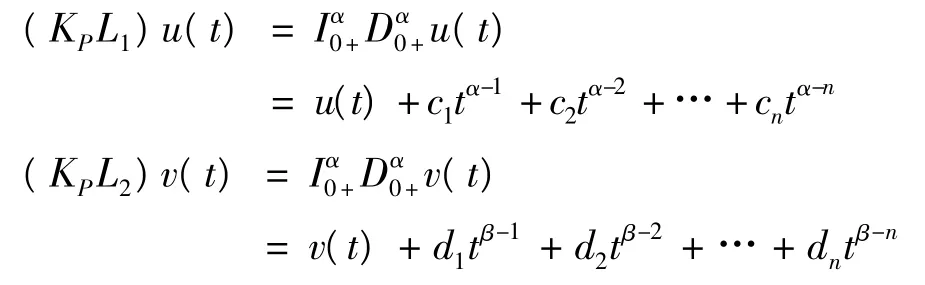
结合式(2)、(3)，可知，ci=0，di=0，i=1，…，n.即，(KPL)(u，v) = (u，v)，因此，KP=［L |domL∩KerP］-1.由式(7)、(8)、(9)可知，

结合引理2，可得到下面的引理.

引理4 KP(I-Q)N:Y→Y是全连续算子.设，

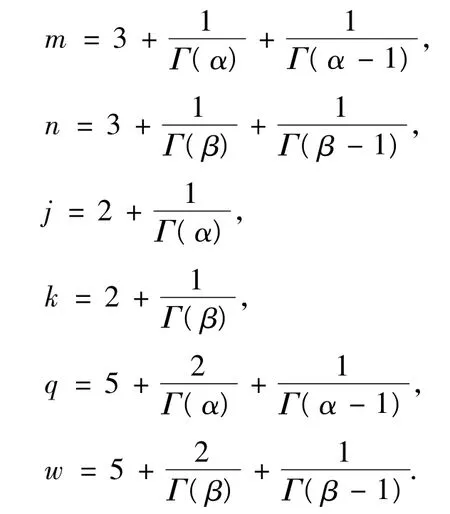
(A1) 存 在 函 数，a1(t)，b1(t)，…，bn-1(t)，c1(t)，r1(t)∈L1［0，1］，θ1∈［0，1］，使得对于(x，y1，…，yn-1)∈Rn，t∈［0，1］，有，

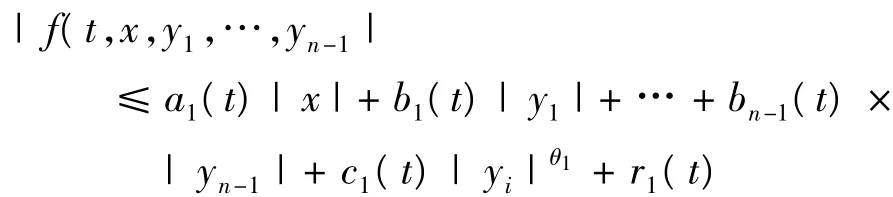
存在函数，a2(t)，d1(t)，…dn-1(t)，c2(t)，r2(t) ∈L1［0，1］，θ2∈［0，1］，使得对于(x，y1，…yn-1)∈Rn，t∈［0，1］，有，

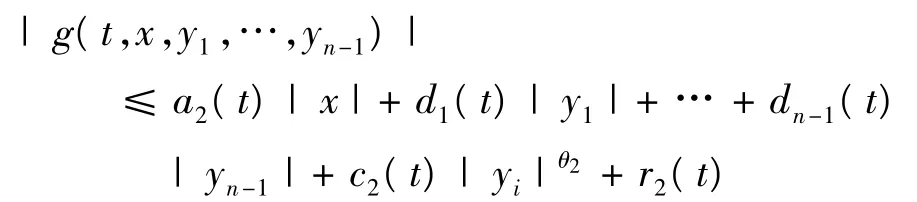
(A2)∃A＞0，使得对于(u，v)∈domLkerL，t∈ ［0，1］， 满 足，min{| D0α+-1u(t) |+ … +| D0α+-(n-1)u( t)|，D0β-+1v(t)|+…+|D0β-+(n-1)v(t)|} ＞A，有，

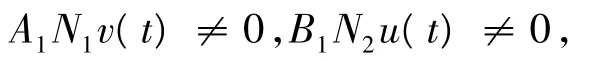
或，

(A3)∃A*＞0，使得对于a，b，c，d∈R满足，min{a2+b2，c2+d2}＞A*有，

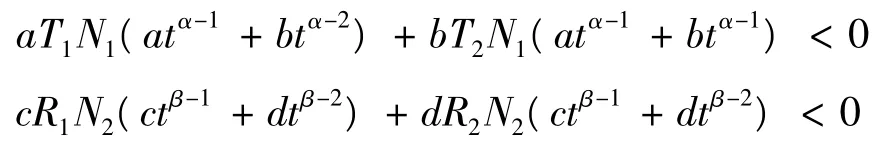
或，

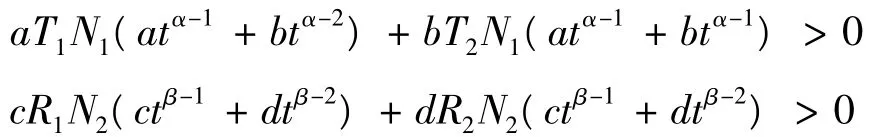
定理2 如果条件(C1)、(C2)和(A1)、(A2)、(A3)成立，并且

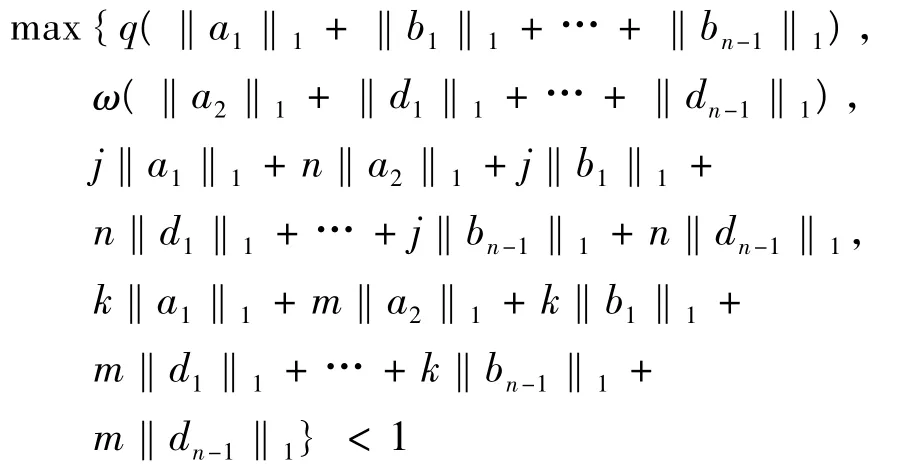
那么边值问题(1)、(2)、(3)至少有一个解.

证明 令Ω1={(u，v)∈domLKerL:L(u，v) =λN(u，v)，λ∈［0，1］}，对于(u，v)∈Ω1，有L(u，v)=λN(u，v)，因此λ≠0，N(u，v)∈ImL=KerQ，所以，对于t∈［0，1］，有QN(u，v)=(0，0).

由Q的定义，有Q1N1v(t)=Q2N2u(t)=0.据(A2)，存在t0，t1∈［0，1］，使得，

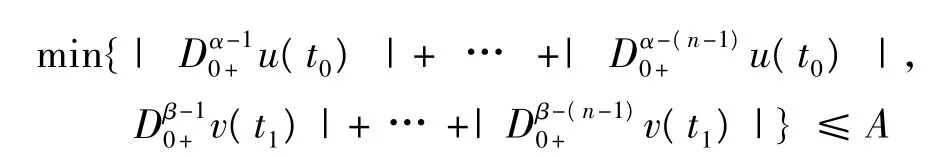
成立.

所以，

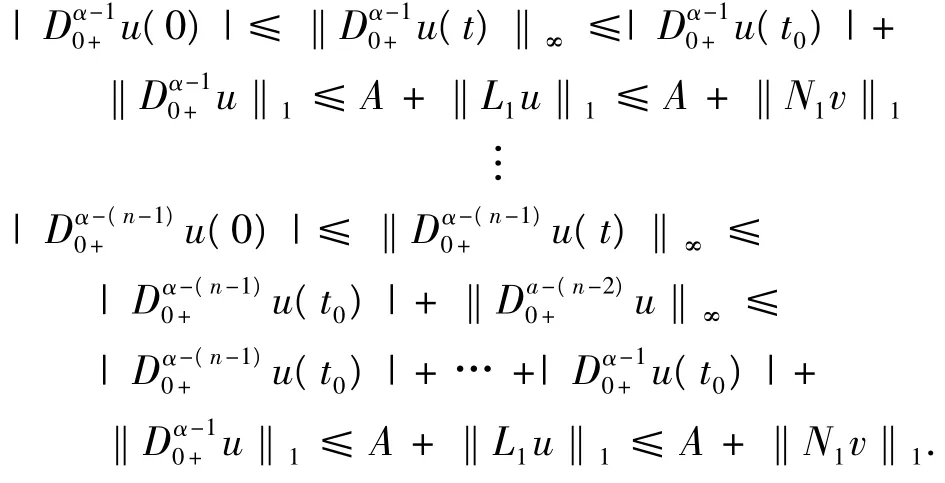
同理，

注意到，对于(u，v)∈Ω1，有(I-P)(u，v)∈domL∩KerP成立，那么，

所以有，

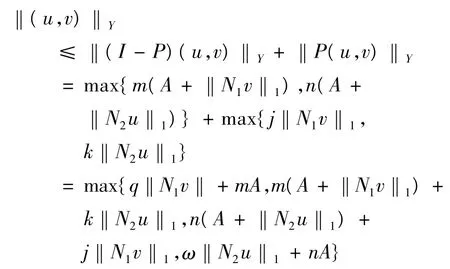
下面证明分成四部分.如果(A1)满足，

条件1.

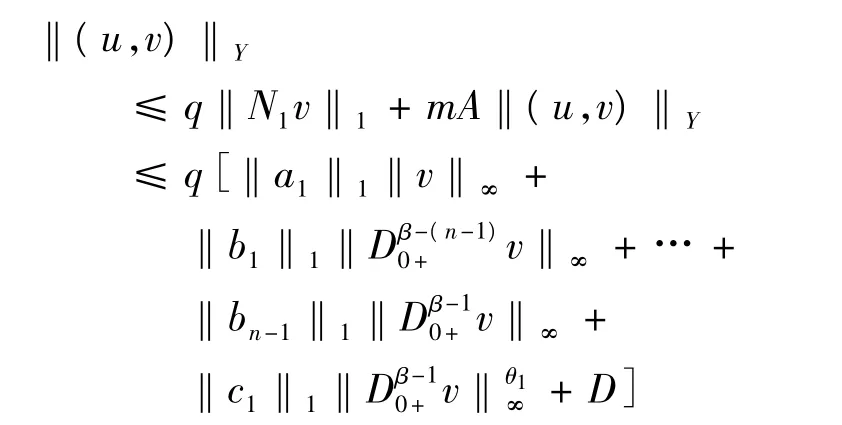
由于 ‖v‖∞，‖Dβ-(n-1)0+v‖∞，…，‖Dβ-10+v‖∞≤‖(u，v)‖Y，所以，

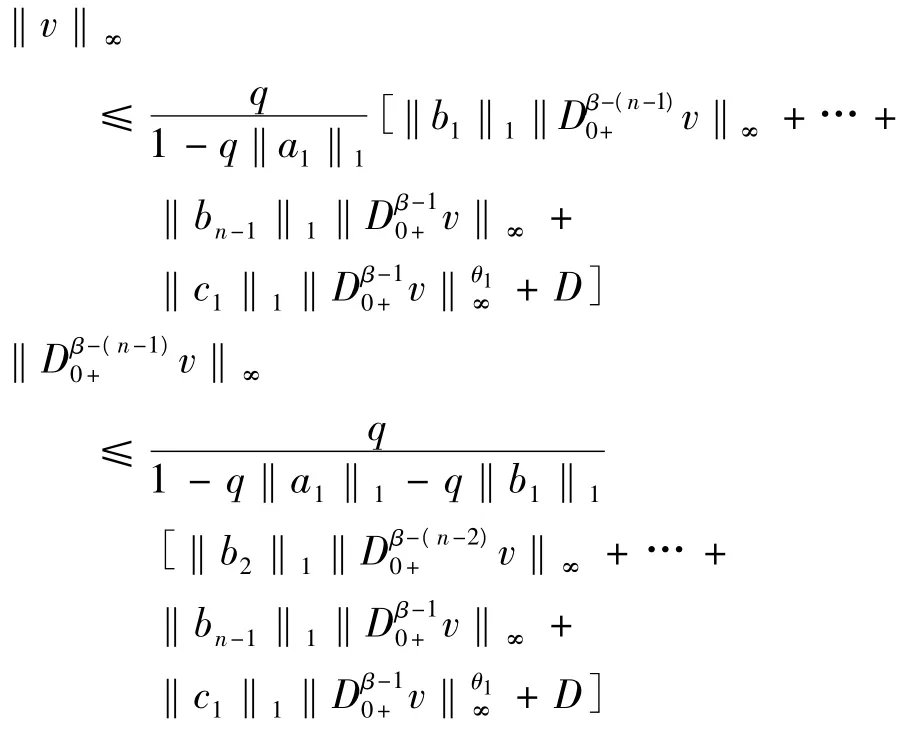
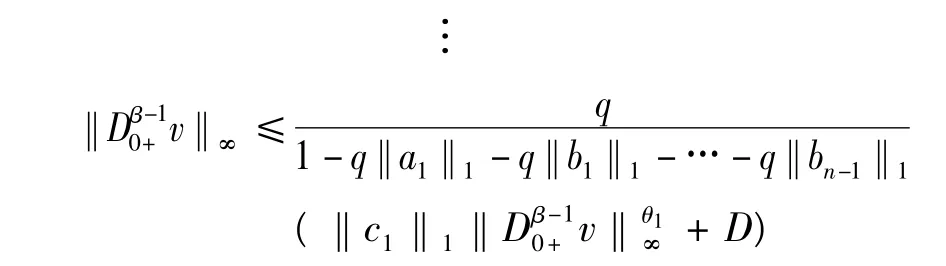
但是，θ1∈［0，1］和‖a1‖1+‖b1‖1+… +‖bn-1‖1≤，所以存在，M0，…，Mn-1＞0，使得，‖v‖∞≤ M0，‖D0β-+1v‖ ≤ M1，…，‖D0β+-(n-1)v‖ ≤Mn-1， 故 对 于， (u，v) ∈ Ω1，‖(u，v)‖Y= max{‖v‖∞，‖D0β+-1v‖∞，…，‖D0β-+(n-1)v‖∞} ≤max{M1，…，Mn-1}，即Ω1有界.

条件2.

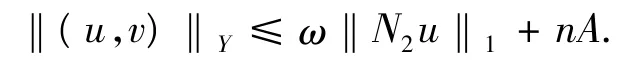
证明过程同条件1，其中，‖a2‖1+‖d1‖1+…

条件3.

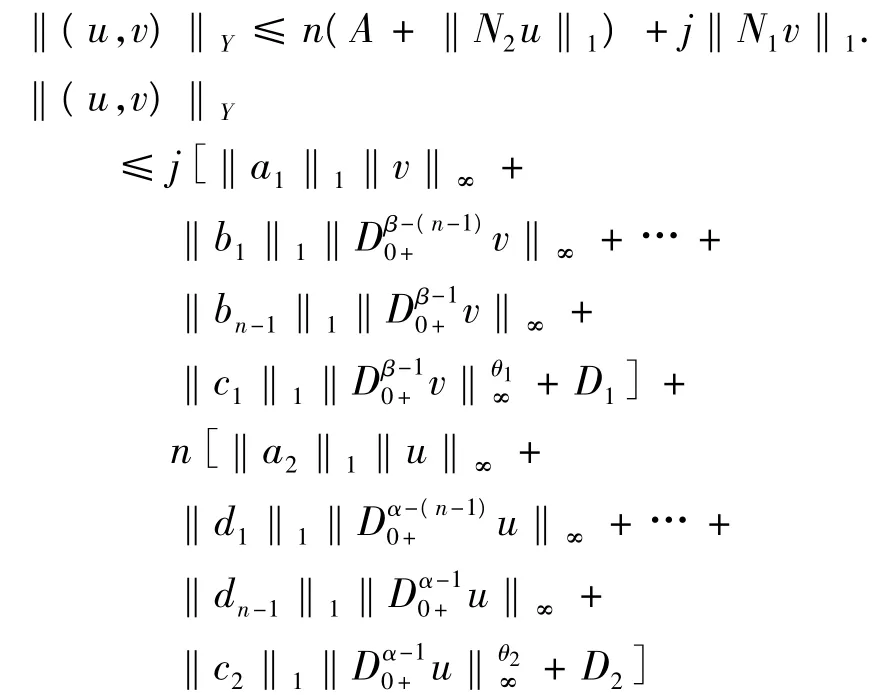
其中，D1=‖r1‖1+‖e‖1，D2=‖r2‖1+‖e‖1+A.

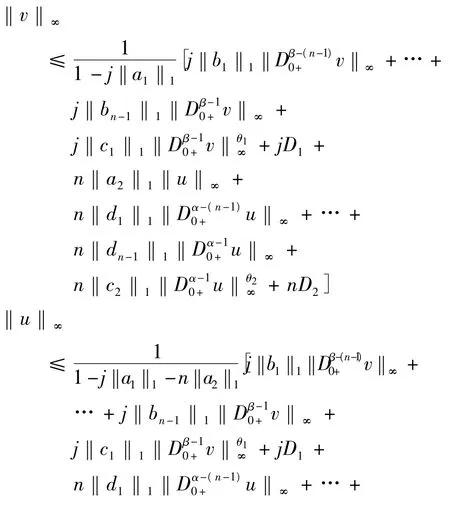
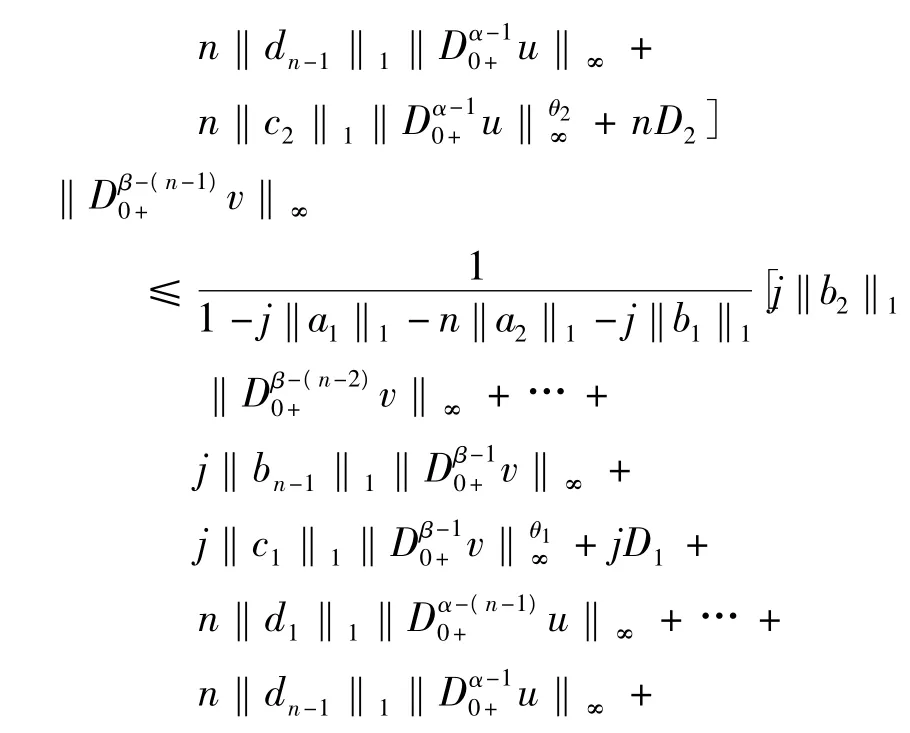
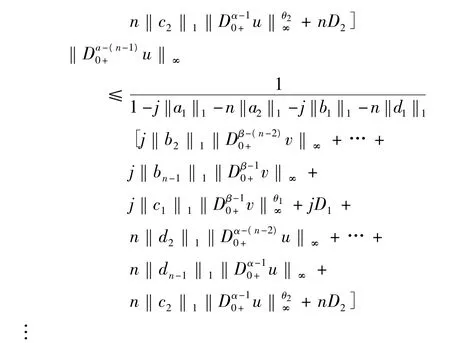
如果，j‖c1‖1Dβ-10+v‖θ1∞≤n‖c2‖1‖Dα-10+u‖θ2∞，有，

但是，θ2∈［0，1］和 j‖a1‖1+n‖a2‖1+ j‖b1‖1+n‖d1‖1+…+j‖bn-1‖1+n‖dn-1‖1＜1

所以存在，M0，…，Mn-1，M′0，…，M′n-1＞0，使得，

如果，j‖c1‖1‖Dβ-10+v‖θ1∞≥n‖c2‖1‖Dα-10+u‖θ2∞，同样可证明Ω1有界.

条件4.

证明过程同条件3，其中，k‖a1‖1+m‖a2‖1+ k‖b1‖1+m‖d1‖1+…+k‖bn-1‖1+m‖dn-1‖1

＜1.

令，Ω2={(u，v)∈KerL:N(u，v)∈ImL}，对于，(u，v)∈Ω2，(u，v)∈KerL={(u，v)∈domL| (atα-1+btα-2，ctβ-1+dtβ-2)，a，b，c，d∈ R，t∈［0，1］}和QN(u，v)=(0，0)，因此，

由(A3)，min{a2+b2，c2+d2}≤A*，即Ω2有界.

定义线性同构J:ImQ→KerL，

若(A3)第一部分成立，令，Ω3={(u，v)∈KerL:-λJ-1(u，v)+(1-λ)QN(u，v)=(0，0)，λ∈［0，1］}，对于任意，(u，v)=(atα-1+btα-2，ctβ-1+

如果λ=1，那么a=b=c=d=0;如果，min{a2+b2，c2+d2}＞A*，那么根据(A3)，

设Ω是Y中的有界开集，使得U3i=1Ω—i⊂Ω.根据引理4，映射KP(I-Q)N:Y→Y是紧的，因此，N在Ω—是L-紧的.根据上述论述，定理1中的(1)，(2)已满足，最后，我们将证明定理1的(3)满足，令，H((u，v)，λ)=±λJ(u，v)+(1-λ)JQN(u，v)，通过上面论述，可知，对于(u，v)∈∂Ω∩KerL，H((u，v)，λ)≠0.所以，

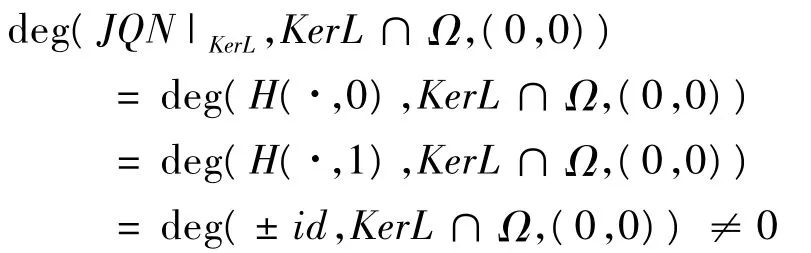
由定理1可知，L(u，v)=N(u，v)在domL∩Ω—上至少有一个解，即边值问题(1)、(2)、(3)在Y上至少有一个解.

得出矛盾，若(A3)的另一部分成立，

同样可得出矛盾.因此，可推知，

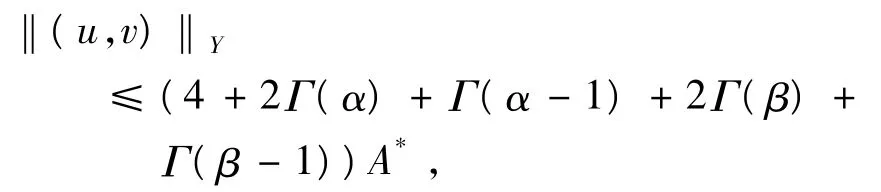
即Ω3有界.

［1］Bai Z B，Lu H S.Positive Solutions for Boundary Value Problem of Nonlinear Fractional Differential Equation［J］.Journal of Mathemalical Analysis and Applications，2005，311(2): 495-505.

［2］Zhang Y H，Bai Z B.Existence of Solutions for Nonlinear Fractional Three-point Boundary Value Problems at Resonance［J］.Journal of Applied Mathematics Computing，2011，36(1):417-440.

［3］Bai Z B，Zhang Y H.The Existence of Solutions for a Fractional Muti-point Boundary Value Problems［J］.Computers and Mathematics with Applications，2010，60(8):2364-2372.

［4］Zhang Y H，Bai Z B，Feng T T.Existence Results for a Coupled System of Nonlinear Fractional Three-point Boundary Value Problems at Resonance［J］.Computers and Mathematics with Applications，2011，61(4):1032-1047.

［5］Wang G，Liu W B，Zhu S N，et al.Existence Results for a Coupled System of Nonlinear Fractional 2m-point Boundary Value Problems at Resonance［J］.Advances in Difference E-quations，2011，44(1):1-17.

［6］郭大钧，孙经先，刘兆理.非线性常微分方程泛函方法［M］.济南:山东科学技术出版社，2006.

［7］王刚，朱思念.一类分数阶多点边值共振问题解的存在性［J］.淮阴师范学院学报(自然科学)，2011，10(3):193-200.

［8］Bai Z B.On Solutions of some Fractional M-point Boundary Value Problems at Resonance［J］.Electronic Journal of Qualitative Theory of Differential Equations，2010，37(1):1-15.

［9］Su X.Boundary Value Problem for a Coupled System of Nonlinear Fractional Differential Equations［J］.Applied Mathematics Letters，2009，22(1):64-69.