模糊神经网络在冷连轧厚度控制中的应用

薛 薇，吴青华

(天津科技大学电子信息与自动化学院，天津 300222)

模糊神经网络在冷连轧厚度控制中的应用

薛 薇，吴青华

(天津科技大学电子信息与自动化学院，天津 300222)

由于冷连轧厚度控制系统具有非线性、大时滞的特点，在冷连轧厚度的常规 PID控制中，PID控制器的参数往往针对某一种情况进行整定，很难控制冷连轧厚度始终处于一个好的状态.为此，在分析了厚度控制原理的基础上，设计了用一个2-5-1结构的BP网络实现的模糊神经网络控制器(FNNC)，并将该FNNC控制器与积分作用相结合构成一个FNNC-I控制器.仿真结果表明，该FNNC-I控制器提高了系统的动态和稳态性能、抗干扰性以及鲁棒性，其控制效果优于常规PID控制器.

冷连轧；厚度控制；模糊神经网络；PID

在冷轧过程中，自动厚度控制(AGC)是冷连轧机控制系统的重要组成部分，其性能的优劣直接影响产品的质量，同时还会影响板型控制的精度.因此，自动厚度控制对提高产品的厚度和板形精度有重要的意义.

早期采用的是直接测量厚度的反馈式自动厚度控制[1]，通常采用常规PID控制.常规PID控制器原理简单、设计方便，在工业控制中被广泛应用，但控制器对系统模型的精确性依赖较强，对于非线性、时变且受随机干扰的系统，一般难以获得较好的控制性能[2].虽然冷连轧厚度的测量仪器(比如 KELK 公司生产的张力测量仪)测出的精度较高，经二次仪表处理后实时性也较好，但是测量点与执行器的工作点存在着较大距离，因此系统存在较大的滞后；而且在执行器执行时，又存在液压系统的响应滞后.按照常规PID控制方式，控制系统响应不及时，必然导致系统超调量大，调节时间长，控制效果不佳；在实际应用中很难获得高精度的厚度控制数学模型，这也使得依赖高精度数学模型的 PID控制在厚度控制上不能发挥其优势.换言之，冷连轧机是复杂的机、电、液多变量耦合的大滞后的物理系统，在实际轧制过程中影响机架厚度的工艺参数很多，厚度的变化又对其他工艺参数产生相互影响.若采用PID控制，很难达到厚度控制系统的要求，因此越来越多的研究人员开始关注智能方法在厚度控制中的应用[3].一种做法是采用Smith预估器进行补偿[4–5]，但Smith预估器的抗干扰能力较差，且对数学模型的误差十分敏感，模型失匹会使得系统稳定性和鲁棒性变差.而模糊神经网络控制器由于具有良好抗干扰性和鲁棒性，在许多工业过程中得到了广泛的应用[6–8].

本文设计一个 3层结构的 BP网络实现的模糊神经网络控制器(FNNC)，该模糊神经网络控制器结构及算法简单、实现方便.为了提高控制系统的稳态性能，在此基础上将 FNNC控制器与积分作用相结合，构成了一个 FNNC-I控制器.该控制器在厚度控制中取得了较好的控制效果.

1 厚度控制系统模型

以酸洗五连轧联合机组的轧机为例，对辊缝内环进行 PID控制，并考虑测厚仪滞后的影响，可以得到整个厚度环被控对象的传递函数[1]为

图1 轧机示意图Fig.1 Schematic diagram of mill

2 模糊神经网络控制系统

2.1 FNNC结构与算法

2.1.1 FNNC的结构

本文采用的模糊神经网络控制器结构框图如图2所示.

图2 FNNC的原理结构图Fig.2 Structrue diagram of FNNC principle

为了更好地提高系统的稳态性能，在 FNNC基础上再并联一个积分控制环节，构成一个 FNNC-I控制器.图中，ke为误差量化因子，kc为误差变化量化因子，ku为控制器输出的比例因子，ki为积分环节放大系数.

模糊系统善于直接表示逻辑，适于直接表示知识；神经网络长于学习，通过数据隐含表达知识.对于模糊神经网络控制器，如何把模糊逻辑推理与神经网络技术相结合，采用什么样的神经网络结构来实现模糊逻辑控制作用，大多数学者提出的网络结构都是与模糊逻辑推理的前后件相匹配的结构，这样的网络结构较为复杂，一般为 4层或 5层网络，其算法复杂、训练及学习过程较长，不便于进行实时控制和应用开发[10].

本文采用的模糊逻辑和神经网络相结合的方式是用神经网络学习并记忆模糊规则的控制.即通过一组神经元不同程度的兴奋表达一个抽象的概念值，由此将抽象的经验规则转化成神经网络的输入输出样本，通过神经网络学习并记忆这些样本，控制器以联想记忆方式使用这些经验，在一定意义上与人的联想记忆思维方式接近.神经网络中应用最广的是多层前向网络，多层前向网络应用于具体实时控制问题时，必须有一个训练网络权值的算法，应用最广的是BP算法，这种算法思路简洁明了，具有自适应、自学习、自组织功能.考虑到 BP网络已经成功地应用于多种控制系统，并且其结构简单、易于实现，选用 3层的BP网络作为模糊神经网络控制器[11]，其结构如图3所示.

图3 BP网络结构图Fig.3 Structrue diagram of BP network

图3是一个2-5-1结构的BP网络，输入层节点有 2个，分别是误差E和误差变化EC；中间层节点有 5个，这一层的节点数目不是固定不变的，可以根据实际情况进行调整，一般为 5个左右；输出层节点只有一个，即控制量U.

2.1.2 FNNC算法

BP 网络采用如下控制算法[11–12]：

式中：t为训练次数；n0(t)为输入样本函数；n(t)为网络实际输出函数.学习算法采用带有阻尼项的BP算法，即

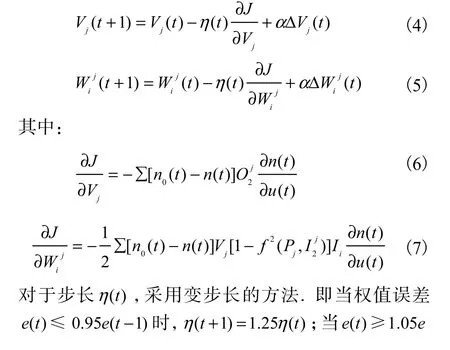
2.2 初始权值的确定

厚度控制中的神经网络初始值可以由模糊控制表作为学习样本离线学习得到.这里选用带有自调整因子的模糊控制器的输入、输出构成模糊控制表.即

经过样本学习后得到的初始权值组成的模糊神经网络控制器，在控制初期就已经被赋予了人的操作经验.

3 仿真研究

3.1 PID稳定域的确定与参数整定

为了更好地对 PID控制器进行参数整定，首先使用确定 PID参数稳定域的图解法[13]，在参数空间中，用拟多项式(Quasi-Polynomial)稳定的一个图解准则，直接绘出PID参数的稳定域.然后在所确定的稳定域中选择一组合适的PID参数.

按照文献[13]给出的图解法，在确定kp＝0.025时，绘制出kd，ki的稳定域如图 4所示.图 4中的阴影区为kd、ki参数稳定区.在稳定域范围内，kp＝0.025，kd＝0.01，ki＝0.45时系统响应曲线最佳，因此，选取这组参数作为PID控制器参数.

图4 kp=0.025时，kd和ki的稳定域Fig.4 Stabilizing regions ofkdandkiwhenkp=0.025

3.2 模糊神经网络与传统PID的仿真结果

PID控制器的参数整定为：kp＝0.025，kd＝0.01，ki＝0.45；FNNC-I控制器的参数按经验整定为：ke＝5，kc＝0.01，ku＝1，ki＝0.42.

不加任何干扰，在单位阶跃信号的作用下，两种控制器的仿真结果见图 5.在单位阶跃信号的作用下，t=15s时，加相同幅值为 0.25的阶跃扰动，两种控制器的仿真结果见图6.

图5 无干扰时的仿真结果对比Fig.5 Comparison of simulation when noninterference

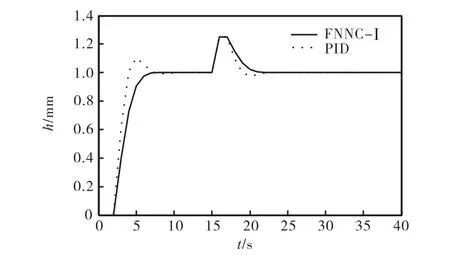
图6 加干扰时的仿真结果对比Fig.6 Comparison of simulation when interference

由图5可以看出，FNNC-I没有超调，而 PID控制器的超调明显，达到12%.图6中，在有干扰的情况下，PID 的抗干扰能力不如 FNNC-I，PID 控制存在负超调.

由于冷轧机组轧制速度是可变的，这样就造成系统控制对象的滞后时间不一样.当滞后时间τ=2s时，PID控制器和 FNNC-I控制器的响应曲线见图7.滞后时间τ=3s时，PID控制器和FNNC-I控制器的响应曲线见图8.

在图7中的仿真结果中，PID控制器最大超调为38%，而此时 FNNC-I没有超调.在图 8中的仿真结果中，PID控制器最大超调为63%，FNNC的超调只有1%.随着延时时间的加长，PID控制器的超调明显变大，调节时间变长.由此可以看出，在系统模型参数改变时，FNNC-I控制系统比传统的PID控制系统具有更好的动态、稳态性能，响应速度快且超调小.这说明模糊神经网络控制对被控对象精确数目模型的依赖性明显小于传统的PID控制.

图7 延时时间τ=2s时的仿真结果对比Fig.7 Comparison of simulation whenτ=2s

图8 延时时间τ=3s时的仿真结果对比Fig.8 Comparison of simulation when τ=3s

4 结 语

本文针对冷连轧AGC系统对象存在较大的时滞以及过程模型参数变化的特点，提出一种带积分环节的模糊神经网络控制器(FNNC-I)的解决方案.仿真验证说明，该模糊神经网络控制策略用于轧机的厚度控制是可行的，能稳定控制轧制厚度，并有较好的控制效果.

［1］孙一康. 带钢冷连轧计算机控制[M]. 北京：冶金工业出版社，2002.

［2］赵庆海，贾中华. 模糊自适应 PID 控制在张力控制中的应用[J]. 包装工程，2008，29(1)：87–89.

［3］贾春玉. 基于模糊神经网络推理的智能厚度控制[J].钢铁研究学报，2001，13(2)：50–53.

［4］李伯群. 热连轧厚度综合控制技术的应用研究[D]. 北京：北京科技大学，2006.

［5］陈连贵，杨卫东，杨斌虎. 基于鲁棒二自由度增益自适应 Smith预估器的冷轧厚度计型 AGC[J]. 北京科技大学学报，2007，29(6)：632–635.

［6］牛培峰，高龙，陈贵林，等. 模糊神经网络自适应控制在循环流化床锅炉燃烧控制系统中的应用研究[J]. 燕山大学学报，2011，35(4)：328–333，350.

［7］周水英，蔡杰，钟汉如. 基于模糊神经网络的气流雾化染色机温度控制[J]. 制造业自动化，2011，33(17)：116–119.

［8］葛超，孙艳彬，张景春，等. 基于模糊神经网络的锅炉蒸汽压力控制系统[J]. 可编程控制器与工厂自动化，2010(1)：87–89.

［9］李仲德，杨卫东. 冷连轧 AGC系统的自适应Smith广义预测控制[J]. 信息与控制，2009，38(5)：575–579.

［10］赵振宇，徐用懋. 模糊理论和神经网络的基础与应用[M]. 北京：清华大学出版社，1996.

［11］薛薇，齐国元，李力，等. pH过程的FNNC–PI控制研究[J]. 仪器仪表学报，2004，25(6)：721–724，733.

［12］Xue Wei，Guo Yanling. Fuzzy neural network control in main steam temperature system[J]. ICIC Express Letters，2009，3(3)：409–414.

［13］王德进. 一种确定 PID参数稳定域的图解法[J]. 控制与决策，2007，22(6)：663–666.

Fuzzy Neural Network on the Application in Thickness Control of Tandem Cold Mill

XUE Wei，WU Qinghua
(College of Electronic Information and Automation，Tianjin University of Science & Technology，Tianjin 300222，China)

There are nonlinear，large time delay characteristics of tandem cold mill thickness control，so it is difficult to keep thickness within a small tolerance using PID controller，whose parameters are set only for one stable situation. Based on the analysis of thickness control theory，a fuzzy neural network controller(FNNC)with simple structure was designed，which was realized by a BP network with 2-5-1 structure. On the basis of this controller，anintergral action was added to constitute FNNC-I controller. Simulation results show that the dynamic，static，anti-interference performance and the robusness of the system were all improved by this FNNC-I controller，so it is better than the conventional PID controller.

tandem cold mill；thickness control；fuzzy neural network；PID

TG335.5

A

1672-6510(2012)02-0049-04

2011–11–14；

2012–01–06

国家自然科学基金资助项目(60874028)

薛 薇（1963—），女，河北河间人，副教授，xuewei@tust.edu.cn.

常涛