复指数函数的定义问题

孙小康，徐松金

（ 铜仁学院 数学与计算机科学系，贵州 铜仁 554300 ）

复指数函数的定义问题

孙小康，徐松金

（ 铜仁学院 数学与计算机科学系，贵州 铜仁 554300 ）

对实数域中指数函数的定义在复数域上的推广及欧拉公式与复指数函数的关系进行了探讨。

欧拉公式； 复指数函数； 乘法运算

1.引言

复变函数论里的欧拉公式：eix= c osx+is inx，e是自然对数的底，i是虚数单位。它将三角函数的定义域扩大到复数域，建立了三角函数和指数函数的关系，在复变函数论里占有非常重要的地位。将公式里的x换成 −x，得到：e−ix= c osx−is inx，然后采用两式相加减的方法得到：

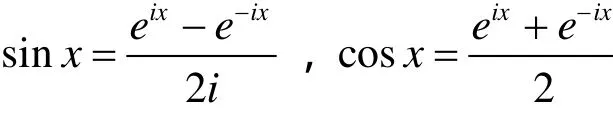
这两个也叫做欧拉公式。将eix= c osx+is inx中的x取作 就得到：eiπ+1 = 0 。这个恒等式也叫做欧拉公式，它是数学里最令人着迷的一个公式，它将数学里最重要的几个数联系到了一起，两个超越数：自然对数的底e、圆周率 ，两个单位：虚数单位i和自然数的单位 1，以及数学里常见的 0。复变函数教学中常碰到下面这些问题：欧拉公式是怎么得来的，为什么这样定义复指数函数与三角函数呢？复变函数的教材很多但是都没有详细地说明这个问题。本文对这些问题进行了讨论。

2.如何在复数域上定义指数函数

为了使负数开平方有意义，需要再一次扩大数域，于是，就引入了虚数，使实数域扩大到复数域。如何建立复数理论，首先要引入运算法则，然后将初等函数等这些最基本的概念推广到复数域。给出两个复数z1=x1+iy1和z2=x2+iy2，其加法、减法的定义为实部与虚部分别相加减。乘法如何定义呢？给出复数的四则运算之后如何进一步进行处理？如何将导数、微分的概念推广到复变函数上来？如何将实数域上熟知的初等函数推广到复数域上来？

解析函数是复变函数研究的主要对象。它是一类具有某种特性的可微函数。函数成为解析函数的必要条件是满足柯西—黎曼条件，即如果是解析函数，则必须有

3.结论

[1]钟玉泉.复变函数论（第3版）[M].北京：高等教育出版社，2004.

[2]宛秀白.关于复指数函数定义的讨论[J].廊坊师专学报，1995，（4）.

[3]阿尔福斯.复分析[M].上海：上海科学技术出版社，1984.

The Definition of the Index Function in Complex Variables

SUN Xiao-kang, XU Song-jin
( Department of Mathematics and Computer Science, Tongren University, Tongren, Guizhou 554300,China )

In this paper, we discuss how to extend the definition of index function in field of real numbers to the field of complex numbers and discuss the relationship between Euler formula and complex index function.

Euler formula; Index function; multiplication

（责任编辑 毛志）

O174.5

A

1673-9639 (2012) 02-0141-03

2011-11-18

本文系铜仁学院校级课题（课题批准号：TR052）成果。

孙小康（1982-），女，湖南邵阳人，硕士，讲师，研究方向：基础数学、函数论。