基于神经网络的近震与远震识别*

曲均浩，刘希强，吴丹彤，张 芹，于 澄，穆 娟，苗庆杰

(山东省地震局，山东济南250014)

基于神经网络的近震与远震识别*

曲均浩，刘希强，吴丹彤，张 芹，于 澄，穆 娟，苗庆杰

(山东省地震局，山东济南250014)

选用P波震相附近的地震波作为研究对象，对近震和远震特征信息进行探讨。选取初至P波主周期作为神经网络输入元，P波到达后2～6 s作为地震波时间窗，选择正确的网络结构和参数，搜集大量的地震样本数据进行训练，实现对近震和远震地震事件的非线性系统识别。结果表明:在样本训练区间检验数据的预测结果置信度达到100%;在非样本区间也能迅速收敛到标识符0或1附近。近震样本信号最大周期为0.25 s，而置信度达到80%以上的预测区间几乎接近0.35 s;远震样本信号最小周期为0.9 s，而置信度达到80%以上的预测区间达到0.5 s，表明模型建立得当，具有良好的泛化能力。

BP神经网络;近震;远震;震相识别

0 引言

目前识别地震震相主要依靠地震分析人员人工交互处理。地震发生后能够快速准确、稳定可靠地测定地震三要素，使得速报的平均时间为10 min，是地震速报速度方面一个质的飞跃。在测震台网实时处理系统中，自动定位是一个重要的组成部分 (赵仲和，2005)，而近震和远震的识别则是自动定位的关键技术之一。在自动定位系统中，如果不能很好地识别近震与远震，则会获取错误的震相，导致将远震错误定位在本区域附近，发布错误地震参数。

近震与远震的定义是以震中距为判断标准的。地震波传播过程中，由于地壳介质、传播距离的不同导致地震波衰减后震相特征信息存在差异。分析人员能够根据地震波的振幅、周期、震中距、持续时间等特征信息识别出近震与远震，但是计算机必须掌握地震波量化的指标才能准确地识别近震与远震。

神经网络的应用已经渗透到各个领域并在智能控制、模式识别、计算机视觉、自适应滤波和信号处理等方面取得了进展。近年来神经网络理论已经被逐步用来对地震信号进行分析和处理(Coforth，Herin，1981;王娟等，2004;蔡煜东等，1994;穆星，2005;Jin，Ta-Liang，1988)。

1 BP神经网络

BP(Back Propagation)网络是1986年由以Rumelhart和McCelland为首的科学家小组提出的，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入—输出模式映射关系，而无需提前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input layer)、隐层 (hide layer)和输出层 (output layer)(图1)。

确定神经网络的结构和权系数来描述给定映射或逼近一个未知映射，只能通过学习方式得到满足要求的网络模型。对确定的网络结构，寻找一组满足要求的权系数，使给定误差函数最小。设计多层前馈网络时，主要侧重试验和探讨多种模型方案，在实验中不断改进，直到选取出一个满意方案为止，可按下列步骤进行:对任何实际问题先都只选用一个隐层，使用很少的隐层节点数，不断增加隐层节点数，直到获得满意性能为止;再采用2个隐层重复上述过程。训练过程实际上是根据目标值与网络输出值之间误差的大小反复调整权值和阈值，直到此误差达到预定值为止。

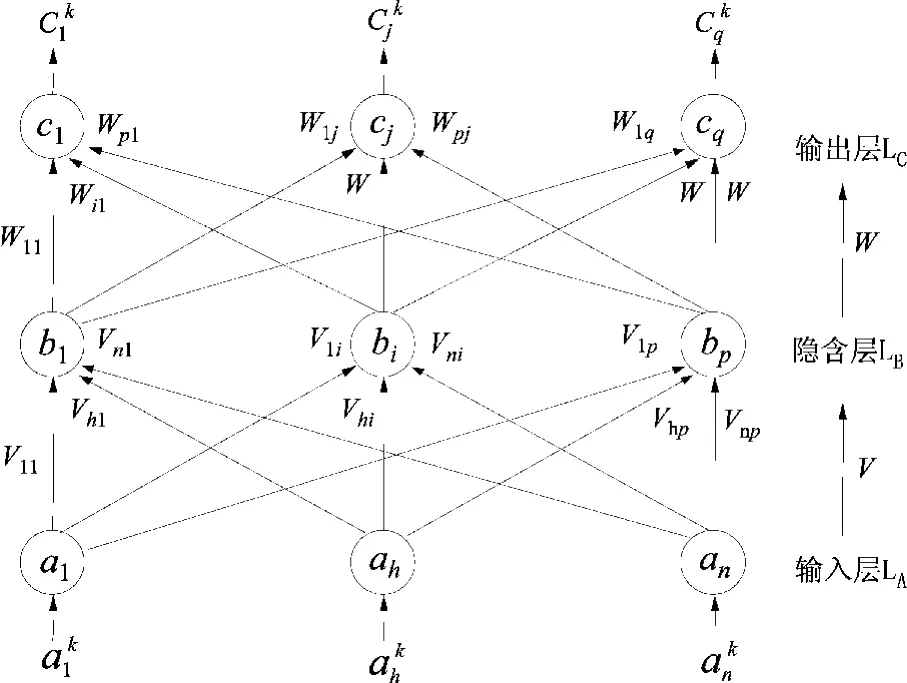
图1 基本BP网络的拓扑结构Fig.1 Topology structure of basic BP network

2 判别信息探讨

近震是指震中距小于1 000 km的地震，但本文讨论的近震更加接近于地方震 (震中距小于100 km的地震)。一般而言，地震远近的判断主要依据横波与初至波间的时间差、面波最大振幅与初至波之间的时间差、整个事件的振动持续时间等，或利用纵波、横波、面波之间的关系进行判断。地方震直达纵、横波之间的时间差小于13 s，振动持续时间通常为1～2 min(据J-B走时表)。近震首波、横波之间的时间差小于1分43秒，振动持续时间通常在3～5 min(据中国地区近震走时表)。远震面波的最大振幅与初至波之间的到时差小于45 min，地幔折射纵横波之间的时间差小于11分52秒，振动持续时间通常小于1.5 h(据震相走时便查表)(中国地震局监测预报司，2007)。上述近震与远震的识别依据无法满足自动定位系统的需求，区域地震自动定位系统识别近震与远震主要依靠初至P波到达后几秒内的特征信息进行判断，增加了判断的难度。

体现初至P波特征的信息有振幅、周期、到时差、视出射角等。不同台站P波的到时差会根据震中与台站的相对位置、震中距的大小而有所差异，无法准确判别近震与远震。近震与远震的初至P波振幅与地震震级有极其密切的关系，也不能作为近震与远震的判别依据 (通过震相实例表1可见，同一分量近震和远震幅值没有必然差别)。在震源深度相同的情况下，根据地震波射线理论，视出射角会随着震中距的增大逐渐减小，能够在一定程度上体现近震与远震的区别。在地震波的周期方面，一般认为近震的卓越频率较高，能量集中在高频段;远震的卓越频率较低，能量集中在低频段，因此初至P波的主周期可以作为近震与远震的判据之一。

2.1 视出射角

视出射角是地动位移矢量与地表面的夹角，由于地震波在地面上形成了反射波，所以视出射角不等于入射波的真出射角，可根据记录到的地面位移垂直分量和水平分量的比值确定视出射角。以观测点为坐标原点，规定正东、正北和垂直地表向上分别为x轴、y轴和z轴的方向。地震仪在t时刻记录到地震体波的位移可表示为

其中，ux(t)，uy(t)和uz(t)分别是3个分向的记录波形;ux(t)是径向波形;e和φ分别是初至波的视出射角和台站方位角。

地震波的3个分向位移记录波形及其对时间t的一阶和二阶导数可写成:

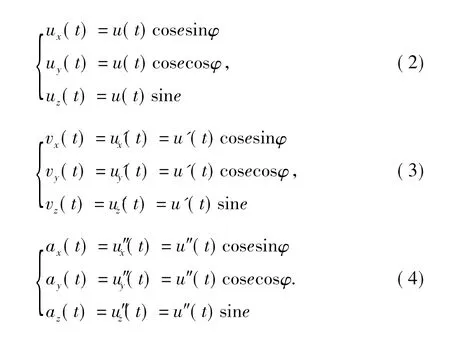
式(3)和式(4)分别表示地震波的速度记录和加速度记录。一般在微震记录时采用的是地面运动速度记录，而在强震记录时采用的是地面运动加速度记录。视出射角的计算公式为

根据P波的质点运动方向，在t时刻质点的位移、速度和加速度向量是平行的，所以无论是用哪种记录资料都可以直接计算视出射角。把 (2)、(3)、(4)式代入 (5)式，则有:

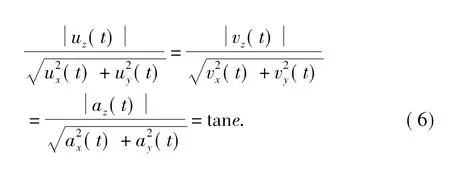
由式 (6)可知，在时间域计算地震初至波的视出射角时，无论使用何种记录资料 (位移、速度和加速度)都可直接计算，无需把速度和加速度记录转为位移记录再求出视出射角 (何斌等，2010)。

目前，山东测震台网观测台站全部采用速度型记录仪，其实际获取的数据并不是理想化的波形数据，还存在机械干扰、脉冲等复杂情况。这种周期不定、存在干扰的波形数据难以直接进行计算机化操作，有必要对数据进行预处理。本文主要采用等波纹切比雪夫逼近方法来实现最大误差最小化的滤波器设计 (Cichowicz，1993;Allen，1978)，以获得唯一的最佳解。图2为郯城台垂直向原始波形及预处理后获得的波形。从图中可以看出经过波形预处理后的事件波形震相非常清晰，有效剔除了低频背景噪声。

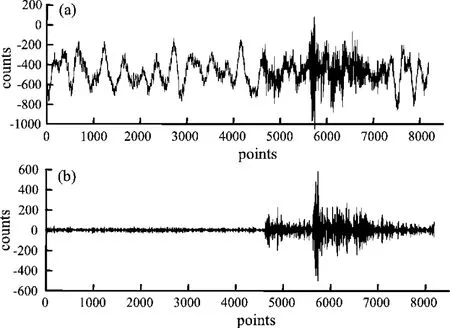
图2 郯城台垂直向原始波形(a)及处理后波形(b)Fig.2 Vertical original waveform(a)recorded in Tancheng Station and its waveform after pretreatment(b)

表1 近震与远震视出射角对比Tab.1 Apparent emergence angle comparison between near and distant earthquakes

以检测到地震波初至波到时为起点，计算其视出射角，由表1可以看出，远震的视出射角并不一定比近震的小。对于同一个地方震，在一定震中距范围内，随着震中距的增大，视出射角逐渐变小。而对于远震，初至震相主要是地幔折射波，并不同于地方震的P波直达波。不同地震的震源深度存在较大差异，也可能导致视出射角计算差异。由此可见，视出射角的计算机化操作尚且存在一定的困难，不能作为近震与远震识别的判断依据。

2.2 主周期

主周期的计算是通过基于Morlet小波的时频分布来确定地震波信号主频的。小波变换能够提供能谱分析，准确提取信号的瞬时振幅和瞬时周期。地震波记录具有时变特性 (或称非稳态性质的信号)，我们需要知道在某一时刻可能出现何种震相，以及每一时刻在信号中所包含的频率成分。小波变换具有极好的定位特性，可在时间域、频率域或尺度域定位，在时间—频率域中分辨率随频率变化:低频时，使用大尺度值、长周期的小波函数;高频时，使用小尺度值、短周期的小波函数，这一变换特别适合于地震信号的表示和处理 (刘希强等，2000)。图3为即墨台初至P波到达后的一段地震信号，图4为从初至P波到达后截取5.12 s进行主频计算的结果图。

图3 即墨台初至P波到达后的地震信号Fig.3 Seismic waveform after initial P wave arriving in Jimo Station

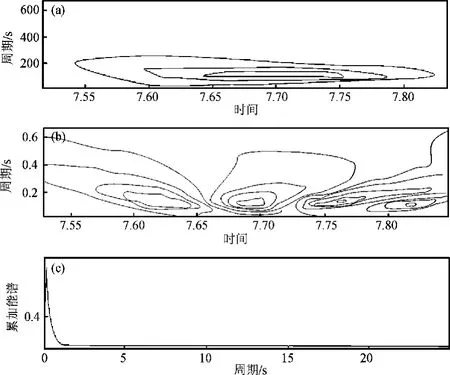
图4 主频计算结果图(a)能量分布图;(b)波振周谱分布图;(c)不同周期信号的能谱分布图Fig.4 Results of dominant frequency calculation(a)energy distribution;(b)distribution of wavelet amplitude spectrum;(c)energy distribution of signals in different periods

3 近震与远震识别

在区域自动定位系统中，以往的做法往往采用前几个波的平均周期 (用给定时间窗内的振动过零点个数估算)作为判断依据，而分界线周期是凭经验给定的，具有任意性。本文采用基于Morlet小波的时频分布来确定地震波信号主周期，采用神经网络学习得到合理的判断依据。选取山东地震台网记录到的共200个近震和远震的样本数据，窗长为P波到达后2～6 s，一般选择5.12 s为计算主周期的窗长。

3.1 样本收集

采用BP神经网络方法建模的首要条件是有充足的典型性好且精度高的样本。训练集的选择是BP神经网络能够成功的关键步骤之一，本文选取了100个近震样本和100个远震样本。近震与远震识别主要服务于山东区域地震自动定位系统，因此近震选取了黄海、青岛震群、冀鲁豫交界地区等山东区域内的地震作为样本;远震选取了台湾、四川、青海、西藏、新疆、福建等地的远震作为样本 (表2)。

3.2 神经网络训练

BP网络训练就是通过应用误差反传原理不断调整网络权值，使网络模型输出值与已知的训练样本输出值之间的误差平方和达到最小值或小于某一期望值。目前虽有已改进的BP算法、遗传算法 (GA)和模拟退火算法等多种优化方法运用于BP网络的训练，且这些方法可通过调整某些参数求得全局极小点，但在应用中，这些参数的调整往往因各种问题，较难求得全局极小点。其中应用最广的是增加了冲量 (动量)项而改进的BP算法。学习率影响系统学习过程的稳定性，过高的学习率可能使网络权值每一次的修正量过大，甚至会导致权值在修正过程中超出某个误差的极小值呈不规则跳跃而不收敛;而过低的学习率虽导致学习时间过长，但能保证收敛于某个极小值。所以，一般倾向选取较低的学习率以保证学习过程的收敛性 (稳定性)，通常选取0.01～0.8。增加冲量项的目的是为了避免网络训练陷于较浅的局部极小点。理论上其值大小应与权值修正量的大小有关，但实际应用中一般取常量。

为了保证算法的收敛性，学习率η必须小于某一上限，一般取0＜η＜1，而且越接近极小值，由于梯度变化值逐渐趋于零，算法的收敛就越来越慢。在网络参数中，学习率η和动量因子α的取值直接影响到网络的性能，主要是收敛速度。为提高学习速度，应采用大的η。但η太大却可能导致在稳定点附近振荡，乃至不收敛。针对具体的网络结构模型和学习样本，都存在一个最佳的学习率η和动量因子α，取值范围一般为0～1，视实际情况而定。笔者在上述范围内通过对不同的η和α的取值进行了试验，确定本文神经网络模型的参数为:η=0.7，α=0.9。在网络训练过程中应根据实际情况预先确定误差界值。误差界值的选择完全根据网络模型的收敛速度大小和具体样本的学习精度来确定。当Emin值取得较小时，学习效果好，但收敛速度慢，训练次数增加。当Emin值取得较大时，则相反。本文神经网络的误差界值Emin为0.000 01，即在迭代计算时误差值E＜Emin=0.000 01时，则认为学习完成，停止计算，输出结果。在训练中最大允许的相对误差是0.000 001，设置的节点数为2 000，这一精度达到了要求。

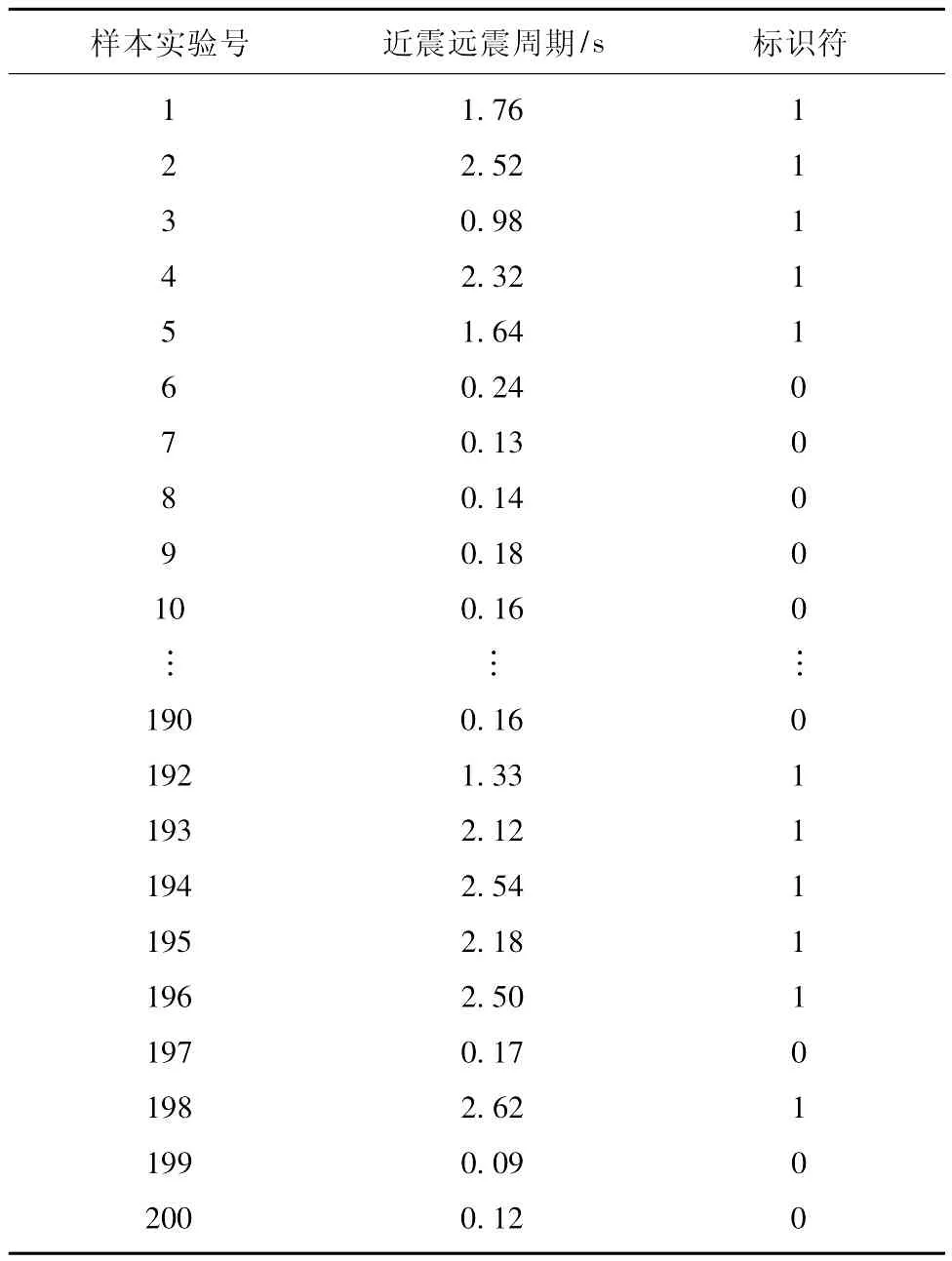
表2 近震远震训练样本Tab.2 Training samples of near and distant earthquakes

3.3 测试结果

为了验证BP神经网络的实用性，笔者利用BP神经网络程序对200个地震波形样本数据进行了训练，并将计算结果和理论标识结果进行了对比，给出检验数据个体的置信水平 (即置信度) (表3)。本文采用了全面的检验数据，对目前测震台网接收到的地震信号周期从0.06 s到4.5 s逐个进行了检验。在实际选取地震波样本数据的过程中，发现近震周期一般在0.06～0.25 s范围内。理论上我们规定近震标识符为0，通过1～9号实验数据计算的预测结果几乎都完全接近0，置信度达到100%，表明计算结果与理论标识结果完全相符。在实际选取远震样本数据时，远震周期范围较广，一般周期大于0.9 s，选取的样本数据主要集中在1～3 s，也有5 s以上的，本文设定最大范围参数为5 s，大于5 s的标识符认为是1。通过13～18号数据可以发现预测结果几乎都完全接近于1，置信度达到100%，表明预测结果非常理想。在检验数据中的0.25～0.9 s区间，是样本数据的空白区，应该是网缘地震震相主周期区间。仅就近震远震的识别而言，通过采集大量样本数据的非线性识别，0.35 s以下偏重于近震的成分较多，0.5 s以上偏重于远震的成分较大。

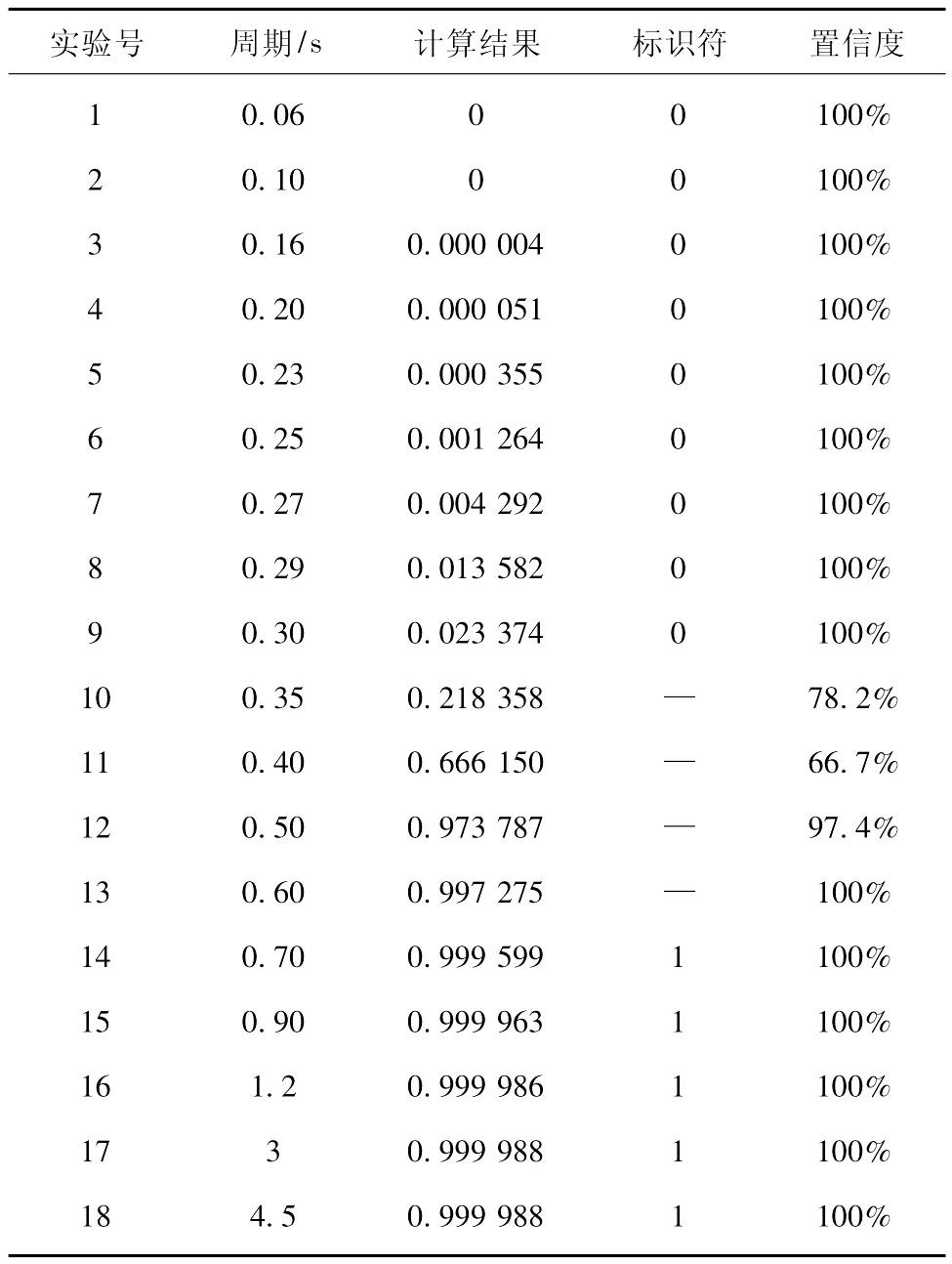
表3 近震远震检验结果Tab.3 Testing result of near and distant earthquakes

4 结论与讨论

近震和远震的自动识别是一个非常复杂的问题，把神经网络理论引入到该领域是一个新的尝试。BP神经网络具有优良的非线性逼近能力，本文成功地将BP神经网络用于复杂非线性系统模式识别的技术路线具有一定的创新性，对地震震相识别等问题具有很大的参考价值。

(1)通过对初至P波特征信息的讨论，笔者认为振幅、到时差、视出射角等都不能作为近震与远震识别的判断依据。对同一个地震，虽然视出射角随震中距增加呈现逐渐变小的趋势，但是在计算过程中发现近震与远震视出射角没有明显的差异。

(2)本文的检验数据在样本训练区间，预测结果置信度达到100%。在非样本区间 (样本区间向外延伸一定范围)也能够迅速收敛到标识符0或1附近，近震样本信号周期最大0.25 s，而置信度达到80%以上的预测区间几乎接近0.35 s;远震样本信号最小周期为0.9 s，而置信度达到80%以上的预测区间达到0.5 s，表明模型建立得当，具有良好的泛化能力。

(3)作为区域测震台网自动定位系统，只要判断为近震的置信度低于80%，即可定义为非处理地震事件。本文的研究虽然足够满足区域测震台网的需要，但是神经网络作为非线性识别系统，应增加更多体现波形特征的输入元，以后将进一步研究近震与远震震相差异的特征信息，使神经网络发挥更好的识别效果。

(4)由于地震波形的区域性和不同台网之间地震仪器的差别，目前在近震与远震识别方面的发展趋势仍然是从区域测震台网实际需要出发，充分利用台网的现有波形资料和地震的区域特点，建立尽可能多的样本数据，增加特征控制参数，将BP神经网络方法应用到更广泛的震相识别中。在自动定位系统中，爆破、地震、矿震波形的差异，地方震、网缘地震、远震等地震的识别都是对自动定位系统的一项挑战，掌握这些波形的特征信息，设置有效的参数，尽可能地全面训练各种样本，将大大提高自动定位震相判断的准确性。

致谢:赵仲和研究员对本文提出建议和思路指导，在此表示衷心感谢。

蔡煜东，宫家文，甘俊人，等.1994.地震序列类型预测的人工神经网络方法［J］.地震研究，17(1):40－45.

何斌，张元生，李稳.2010.计算地震初至波视出射角方法［J］.西北地震学报，32(1):11－15.

刘希强，周惠兰，沈萍，等.2000.用于三分向记录震相识别的小波变换方法［J］.地震学报，32(2):125－131.

穆星.2005.利用地震几何属性和自组织神经网络进行地震相得自动识别［J］.地质科技情报，24(3):109－112.

王娟，刘俊民，范万春.2004.神经网络在震相识别中的应用［J］.网络与通信，(5):35－37.

赵仲和.2005.地震自动定位的综合解决方案［J］.地震地磁观测与研究，26(2):50－56.

中国地震局监测预报司.2007.地震学与地震观测［M］.北京:地震出版社.

Allen.1978.Automatic earthquake recognition and timing from single traces［J］.BSSA，68(5):1521 －1532.

Cichowicz.1993.An automatic S － phase picker［J］.BSSA，83(1):180－189.

Coforth T，Herin E.1981.An automatic seismic signal detection algorithm based on the walsh transform［J］.BSSA，71(4):1 351 －1 360.

Jin W，Ta-Liang T.1988.Artificial neutral network based seismic detector［J］.BSSA，85(1):308 －319.

Identification between Near and Distant Earthquakes Based on Neutral Network

QU Jun-hao，LIU Xi-qiang，WU Dan-tong，ZHANG Qin，YU Cheng，MU Juan，MIAO Qing-jie
(Earthquake Administration of Shandong Province，Jinan 250014，Shandong，China)

We studied seismic waves near the P wave phase to discuss the characteristic of near and distant earthquakes.Firstly，we selected main period of initial P wave as the input element of neural network and picked up 2 ～6 s of initial P wave arriving time as time window of seismic wave.Secondly，we chose the right network structure and parameters and collected a large number of earthquake training data to realize the nonlinear system identification between near and distant earthquake.The results show that the predictable result of test data whose confidence reaches 100%in sample training interval can converge to identifier 0 or 1 quickly in non-sample training interval.The maximum period of near earthquake sample is 0.25 s and its prediction interval whose confidence reaches more than 80%is almost close to 0.35 s.The minimum period of distant earthquake sample is 0.9 s and its prediction interval whose confidence reaches more than 80%is 0.5 s，which shows that the model we select is proper and has good generalization ability.

BP neutral network;near earthquake;distant earthquake;phase identification

P315.6

A

1000－0666(2012)03－0360－07

2011－11－30.

山东省自然科学基金 (Y2007E09)，山东省科学技术发展计划项目 (2009GG10008002)和山东省地震局重大基金项目 (JJ1105Y)联合资助.