云南地震灾害人员伤亡预测方法研究*

施伟华，陈坤华，谢英情，李 西，庞卫东，代博洋

(云南省地震局，云南昆明650224)

云南地震灾害人员伤亡预测方法研究*

施伟华，陈坤华，谢英情，李 西，庞卫东，代博洋

(云南省地震局，云南昆明650224)

以1992～2010年云南地区的破坏性地震的伤亡人数资料为主，将其分别与地震震级和烈度统计拟合，得到云南地区震级和烈度与死亡人数的关系曲线及表达式。根据云南各地的自然环境和社会发展的差异，确定了各种条件下的地震灾害人员死亡影响因子加权系数的取值，对两个拟合关系表达式进行校正。采用该方法计算了已发生的12个地震的死亡人数，并与实际的地震灾害死亡人数作了对比及讨论。

破坏性地震;地震灾害;人员伤亡;云南地区

0 前言

破坏性地震发生后，对伤亡人员进行救治与处理是地震救灾最为紧要及主要的任务。救灾力量投入的大小与人员伤亡数量密切相关。了解灾区的现状、决策救灾的规模、派遣合适的救灾人员与设备，是决策人员面对的首要问题，因此有必要寻求一种较好的预测方法，在地震发生后的数小时内，对该次地震的人员伤亡情况进行预先评估，及时布署抗震救灾工作。

国内地震人员伤亡预测方法主要有:房屋毁坏率法 (谭承业，1989;尹之潜，1991;晏凤桐，2003)、动态评估法 (周素琴，2004)、灾情拟合法 (施伟华等，2005)等。这些方法以地震灾害调查统计资料为基础，多数以房屋破坏状况为造成人员伤亡的主要因素，以发震时间、人口密度等作为影响因子，从而得到人员伤亡快速预测公式。

本文结合云南的历次地震人员伤亡统计资料、将地震动强度作为造成人员伤亡的主要因素，以社会发展和自然环境等作为影响因子，对云南破坏性地震后的伤亡人数快速预测方法进行研究，以寻求一种简便、快捷而又具有一定实用性的预测地震灾害人员伤亡的方法。

1 资料选取与方法概述

1.1 资料选取

云南地区自1992年进行地震灾害损失评估以来，积累了丰富的地震灾害人员伤亡资料。本文以1992～2010年云南地区历次地震的震级和烈度与死亡人数的资料为主，由于在这期间云南的大地震数量少，为了减小统计拟合的离散和误差，增加了1970年通海7.8级、1974年永善—大关7.1级、1976年龙陵7.4级和1988年澜沧—耿马7.6级4个大地震，及对自然环境和社会发展影响相似的2008年四川汶川8.0级、2010年青海玉树7.1级2个大地震。

地震人员伤亡资料主要来源于云南地区历次地震灾害损失评估报告，本文只选取灾区 (烈度Ⅵ度及其以上)全部在云南境内的地震，这样比较合理。1992～2010年，云南境内共发生49次破坏性地震，加上上述的6个地震，本文共使用55个地震 (表1)。文中涉及的云南省和各县的人口密度来源于云南统计年鉴或相关资料。

1.2 方法概述

由表1统计拟合得到云南震级和烈度分别与死亡人数的拟合曲线及关系式，用这两个拟合关系式可以计算出在不同震级和烈度下的地震伤亡人数。

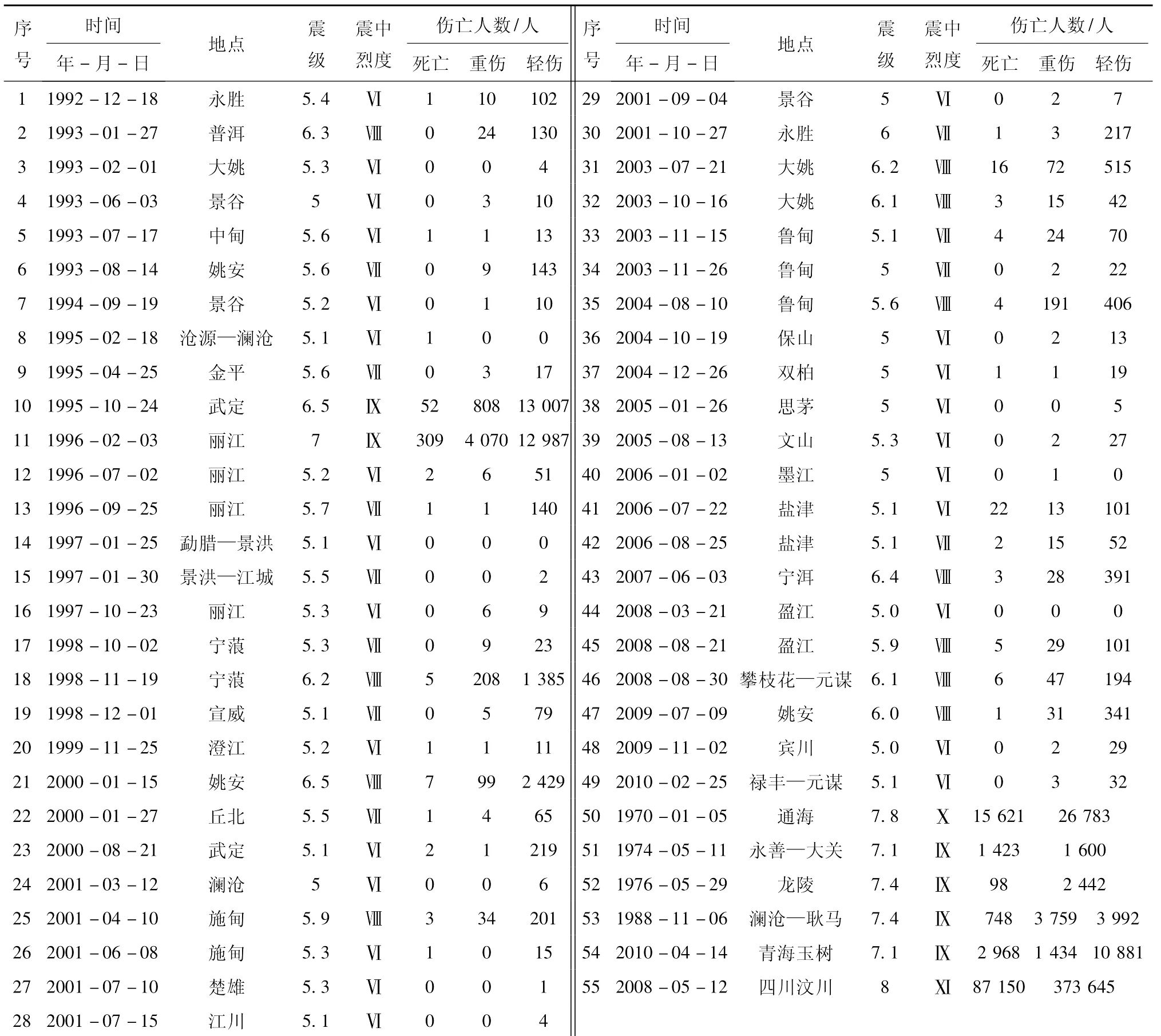
表1 历次地震伤亡人数统计表Tab.1 Statistics of the number of earthquake casualty

地震伤亡人数主要取决于地震能量 (震级或烈度)的大小，并与灾区的人口密度以及发震时间相关，还受震区的地形与天气、震中位置和有无显著前震的影响。云南各地的自然环境和社会发展的差异大，对于某一地区来说，应该用人口密度加权系数 (某震区的人口密度与云南省的人口密度之比)、发震时间加权系数、地形天气加权系数、震中位置加权系数和显著前震加权系数来对拟合计算得到的地震灾害死亡人数D'进行校正。

地震灾害死亡人数的预测函数为

式中，D为预测计算死亡人数;D'为拟合计算死亡人数;R为影响因子加权系数组，由一系列加权系数组成:人口密度加权系数ρ;发震时间加权系数T;地形天气加权系数G;震中位置加权系数P;显著前震加权系数W。

则地震灾害死亡人数的预测函数展开式为

2 地震灾害死亡人数的统计拟合

2.1 震级与死亡人数的拟合

用表1中的不同震级与死亡人数，统计拟合得到云南震级与死亡人数的关系曲线 (图1)，其关系式为

式中，D'为拟合计算死亡人数;M为震级。

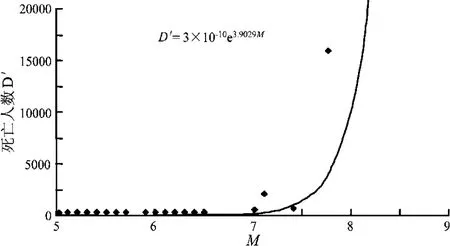
图1 云南地区震级与死亡人数的关系Fig.1 The relationship between magnitude and the number of deaths in Yunnan

2.2 烈度与死亡人数的拟合

用表1中的不同烈度与死亡人数，统计拟合得到云南烈度与死亡人数的关系曲线 (图2)，其关系式为

式中，D'为拟合计算死亡人数;I为烈度。

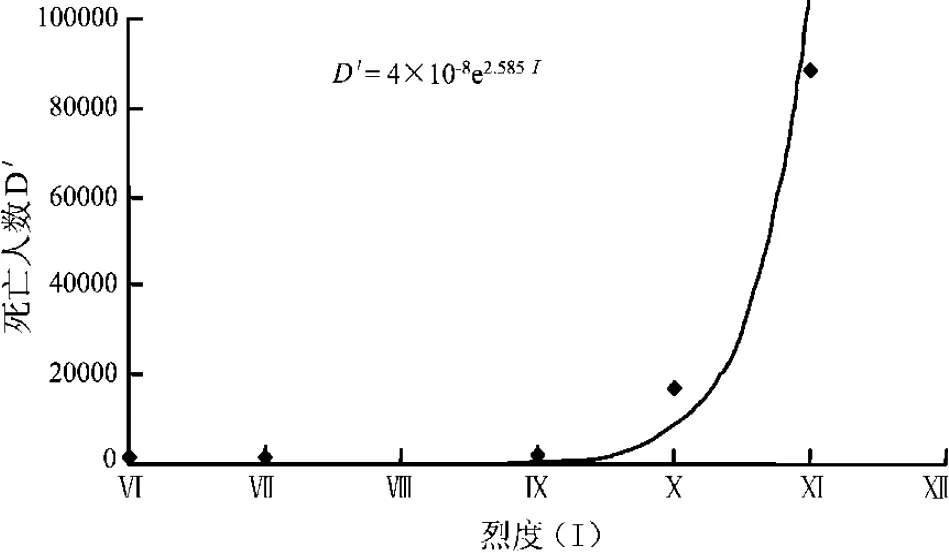
图2 云南地区烈度与死亡人数的关系Fig.2 The relationship between intensity and the number of deaths in Yunnan

3 影响因子加权系数的确定

3.1 ρ的确定

震区的人口密度对人员伤亡有很大的关系。人口密度每年都有变化，所以ρ(某震区的人口密度与云南省的人口密度之比)的取值应在地震发生后查阅发震时的云南省与发震地的上年统计年鉴计算得到，或者由数年前的云南省与发震地的人口密度乘以年增长率得到。

3.2 T的确定

发震时间对人员伤亡有较大的影响。王景来和杨子汉 (1998)通过大量的调查，根据云南地区 (特别是农村)居民的生活、生产习惯，给出了云南地区各时段的人员户外率，笔者根据各时段的人员户外率，给各时段赋予一个人员发震时间加权系数 (表2)，T的取值见表2。

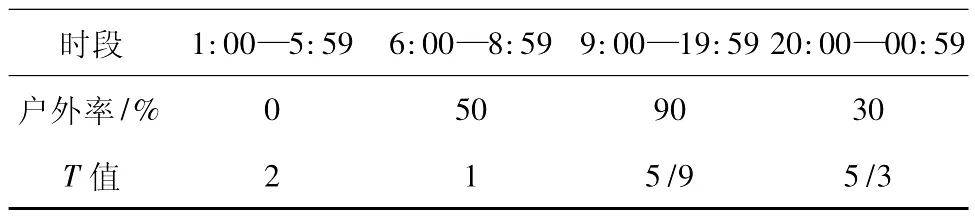
表2 云南各时段人员户外率及发震时间加权系数TTab.2 Ratio of staff in outdoor in every time period and weighting coefficients occurrence time T of earthquake in Yunnan

3.3 G的确定

震区的地形与天气对人员的伤亡有影响。由表1可知，云南发生同样烈度的地震，其伤亡人数有几倍乃至几十倍的差别，原因诸多，其中有地形与天气的影响。差别最大的是Ⅵ度地震，最少死亡0人，最多死亡22人。2006年盐津5.1级地震死亡人数22人，其中18人为滚石和崩塌体致死，创造了云南地震史上的死亡之最。其主要原因是震区地形陡峭、山体破碎，又正值雨季，加重了塌方和滚石。2008年四川汶川8.0级地震由于地形引起滑坡、塌方和滚石，造成过多的伤亡。2010年青海玉树7.1级地震的灾害偏重，除了房屋抗震力弱外，也有这方面的原因。此外软弱松散、抗震力弱的场地也会加重人员伤亡。本文G的取值见表3。

表3 云南地形天气加权系数GTab.3 Terrain and weather weighting coefficient G in Yunnan

3.4 P的确定

城镇与农村的人员活动范围不同，前者主要是室内活动，后者主要是室外活动。另外，城镇是整个地震灾区的人口密集之地，其人口密度高于整个地震灾区的人口密度。基于这两个原因，震中离城镇的距离对伤亡人数的影响较大，是地震人员伤亡预测的因素之一。以云南盈江2008年8月21日5.9级和2011年3月10日5.8级两次地震作对比。盈江5.9级地震发生于盈江县北部山地的勐弄乡左家坡—中山村—勐弄村一带，离盈江县城41 km。盈江5.8级地震发生于盈江盆地的县城至盈江农场一带，离盈江县城2 km。两次地震的伤亡人数见表4。盈江县的基本抗震设防烈度为Ⅶ度。

表4 盈江5.9级和5.8级地震的伤亡人数Tab.4 Earthquake casualties of Yingjiang M5.8 and M5.9 earthquakes

由表4可以看出，伤亡数量差别很大，盈江5.8级地震的死亡人数是5.9级地震的5倍之多。这主要由于震中离县城近，而且地震造成的烈度达Ⅷ度，超过了盈江基本设防烈度，其次还有盈江盆地的场地土软弱松散的影响。以盈江两次地震的伤亡对比为依据，将伤亡人数与震中距的关系作一些前推和后延，笔者认为当地震造成的烈度超过当地的设防烈度Ⅰ度时，P值可以按表5取值，超过Ⅱ度时可以考虑将P值加倍。当地震造成的烈度小于或等于当地的设防烈度时，在预测计算时可以忽略震中位置加权系数。

表5 云南震中位置加权系数PTab.5 Epicenter location weighting coefficient P in Yunnan

3.5 W的确定

本文所指的显著前震是主震前数天内发生、有强烈震感、没有造成重大人员伤亡、对减少后续大震的人员伤亡有预警作用的地震。相近自然环境与社会环境下的相似地震的人员伤亡对比研究，对认识生命损失影响因数具有一定意义。李永强和王景来 (2007)揭示了1976年5月29日云南龙陵7.3级、7.6级与1988年11月6日澜沧—耿马7.4级、7.2级地震的显著前震对人员伤亡的影响 (表6)。

表6 1976年龙陵、1988年谰沧—耿马地震的主要参数Tab.6 Main parameters of Longling earthquake in 1976 and earthquake in 1988 Langcan-Gengma

从表6看出，同是云南西部澜沧江以西的双震型大震，震级、发震时间、人口密度相近，自然环境与社会环境相似，极震区烈度均为Ⅸ度，但人员死亡数量相差很大。据此，在有显著前震的情况下，本文将W的取值定为0.2，如没有显著前震，W的取值为1.2(表7)。

表7 云南显著前震加权系数WTab.7 Weighting coefficient W of notable foreshock in Yunnan

4 重伤、轻伤人数的估算

表8为笔者统计的1992～2010年云南地区各烈度地震伤亡人数及比率。

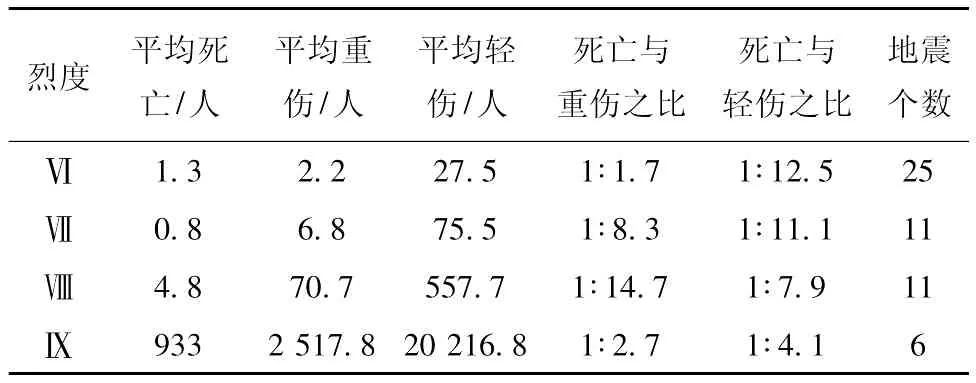
表8 地震烈度与人员死伤比的关系Tab.8 Relationship between intensity and ratio of deaths and casualty

王景来和杨子汉 (1998)通过对云南1950～1996年的54次震中烈度达到Ⅵ度以上的地震的人员死伤比进行研究，发现死伤比与烈度有很大的关系，烈度低的地震死伤比要小得多，随着烈度的增加，死伤比越来越大，它们的关系见表9。以表8的统计计算结果为主，参考表9的结论，笔者给出云南死亡与重伤的比例、死亡与轻伤的比例 (表10)。

表9 地震烈度与人员死伤比的关系Tab.9 Relationship intensity and rutio of deaths and casualty

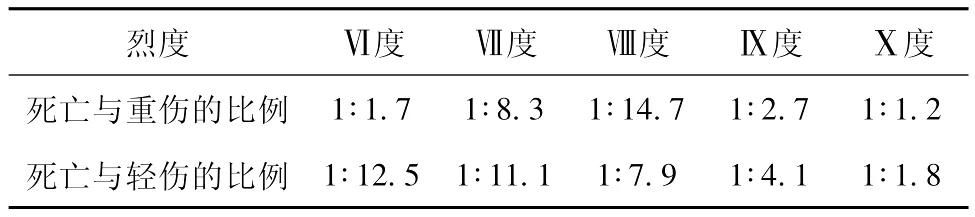
表10 云南死亡与重伤、死亡与轻伤的比例Tab.10 Ratios of deaths and serious injuries，deaths and minor injuries in Yunnan

5 预测实例与讨论

5.1 预测实例

发生地震后，知道震级且取得该地震灾区的人员伤亡影响因子加权系数，用震级与死亡人数的拟合关系式 (3)和死亡人数的预测函数展开式 (2)，可以预测计算出该地震的死亡人数 (简称震级法)。

已知地震的震级和震源深度，用震中烈度与震级的关系式I0=1.5M－1.2 lgh+0.75(胡聿贤，1988)求出该地震的震中烈度。取得震中烈度和该地震灾区的人员伤亡影响因子加权系数，利用烈度与死亡人数的拟合关系式 (4)和死亡人数的预测函数展开式 (2)，可以预测出该地震的死亡人数 (简称烈度法)。

笔者选取了云南地区12个具有代表性的不同震级的地震，其中包含了2006年7月22日的盐津5.1级地震，根据各地震发生地的实际情况，取得各个影响因子加权系数值，用上述两种预测方法，计算预测了人员死亡数，并与实际死亡人数作对比，见表11。

表11 两种预测方法的结果与实际死亡人数的对比Tab.11 Number of deaths comparison between two prediction methods and in actural

5.2 讨论

从表11可以看出，在烈度法中12个预测样本有8个的预测结果非常接近实际的死亡人数，而且在8个预测结果中，Ⅷ、Ⅸ度的地震有4个。在震级法中12个预测样本有4个地震的预测结果非常接近实际的死亡人数，但这4个都是Ⅵ、Ⅶ度的地震。两种预测方法的相对可信度的差异，与两种方法的拟合对象不同有关，震级法的拟合数据稳定性差、离散大，而烈度法则好一些。造成这种差别的原因主要是各地的情况差异很大，地震灾害死亡人数受诸多因素的影响，造成同等震级或烈度的地震，其死亡人数有几倍乃致十几倍的差异 (表1)，数据波动大，且地震是小概率事件，统计拟合的样本数偏少，特别是大地震和特大地震，所以造成了拟合的离散，产生了误差。

两种预测方法对盐津5.1级地震死亡人数的预测结果与实际死亡人数的差别都很大，这说明盐津地震的情况是个特例，在云南是罕见的。说明地震灾害人员伤亡预测的难度大，影响因子加权系数的取值很重要，特别是在云南，各地的自然环境千差万别，社会发展水平参差不齐，会有特殊情况发生，在预测伤亡人数时，需要熟悉云南的情况。

综上所述，笔者认为两种预测方法与实际死亡人数都存在误差，但烈度法的预测结果比震级法更接近实际，特别是发生高烈度的地震时。影响因子加权系数的取值范围的确定是难点，需要进行大量的调查考证工作，以对其考察、改进和完善。

发生地震后，用烈度法进行人员伤亡预测具有一定的参考价值。已知死亡人数，用表10的死亡与受伤的比例就可以预测受伤人数，由于篇幅的关系，本文省略。

胡聿贤.1988.地震工程学［M］.北京:地震出版社.

李永强，王景来.2007.云南地震灾害与地震应急［M］.昆明:云南科技出版社.

施伟华，周光全，卢永坤.2005.云南地震人员灾情预估方法初探［J］.地震研究，28(3):294 －297.

谭承业.1989.发布地震告警的一个判据——各类地震死亡人数预测［J］.中国地震，5(4):81－88.

王景来，杨子汉.1998.云南自然灾害与减灾研究［M］.昆明:云南大学出版社.

晏凤桐.2003.地震灾害的快速评估［J］.地震研究，24(4):382－387.

尹之潜.1991.地震灾害预测与地震灾害等级［J］.中国地震，7(1):9－19.

周素琴.2004.地震人员伤亡的动态评估［J］.华侨大学学报，32(1):16－21.

Prediction Method Research on Casualties Due to Earthquake Disaster in Yunnan

SHI Wei-hua，CHEN Kun-hua，XIE Ying-qing，LI Xi，PANG Wei-dong，DAI Bo-yang
(Earthquake Administration of Yunnan Province，Kunming 650224，Yunnan，China)

Using the data of the number of casualties due to destructive earthquake in Yunnan area from 1992 to 2010，we fitted curve and expressions between magnitude，intensity and deaths respectively.According to the difference of natural environment and social development among various places in Yunnan，we identified weighting coefficients values of casualty's impact factor in earthquake disaster under various conditions and used weighting coefficients to calibrate the two expressions of fitting relation.At last，we applied this method to estimate the death number of 12 earthquakes and compare with the actual number of death in actual earthquake disaster.

destructive earthquake;earthquake disaster;casualty;Yunnan area

P315.94

A

1000－0666(2012)03－0387－06

2012－04－05.

地震行业科研专项“宁洱6.4级地震现场综合考察和研究 (200808061)”资助.