析取克里格法在可回采资源量的总体估算的应用

郭奇峰，刘金辉

(北京科技大学土木与环境工程学院，北京 100083)

地质统计学方法是目前空间分析中最有效的方法之一，广泛应用于油藏描述[1-2]，煤田储量分析[3]、金属矿山储量计算以及工程地质[4-6]参数估计中。在金属矿采矿过程中，现代的非线性统计学方法主要用于小的采矿单元的金属量和储量总体估算。典型的非线性地质统计学方法有：指示克里格法(Indicator kriging)、概率条件期望法(Probability from Conditional Expectation)、析取克里格法(Disjunctive kriging)、统一条件法(Uniform conditioning)和服务变量法(Service variables)等[7]。

由于经典的线性克里格估算方法无法用于估算一个与矿体成非线性关系的变量，而条件期望值法又需要很多难以获得的原始数据[8]，所以，法国数学家Matheron[9]于1975年提出了析取克里格法，将克里格方法系统化理论化，使克里格技术得到很大的提高[10]。本文主要针对析取克里格法基本算法和空间结构，应用析取克里格进行可回采资源量总体估计方面的研究，解决线性空间统计学在这方面的不足。

1 析取克里格方法简介

线性地质统计学方法只能估计真值Z(x)的值Z*(x),不能估计Z(x)的函数，而可采储量和矿石的平均品位都是Z(x)的函数，线性统计学方法不能够估计Z(x)的空间变异性。假设已知任意的两个区域变化量(Zα,Zβ)及(Zο,Zβ)全部的二维概率分布，应用非线性地质统计学如析取克里格方法，可以解决线性方法空间统计信息不足的问题[11]。析取克里格方法介于条件期望与线性估计之间，前提假设Z(x)服从一、二元正态分布，并利用厄尔米特多项式展开进行估计，其一般形式为：

(1)

式中，fa(Za)是每一个有效数据变量Za的函数，a=1,2,…,n。

2 高斯变换模型与厄尔米特多项式

在可采储源量估算中，析取克里格法是利用离散高斯模型来估计局部可采资源储量的一种方法。高斯渐变是一个数学函数变换，在一个任意分布新的变量Z中，将变量Y进行高斯变换分布，即Ζ=φ(Y),该方程式可表示为以下多项式：

(2)

上式中为埃尔米特多项式，其定义为：

(3)

厄尔米特多项式属于特殊函数中的一种正交多项式。

3 析取克里格在可回采资源量中的估算模型

在离散高斯模型下，应用析取克里格方法估算局部可采储量，其目的是计算平均品位高于边界品位的盘区内块体的可采矿石吨位和金属量。 实践中，我们将样品置于块体中心，并利用置中心样品计算厄尔米特多项式。这些多项式将被用于克里格方程阶，对于每个盘区，克里格化的多项式表示为：

(4)

应用克里格化的多项式，可以得出可回储量T：

(5)

金属量Q：

(6)

平均品位m：

(7)

4 应用实例

某一金矿床类型属于后生韧性剪切带脉金硫化物类型。韧性剪切带型金矿也称韧-脆性剪切带型金矿或含金剪切带型金矿，是指受韧性和韧-脆性剪切构造体系控制的矿床，既包括传统的含金石英脉，也包括由各类岩石破碎蚀变形成的浸染型矿床。金矿化是在长期的剪切作用过程中逐渐形成的，剪切作用不仅是控矿因素，而且是一个重要的成矿机制[4]。该类型矿体具有规模较大、厚度变化不大、品位变化系数较大等特点。因此，对此类矿床，应用传统的资源量估算方法容易产生较大误差，但很适宜应用地质统计学方法进行估计与模拟。

研究区域主要由两条相互平行彼此相距9km的Kalbinsk和Northwest断裂带构成，二者走向均为NW40°，倾向NE，倾角60°～70°。左旋运动所产生的压力，沿着这两条主要断裂带形成了分布于二者之间的近EW向脆韧性变形带Kyzyl剪切带(KSZ)和与之平行的Parallel剪切带(PZ)。区内主要的金矿床均产出于KSZ和PZ这两条剪切带内，以及与Kalbinsk和Northwest断裂带的交叉部位。KSZ剪切带横切石炭纪沉积岩，长11.5km，宽10～240m，走向近EW，倾向N，倾角30°～40°。该剪切带内部具复杂的渐进式脆性-塑性变形特征，表面叠加了连续的硅化、硫化物蚀变。前苏联钻探资料表明，其向下延伸1.5～3.5km，接近下伏花岗岩。PZ剪切带位于KSZ剪切带北部5km左右，走向近EW，倾向N，倾角40°，宽10m至几十米。近矿围岩蚀变强烈，以“硅化+绢云母化+绿泥石化+铁碳酸盐化+黑云母化”为特征。金矿化与强烈的硅化石英脉、石英网脉相伴发生，同时与强烈的针状毒砂、细粒黄铁矿化密切相关，可以概括为针状毒砂+细粒黄铁矿+硅化+石英网脉是Bakyrchik金矿最重要的矿化蚀变组合。前人研究资料表明，载金矿物主要为毒砂，毒砂粒度极细，主要分布在1～3μm和90～1500μm间。金主要分布于毒砂矿物的晶格及表面裂隙中，金粒度一般为10μm。本次研究主要对于No.9～10号矿体，通过地表和地下坑道，圈定了该矿化带。

在地表与坑道钻探的基础上，应用析取克立格方法对资源进行重新评价和布置未来的开采计划。其高斯变换模型与厄尔米特多项式的分布函数，如图1所示。

块上的高斯变化支持10m×10m×10m。经过量化后的支撑效应，支撑效应分析结果如下表1。

表1 块体支撑效应修正计算结果

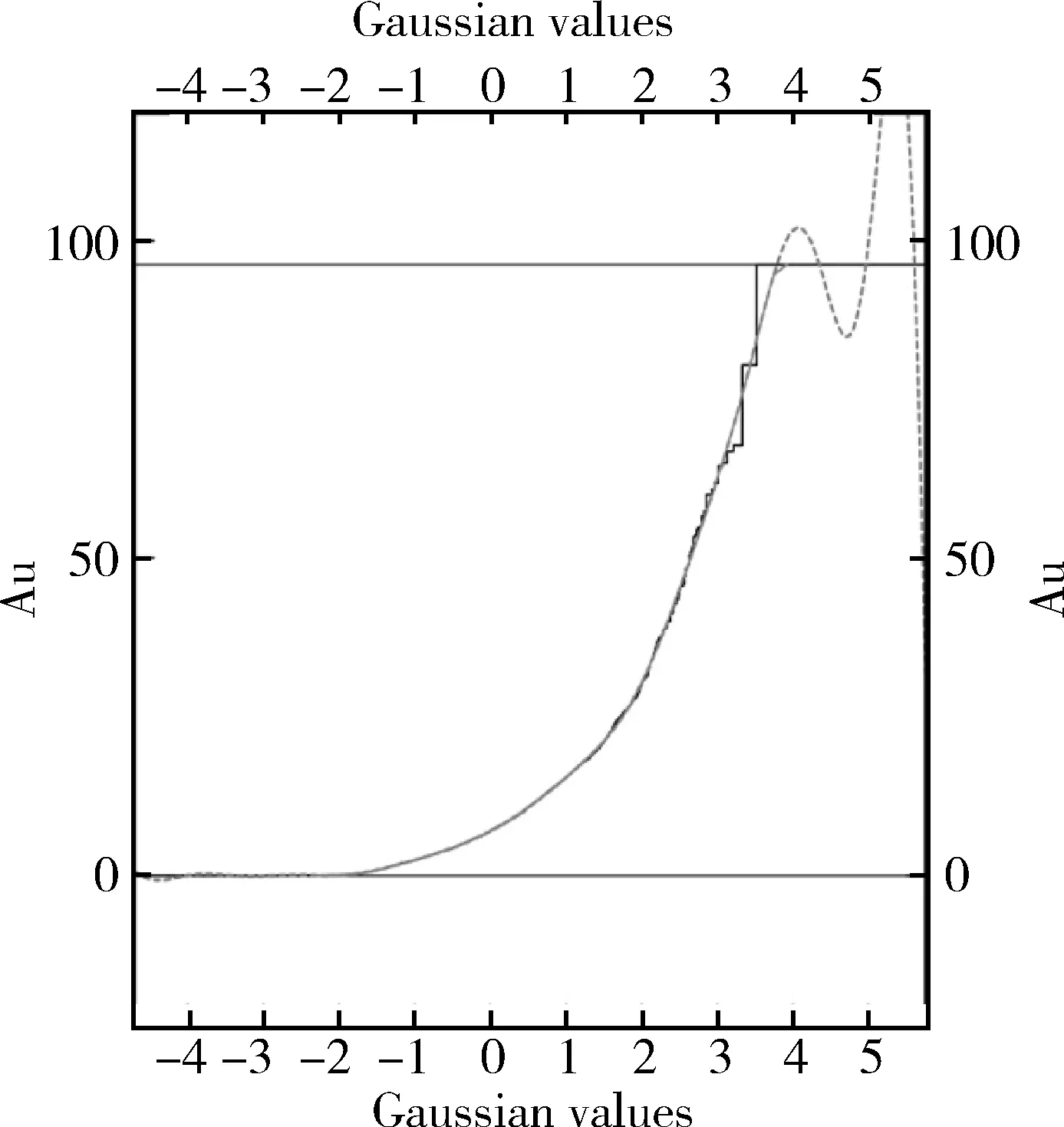
图1 点状的高斯变换方程

支撑效应作用后，其块体直方图模型较点状直方图模型更为平滑，如图2所示。

图2 块体与点状直方图(块体为黑色，点状为深灰色)

5 结论与评价

由上面图形分析可知，在可回采资源估算时，析取克里格方法解决了线性地质统计学中品位高平滑方面的问题，避免了线性估算方法带来的平滑效应。品位频率分布是以特定的小的矿块为基础的，矿块的大小不同，频率也将不同。应用析取克里格法估算可回采资源，考虑到了采矿和边界品位方面，并且能在进行采矿之前来预测盘区可采储量，为将来的采区采场的布置、出矿配矿提供了必要的理论和实践依据。

[1] 纪发华，熊琦华，张一伟.地质统计学在油藏描述中的应用[M].北京：石油工业出版社，1997.

[2] 李庆谋.多井处理与油藏描述[J].吉林油田科技，1989，18(1)：15-23.

[3] 张瑞新，韩金岩，刘光.胜利煤田1号煤层资源评价[EB/OL].http:∥www.gzit.edu.cn/gut/magazine/xb982/xb982-1/98xb21-7.html，2003-5-10.

[4] Guratscio M，David M，Huijbregts C J，eds.Advanced Geostatistics for the Mining Industry[M].Dortrecht，Netherlands：Reidel，1976.

[5] Verly G，David M，Journel A，et al.eds.Geostatistics for Natural Resources Characterization[M].Dordrecht，Netherlands：Reidel，1984.

[6] Armstrong Margaret ed.“Geostatistics”，Proceedings of the 3rdInternational Geostatistics Congress， Avignon，France，September 5-9,1988，Serie Quantitative Geology and Geostatistics，volume 4[M].Dordrecht， Holland：Kluwer Academic Publishers，1989.

[7] 侯景儒，尹镇南.实用地质统计学[M].北京：地质出版社，1998：68-72.

[8] 孙洪泉.地质统计学及其应用[M].北京：地质出版社，1981：211-218.

[9] Matheron G.Principles of Geostatistics[J].Principles of Geostatistics.Economic Geology，1963，58：1246-1266.

[10] 李庆谋.多维分形克里格方法[J].地球科学进展，2005(2)：248-256.

[11] Bleinès.C.,Bourges M.etc.France：ISATIS 8.0 Case Study[R],2008， 69-91.