基坑开挖数值分析中土体硬化模型参数的试验研究
王卫东 ,王浩然 ,徐中华
(1. 同济大学 地下建筑与工程系,上海 200092;2. 华东建筑设计研究院有限公司 地基基础与地下工程设计研究所,上海 200002;
3. 同济大学 岩土及地下工程教育部重点实验室,上海 200092)
1 引 言
随着经济的发展,上海软土地区的基坑规模越来越大,市区的基坑工程大多紧邻敏感的建(构)筑物如地铁隧道、地铁车站、老建筑及市政管线等。在这种情况下,基坑的支护结构除满足自身强度要求外还须满足变形要求,以保护周边环境。由于问题的复杂性,传统的解析方法或相关的规范方法[1-3]都难以合理地分析基坑开挖对周边环境的影响。数值分析方法[4-5]由于其能考虑土层的分层情况和土的性质、支撑系统分布及其性质、土层开挖和支护结构支设的施工过程以及周边建(构筑)物存在的影响等复杂因素,已成为深基坑工程分析的最有效方法。
数值分析方法中的关键问题之一是要采用合适的本构模型和计算参数。土体硬化本构模型能考虑软黏土的硬化特征、能区分加荷和卸荷的区别,且其刚度依赖于应力历史和应力路径,计算结果能同时给出较为合理的墙体变形及墙后土体变形,适合于敏感环境下的基坑开挖数值分析[6],因此,土体硬化模型已成为基坑工程数值分析中用的最多的模型之一[7-9]。新版的上海基坑工程技术规范[1]也推荐采用土体硬化模型进行基坑数值分析,但没有明确地给出上海各土层的计算参数。HS 模型参数较多,获取较完整的模型参数存在一定困难。目前,HS 模型参数的确定方法主要有根据工程实测数据的反分析法[10]和室内土工试验法[11]。单纯的反分析法仅能获取其中敏感性较强的参数,其他参数的确定还需要依赖工程经验,并且由于基坑工程的复杂性,所获得的实测数据有时也很难真实地反映工程的实际状态。室内试验法能直接测试土体的物理力学性能指标,是获取参数的有效方法。目前国内仅有刘畅[11]通过试验获得过天津地区土层土体硬化模型的部分参数,但还没有获得过较完整的土体硬化模型试验参数的报道。本文通过近半年的室内土工试验,较完整地测试了上海软土地区典型土层土体的HS 模型参数,并对参数中的模量关系做了分析。试验结果可为分析上海地区及其他类似软土地区的基坑工程数值分析参数的确定提供参考。
2 土体硬化模型及其参数简介
HS 模型为Plaxis 软件中的一种本构模型,由Schanz 等[12]提出。该模型为等向硬化弹塑性模型,其在主应力空间中的整个屈服面如图1 所示。土体硬化模型可以同时考虑剪切硬化和压缩硬化,并采用Mohr-Coulomb 破坏准则。
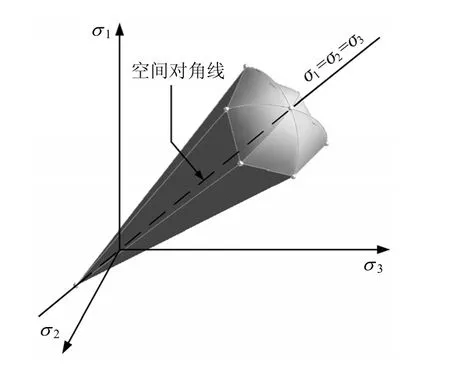
图1 主应力空间中的土体硬化模型屈服面 Fig.1 Yield surface of the hardening soil model in principal stress space
土体硬化模型能适合于多种土类的破坏和变形行为的描述[13],并且适合于岩土工程中的多种应用,如堤坝填筑、地基承载力、边坡稳定分析及基坑开挖等。土体硬化模型共有11 个参数,包括:有效黏聚力c′、有效内摩擦角φ′、剪胀角ψ 、三轴固结排水剪切试验的参考割线模量、固结试验的参考切线模量、与模量应力水平相关的幂指数m、三轴固结排水卸载-再加载试验的参考卸载再加载模量、卸载再加载泊松比νur、参考应力 pref、破坏比Rf、正常固结条件下的侧压力系数K0。
模型参数中的静止侧压力系数K0的确定可以参考文献[14],也可由K0=1-sinφ′[15]计算得出。根据Janbu[16]的研究,对于砂土和粉土,与模量应力水平相关的幂指数m 一般可取为0.5;对于黏性土,m 的取值范围为0.5~1[17]。卸载再加载泊松比νur可采用Plaxis 软件模型手册[17]中的建议值,一般取为0.2;参考应力 pref一般取为100 kPa;根据Bolton[18]的研究,对于砂土,剪胀角ψ 可取为(φ′-30°);对于黏性土,ψ 一般取为0[17]。因此,本文主要通过室内常规三轴试验和固结试验来确定模型的c′、φ′、、、和Rf。
3 试验内容及试验设备
3.1 试验内容
上海地区的基坑工程涉及到的土层主要是浅层软弱的土层,因此,本试验的土层主要是典型的黏土层②2、淤泥质粉质黏土层③、淤泥质黏土层④、粉质黏土层⑤3。试验内容包括3 部分,土体三轴固结排水剪切试验、三轴固结排水加载-卸载-再加载试验以及标准固结试验。三轴固结排水剪切试验测试土体的c′、φ′、和;三轴固结排水加载-卸载-再加载试验测试土体的 E;标准固结试验测试土体的。
3.2 试验设备
三轴固结排水剪切试验和三轴固结排水加载-卸载-再加载试验采用的设备是英国GDS 多功能三轴仪,如图2 所示。标准固结试验采用的设备是常规固结仪。

图2 GDS 设备图 Fig.2 Pictures of equipment of GDS
4 试验过程
4.1 现场取样
试验采集上海地区某一建筑工地4 个典型土层(②2、③、④、⑤3)的试样,其中③、④为软弱土层,因此,采取钻探结合薄壁取土器压入法取样。薄壁取土器外径为75 mm,壁厚为1.5 mm,长度为500 mm。薄壁取土器外形如图3 所示。4 个典型土层的基本物理参数指标见表1。

表1 典型土层基本物理参数指标 Table 1 Physical parameters of typical soil layers

图3 薄壁取土器图 Fig.3 Pictures of thin wall samplers
4.2 试验步骤
4.2.1 三轴固结排水剪切试验步骤
三轴固结排水剪切试验可分为4 个主要步骤:(1)反压饱和。试验前用真空抽气法对试样进行了预饱和。试验中又采用反压饱和法对试样进一步饱和。在试样顶部施加100 kPa 的反压力,同时在试样周围施加110 kPa 的围压,使土体内的气泡缩小,持续时间约为3 h。(2)B 值检测。保持反压不变,关闭反压阀门,围压增大30 kPa,在不排水的条件下测定孔隙水压力系数B。若B >95%,认为试样饱和。(3)固结。试样在围压3σ 下进行等向固结,固结稳定时间取为36 h。(4)剪切。排水剪切采用等应变速率控制,剪切速率为0.003 7 mm/min,以保证试样中的孔隙水有充足的时间排出。当试样的应变值达到20%时,停止试验。
4.2.2 三轴固结排水加载-卸载-再加载试验步骤
三轴固结排水加载-卸载-再加载试验亦可分为4 个主要步骤,前3 个步骤与上述的三轴固结排水剪切试验相同。完成前3 个步骤后,对试样进行轴向加载-卸载-再加载。初次所加荷载为试样预计破坏偏应力的40%,当荷载加至目标值时,马上进行轴向卸载,至荷载为0,然后再进行轴向加载,所加荷载为试样预计破坏偏应力的60%。为方便地控制所加荷载的数值,此步骤的3 个过程均采用应力控制。同时,为了保证孔隙水有充足的时间排出,对于②2和⑤3层试样,初次加载和卸载的时间步长均为32 h,再加载的时间步长为46 h。对于③、④层试样,初次加载和卸载的时间步长均为36 h,再加载的时间步长为54 h。
4.2.3 标准固结试验步骤
固结试验的主要步骤为给试样施加不同等级的荷载。试验采用5 级荷载,分别为50、100、200、400、800 kPa。每级荷载固结稳定时间取为24 h。
5 试验结果与参数确定
5.1 标准固结试验结果与参数确定
各土层标准固结试验所加荷载与试样轴向应变的关系曲线如图4 所示。试样孔隙比与所加荷载的关系曲线如图5 所示。
从图4 可以看出,各试样的轴向变形随着荷载的增加而增加,③、④两层土试样的轴向变形量明显大于②2、⑤3层。从图5 可以看出,各试样的孔隙比随着荷载地增大而减小,③、④两层土试样的初始孔隙比较大,孔隙比变化范围也大于②2、⑤3土层。

图4 各土层试样固结试验荷载-应变关系曲线图 Fig.4 Relationships between load and strain of consolidation test
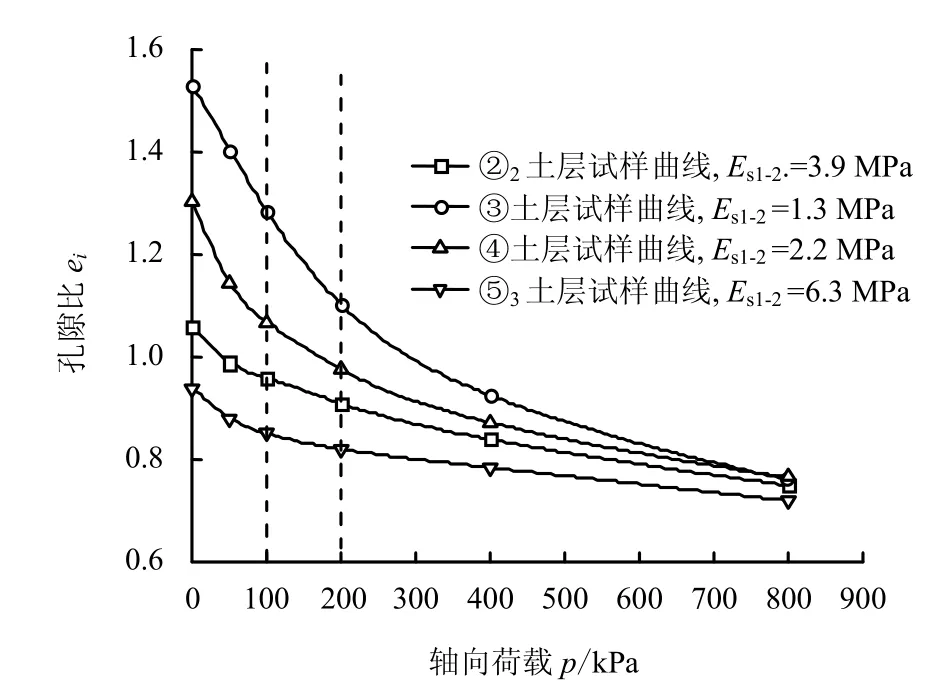
图5 各层试样固结试验孔隙比与荷载关系曲线图 Fig.5 Relationships between load and void ration of layers in consolidation test
将各土层试样的荷载-应变关系曲线拟合成函数关系表达式,如图4 所示,每条曲线的判定系数R2均为0.99。对函数求导可分别得到荷载p 为 100 kPa 时各曲线切线的斜率值,该值便是参考应力pref为100 kPa 时固结试验的参考切线模量。经计算,②2、③、④和⑤3土层的分别为:3.4、1.2、1.9、6.1 MPa。从图5 可得到各层试样荷载间隔p1=100 kPa 至p2=200 kPa 时对应的压缩模量Es1-2分别为3.9、1.3、2.2、6.3 MPa。
5.2 三轴固结排水剪切试验结果与参数确定
②2土层埋深较浅,三轴固结排水剪切试验所取的围压为70、100、200 kPa。其余土层所取的围压为100、200、300 kPa。围压100 kPa 下,②2、⑤3土层试样的应力-应变关系曲线如图6 所示;③和④土层试样的应力-应变关系曲线如图7 所示。
从图6 可以看出,②2、⑤3土层试样剪切初期偏应力随着应变的增加不断增加,应变增加至某一值时,应变再增加则应力保持不变或略有减小。按照土工试验方法标准[19],取轴向应变为15%的点所对应的偏应力值作为破坏值qf。连接原点和0.5qf所对应点的直线斜率即为试样的参考割线模量。因此,可得参考应力(此处即是围压) pref= 100 kPa 时,②2、⑤3土层试样的分别为4.4、5.5 MPa。另外,取曲线稳定段对应的偏应力值作为渐近值qa,可得②2、⑤3土层试样的破坏比R(fRf=qf/qa)分别为0.96、0.95。
从图7 可以看出,③、④土层试样偏应力随着应变的增加始终不断增加,偏应力没有峰值点,试样表现为应变硬化。取轴向应变为15%的点所对应的偏应力的值作为破坏值qf,经计算可得③、④土层试样的分别为1.6、2.0 MPa。根据Konder[20]的建议,将③、④土层试样的应力-应变曲线拟合成双曲线函数(R2=0.98),可得偏应力的渐近值qa,由此得到③、④土层试样的破坏比Rf分别为0.58、0.54。
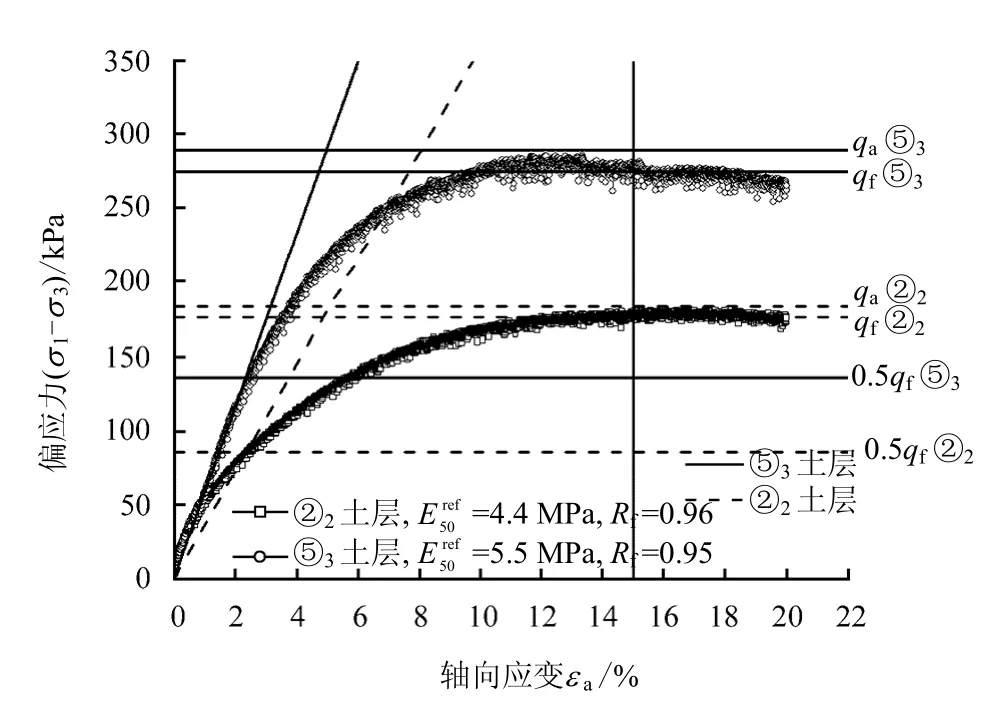
图6 ②2 和⑤3 土层试样三轴固结排水剪切试验 应力-应变关系曲线图 Fig.6 Strain-stress curves of triaxial CD test of layer ②2 and layer ⑤3

图7 ③和④土层试样三轴固结排水剪切试验 应力-应变关系曲线图 Fig.7 Strain-stress curves of triaxial CD test of layer ③ and layer ④
为了获得土体的有效黏聚力c′和有效内摩擦角φ′,各土层还进行了其他围压下的三轴固结排水剪切试验,各土层的应力摩尔圆如图8 所示。从图中可以发现,③层土摩尔圆不切于同一直线,原因是上海地区③层土为淤泥质粉质黏土,土质不均匀,所制备的3 个试样均有不同程度的夹砂现象,其中围压300 kPa 下的试样夹砂较其他围压下的试样严重,因此,该试样的强度大于相同围压下其他试样的强度。从摩尔圆可得到各层土的有效抗剪强度指标:②2土层土体的c′=10 kPa,φ′=25.2°;③层土的 c′=10 kPa, φ′ =20.1°;④层土的 c′=3 kPa,φ′=27.3°;⑤3层土的c′=20 kPa,φ′=26.7°。

图8 各土层试样应力摩尔圆 Fig.8 Mohr circle of each soil layer
5.3 三轴固结排水加载-卸载-再加载试验结果与参数确定
围压100 kPa 下,各层试样的三轴固结排水加载-卸载-再加载试验应力-应变关系曲线如图9 所示。

图9 各层试样三轴固结排水加载-卸载-再加载试验 应力-应变关系曲线图 Fig.9 Strain-stress curves of triaxial CD loading- unloading-reloading test of each layer
从图9 可以看出,在卸载-再加载过程中各土层试样的应力-应变关系均表现为一个滞回圈。卸载初期应力-应变曲线陡降,当减少到一定偏应力时,卸载曲线变缓,再加载,曲线开始陡而随后变缓。用卸载和再加载曲线的平均斜率,即连接滞回圈两端点的直线斜率[21],表示围压100 kPa 下试样的参考卸载再加载模量。②2、③、④和⑤3土层的分别为19.3、14.9、15.6 和23.5 MPa。
6 试验结果总结与对比
通过上海典型土层土样的三轴固结排水剪切试验、三轴固结排水加载-卸载-再加载试验以及标准固结试验可得到各土层的土体硬化模型参数:c′和φ′,参考应力100 kPa 下的、、和Rf,具体数值汇总见表2。
从表2 可以发现,上海软土地区软弱的③、④层土样的c′、φ′、、、、 Es1-2和破坏比Rf均小于⑤3、②2层土样。⑤3、②2两层土体的、和之间的比例关系基本相同。对于③、④层土,上述3 者之间的比例关系也较为接近。②2、③、④层土的值为压缩模量 1 2sE-的0.9倍,⑤3层土的值与s12E-相等。目前的勘察报告一般只提供s12E-,有了这些关系以后,就可以根据s12E-确定、和的值。

表2 土体硬化模型参数对比表 Table 2 Comparisons of parameters of the hardening soil model
为了对比,表中还给出了其他地区土体硬化模型的参数。从表2 亦可以发现,上海软土地区土体的有效黏聚力c′普遍大于表中其他地区土体,有效内摩擦角φ′与其他地区土体相当。③、④两层土体的破坏比Rf较小,②2、⑤3层土体的Rf与其他地区土体相近。上海软土的值为值的0.9~1.3倍,这与天津滨海软土[11]的0.5~1.8 倍、奥地利Lacustrine Clay[22]的1 倍以及美国Upper Blodgett[23]的1.5 倍比例关系相近,小于英国Gault Clay[24]的3.5 倍、台北Silty Clay[25]的2.8 倍,图10 清晰地反映了这一点。上海地区②2、⑤3层土体的值约为值的4.4 倍,这与Gault Clay 的3 倍、Taipei Silty Clay 的3 倍、Upper Blodgett 的4.3 倍和Lacustrine Clay 的4 倍都非常接近;③、④层土的值分别为值的9.3 倍和7.8 倍,该倍数关系大于其他地区土体,如图11。

图10 与 关系曲线图 Fig.10 Relationships between and

图11 与 关系曲线图 Fig.11 Relationships between and
7 结 论
(1)基于GDS 的三轴固结排水剪切试验、三轴固结排水加载-卸载-再加载试验以及标准固结试验测试了上海典型土层(②2、③、④、⑤3)土体HS模型参数中的c′、φ′、、、和Rf。这些参数可用于基坑开挖的数值分析。
[1] 上海市勘察设计行业协会, 上海现代建筑设计(集团)有限公司, 上海建工(集团)总公司. DG/TJ08-61-2010 基坑工程技术规范[S]. 上海: 上海市建筑建材业市场管理总站, 2010.
[2] 中国建筑科学研究院. JGJ 120-99 建筑基坑支护技术规程[S]. 北京: 中国建筑工业出版社, 1999.
[3] 陈晓平, 闫军. 深基坑支护结构的三维杆系有限元分析[J]. 岩土力学, 2001, 22(3): 258-261. CHEN Xiao-ping, YAN Jun. 3D pole system FEM analysis for bracing structure of deep foundation pit[J]. Rock and Soil Mechanics, 2001, 22(3): 258-261.
[4] 徐中华, 王建华, 王卫东. 主体地下结构与支护结构相结合的复杂深基坑分析[J]. 岩土工程学报, 2006, 28 (增刊): 1355-1359. XU Zhong-hua, WANG Jian-hua, WANG Wei-dong. Analysis of a complicated deep excavations supported by substructures[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(Supp.): 1355-1359.
[5] 应宏伟, 郭跃. 某梁板支撑体系的深大基坑三维全过程分析[J]. 岩土工程学报, 2007, 29(11): 1670-1675. YING Hong-wei, GUO Yue. 3D analysis on a deep beam-slab braced foundation pit considering effect of construction process[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(11): 1670-1675.
[6] 徐中华, 王卫东. 敏感环境下基坑数值分析中土体本构模型的选择[J]. 岩土力学, 2010, 31(1): 258-264. XU Zhong-hua, WANG Wei-dong. Selection of soil constitutive models for numerical analysis of deep excavations in close proximity to sensitive properties[J]. Rock and Soil Mechanics, 2010, 31(1): 258-264.
[7] SCHWEIGER H F, VERMEER P A, WEHNERT M. On the design of deep excavations based on finite element analysis[J]. Geomechanics and Tunnelling, 2009, 2: 333-344.
[8] BLACKBURN J T. Automated remote sensing and three dimensional analysis of internally braced excavations[D]. Evanston: Northwestern University, 2005.
[9] FINNO R J, CALVELLO M. Supported Excavations: Observational method and inverse modeling[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2005, 131(7): 826-836.
[10] CALVELLO M, FINNO R J. Selecting parameters to optimize in model calibration by inverse analysis[J]. Computers and Geotechnics, 2004, 31(5): 411-425.
[11] 刘畅. 考虑土体不同强度与变形参数及基坑支护空间影响的基坑支护变形与内力研究[D]. 天津: 天津大学, 2008.
[12] SCHANZ T, VERMEER P A, BONNIER P G. The Hardening Soil model: formulation and verification[C]// Beyond 2000 in Computational Geotechnics—10 years of PLAXIS. Amsterdam: [s. n.], 1999: 281-296.
[13] BRINKGREVE R B J. Selection of soil models and parameters for geotechnical engineering application[C]// Proceedings of Geo-Frontier Conference. Texas: Soil Properties and Modeling Geo-Institute of ASCE, 2005: 69-98.
[14] 黄绍铭, 高大钊. 软土地基与地下工程(第二版)[M]. 北京: 中国建筑工业出版社, 2005.
[15] GAO D Z, WEI D D, HU Z X. Geotechnical properties of Shanghai soils and engineering applications[M]// CHANEY RONALD C. Marine Geotechnology and Nearshore/offshore Structures. Philadelphia: ASTM, 1986: 161-178.
[16] JANBU J. Soil compressibility as determined by oedometer and triaxial tests[C]//Proceedings of the 3rd European Conference on Soil Mechanics and Foundation Engineering. Wiesbaden: [s. n.], 1963.
[17] BRINKGREVE R B J, BROERE W. Plaxis material models manual[M]. Delft: [s. n.], 2006.
[18] BOLTON M D. The strength and dilatancy of sands[J]. Géotechnique, 1986, 36(1): 65-78.
[19] 南京水利科学研究院. GB/T50123-1999 土工试验方法标准[S]. 北京: 中国计划出版社, 1999.
[20] KONDER R L. Hyperbolic stress-strain response: cohesive soils[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1963, 89(1): 115-143.
[21] 李广信. 高等土力学[M]. 北京: 清华大学出版社, 2004.
[22] LÜFTENEGGER R, SCHWEIGER H F, SCHARINGER F. 3D finite element analysis of a deep excavation and comparison with in situ measurements[M]//Geotechnical Aspects of Underground Construction in Soft Ground, London: Taylor & Francis Group, 2009: 193-199.
[23] ROBOSKI J F. Soil parameters for constitutive models of compressible Chicago glacial clays[D]. Evanston: Northwestern University, 2001.
[24] NG C W W. An evaluation of soil-structure interaction associated with a multi-propped excavation[D]. Bristol: University of Bristol, 1992.
[25] OU C Y, SHIAU B Y, WANG I W. Three-dimensional deformation behavior of the Taipei National Enterprise Center (TNEC) excavation case history[J]. Canadian Geotechnical Journal, 2000, 37(2): 438-448.
——结构相互作用的影响分析

