岩石节理倾角和间距对隧道掘进机破岩 特性影响的试验研究

邹 飞 ，李海波周青春莫振泽朱小明牛 磊杨风威

（1. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071； 2. 贵州省质安交通工程监控检测中心有限责任公司，贵阳 550000）

1 引 言

岩石节理特征是影响TBM（隧道全断面掘进机）滚刀破岩性能的重要因素之一。针对这一问题，国内外学者进行了大量的相关研究[1－6]，例如，美国科罗拉多矿业学院（Colorado School of Mines，CSM）通过巴西盘抗拉强度试验，获得岩石层理与加载方向不同夹角时的抗拉强度，以此来分析TBM 滚刀侵入方向与岩石层理面方向之间的关系对TBM 掘进性能的影响。挪威科技大学（NTNU）则根据岩体中裂隙、节理之问的间距将其分为5 类，用裂隙因子SK（裂隙和节理类别以及弱面与隧道轴线之间的夹角的函数）来评价裂隙和节理对TBM掘进性能的影响，并建立数据库和预测模型对实际工程的掘进进行有效的预测和指导。

龚秋明[7－8]通过离散元软件UDEC 对TBM 滚刀破岩过程进行了数值模拟，结果表明，节理间距、方向对岩石破碎过程中的裂纹扩展模式有着明显的影响。龚秋明等[9]还研究了锦屏Ⅱ级引水隧道工程中，大理岩的层厚对TBM 破岩效果和施工进度的影响，研究发现，薄层岩体在滚刀下容易形成完全贯穿岩层的裂纹而形成大块岩体，掌子面容易失稳，中层只有靠近层面才类似薄层，而厚、巨厚层岩体受岩层的影响较小，属于正常破岩。

Howarth[10]通过线性切割试验研究了岩体中存在一组节理时节理的间距对破岩效果的影响，试验结果表明，在贯入相同深度时，节理间距越小，贯入所需轴向推力越小。Wanner[11]通过现场调查研究认为，含软弱夹层的张性节理能明显的提高钻掘效率，其钻掘速率将比一般平均掘进速率高50%～100%。

本文通过压头的贯入破坏试验探讨岩石节理的间距和方向对压头贯入荷载的影响，并研究不同节理倾角和间距条件下试件表面裂纹的演化模式，旨在为TBM 隧道掘进参数确定提供参考。

2 压头贯入破坏试验

2.1 试件材料的选取及其准备

为了使所选材料有致密的结构和较小的孔隙率，试验试件采用α 型高强石膏浇注。高强石膏晶粒较粗，比表面积比较小，调成石膏浆体的可塑需水量很小，硬化后孔隙率小、强度高，使得试件有较高的弹性模量及抗压强度，并具有显著的脆性特征。具体参数如下表1 所示

表1 材料物理力学参数 Table 1 Physico-mechanical parameters of materials

为使试件所产生的尺寸效应不受到侧向自由边界的影响[12]，试件尺寸采用150 mm×150 mm× 20 mm（长×宽×高）。为了保证试件力学性质的一致性，所有试件均采用同一批次高强石膏。试件采用特制的铝质模具进行浇注。模具内部涂专用脱模剂，使试件脱模后的表面有很高的平整度。浇注之前在模具中插0.3 mm 的薄钢片，浇注以后在试件初凝前抽出，利用石膏的热膨胀性，使得裂隙闭合形成节理。

2.2 试验的加载以及数据采集系统

试验采用120°角的楔形压头，刃口的长度为 40 mm，刃宽为3 mm。试验在经过改装的RMT-150C型岩石力学试验系统上进行。试件的两侧用侧向千斤顶通过刚性承压板施加一定围压来提供约束。模拟TBM 侵入力的法向荷载由试验机提供，试验中把压头的中心部分和试件的中心对齐，避免轴向荷载的偏心。试验过程中侵入深度通过位移传感器测量，法向荷载通过安装在轴向伺服千斤顶上的压力传感器测量。加载过程中，用CCD 相机采集试件表面裂纹扩展图像。试验装置如图1 所示：

图1 试验装置 Fig.1 Test equipment

2.3 试验方案

试验中采用4 种节理倾角和5 种不同的节理间距，试验模型如图2 所示。图中D 代表节理的间距，α 代表节理面与压头贯入平面（TBM 开挖中的掌子面所处平面）的夹角，当节理为水平即α =0°时，表示压头与试件接触点到节理面的间距。考虑到试件尺寸和边界效应，具体参数如表2 所示。

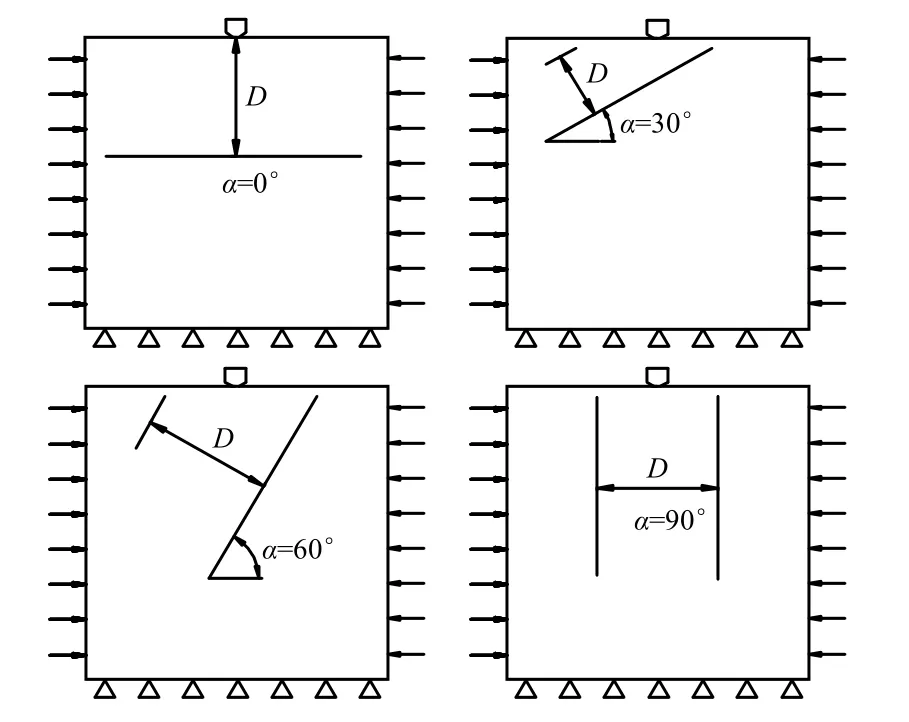
图2 试验模型 Fig.2 Test models

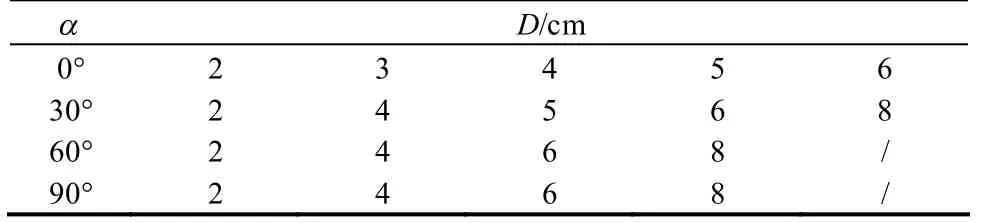
表2 试件节理参数 Table 2 Joint parameters of specimens

3 试验结果及其分析

3.1 不同节理倾角和间距情况下贯入荷载-侵深曲线特征

图3～6 为不同节理倾角和间距条件下，压头贯入过程中的荷载－侵深曲线，荷载所反映的是试件对压头贯入过程中的抵抗力，侵深则是压头贯入试件中的深度。其基本特征为：在加载初期，荷载与侵深成比例增加，当荷载持续增加达到跃进点（荷载跌落之前达到的最大值，图中虚线所示位置）后，主裂纹迅速扩展，荷载明显跌落，且跌落速率相当快，该特征说明主裂纹扩展的突发性。

图7 反映的是不同节理倾角情况下跃进点荷载与节理间距的关系，可以看出，当节理倾角一定时，节理间距越大，达到跃进点的贯入荷载值越大。

跃进点荷载与节理倾角的关系如图8 所示，为了进行有效对比，选择不同节理角度下节理间距相同的3 种工况进行分析，其基本规律为：在相同节理间距条件下，随着节理倾角的增加其跃进点荷载都呈先减小后增大的趋势，当α 为30°时，所需荷载值最小。

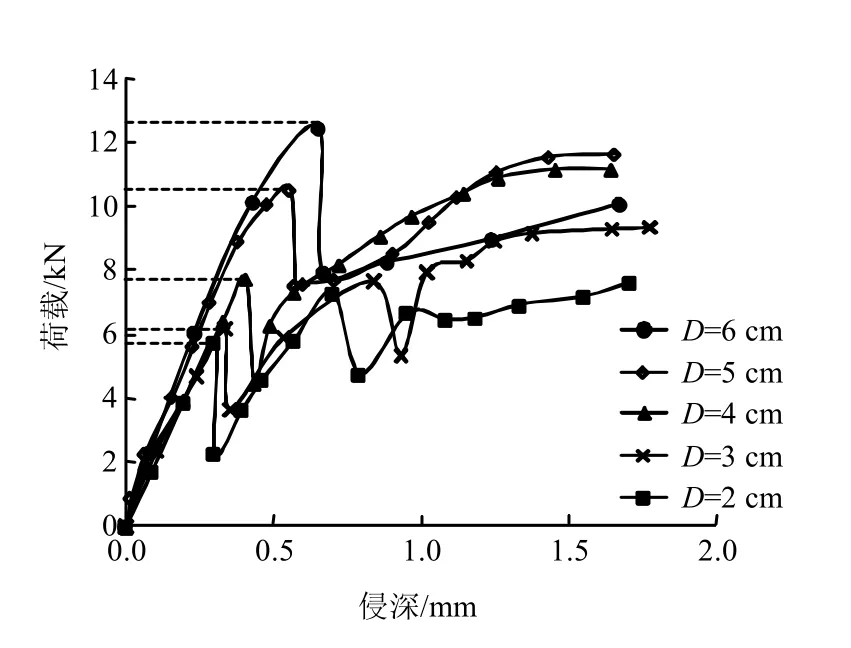
图3 α =0°时荷载-侵深曲线 Fig.3 Load-penetration depth curves atα =0°

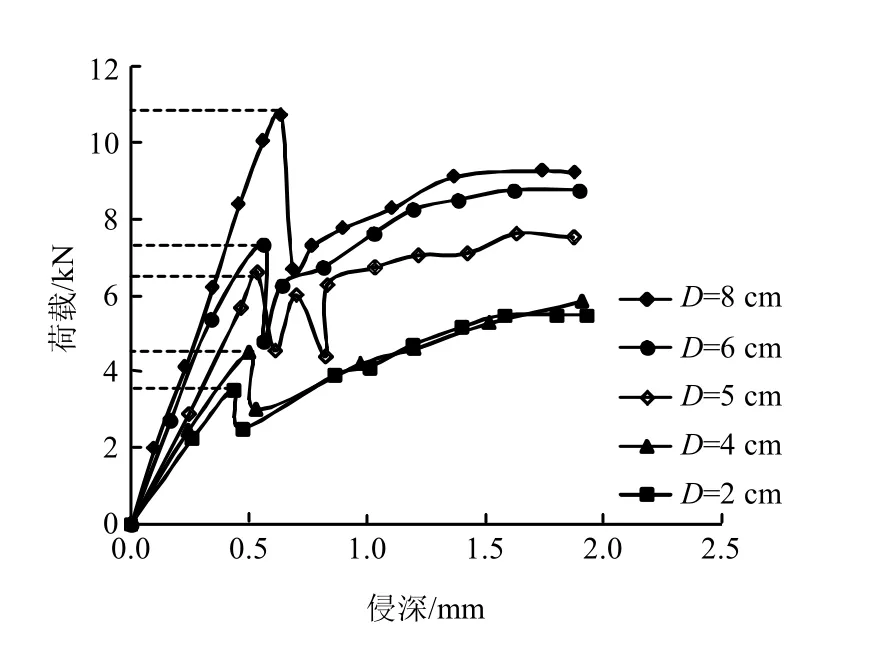
图4 α =30°时荷载-侵深曲线 Fig.4 Load-penetration depth curves atα =30°

图5 α =60°时荷载-侵深曲线 Fig.5 Load-penetration depth curves atα =60°

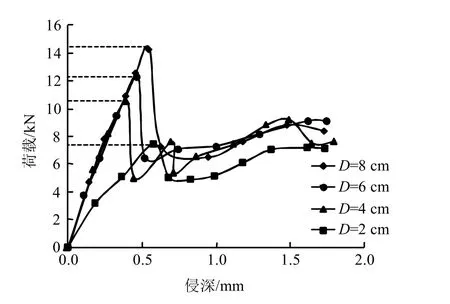
图6 α =90°时荷载-侵深曲线 Fig.6 Load-penetration depth curves atα =90°

图7 节理间距与跃进点荷载关系 Fig.7 Relationships between joint space and peak load

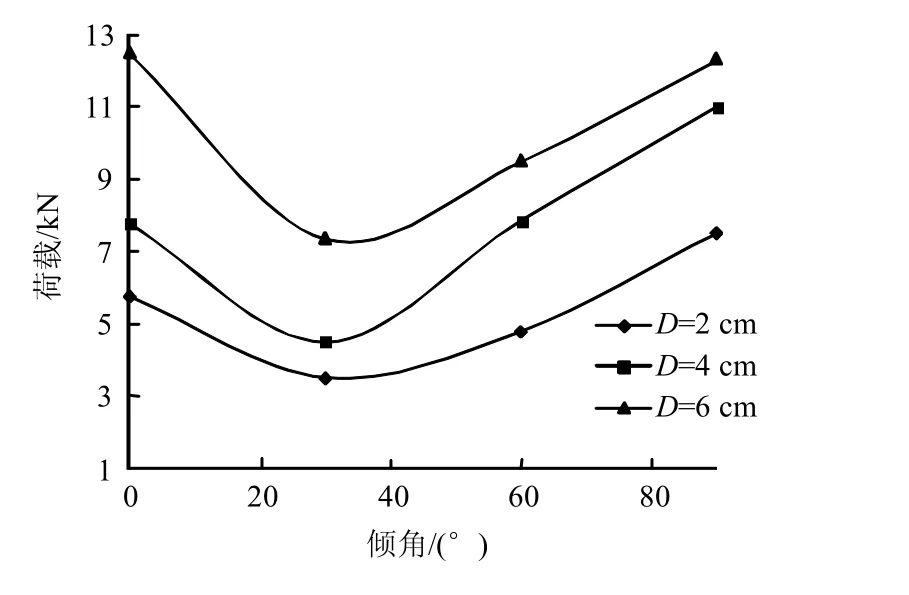
图8 节理倾角与跃进点荷载关系 Fig.8 Relationships between joint angle and peak load

3.2 不同节理倾角和间距情况下侵入特征

荷载－侵深曲线所反映的是压头下粉碎区、塑 性区的发展导致试件局部区域刚度弱化以及弹性 区域的变形的综合表现，曲线特征反应了岩石抗侵入的能力。用文献[13-14]中定义的抗侵入系数K（kN∙mm-1），即侵入单位深度所需荷载对曲线特征进行表述，具体定义为

式中：P 为跃进点荷载（kN）；U 为跃进点刀具贯入深度（mm）。

侵入功A（kN∙mm）所反应的是试件从加载到主裂纹扩展形成荷载跌落整个过程所消耗的能量，即图9 中 OAUΔ 面积，其表达式为：

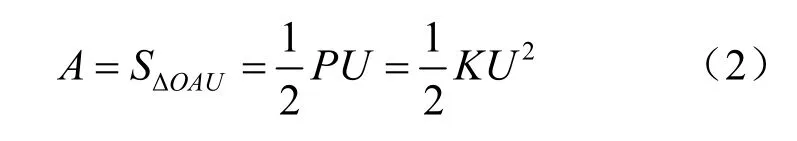
由于荷载的跌落与主裂纹的扩展有关，建立主裂纹扩展与能量释放之间的关系： 裂纹扩展所需要的能量E（kN∙mm）为图9 中 OABΔ 的面积。

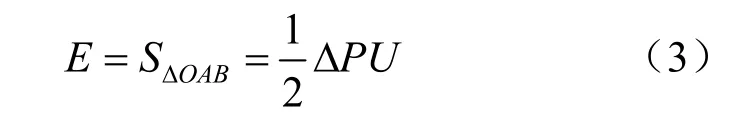
根据试验得到的荷载－侵深曲线，得到不同节理倾角和间距条件下的K、A、E 值的统计见表3。

K、A、E 值的基本变化规律为：节理倾角一定时，节理间距越大，岩石的抗侵入系数越大，达到跃进破碎时所需侵入功越多，裂纹扩展所需能量越大。具体分析如下：

不同节理倾角下，节理间距对K 值的影响如图10 所示：（1）α = 0°时，压头下应力场呈对称分布。在达到跃进点之前，5 种不同节理间距试件的抗侵入系数基本一致，都在19 左右，可见水平节理对抗侵入系数的影响很小。（2）α = 30°时，压头到节理面的垂直距离从1 cm 增加到4 cm，抗侵入系数呈逐渐增大趋势，最小值为8.14，最大值为17.06，节理倾角的变化对试件抵抗侵入的能力产生明显的影响，节理间距越小抗侵入系数越小。（3）α = 60°时，压头到节理面的垂直距离从1 cm 增加到4 cm，抗侵入系数呈逐渐增大趋势，D = 8 cm 时抗侵入系数与D = 6 cm 时的抗侵入系数基本一致，表明在该节理角度下节理间距超过一定的值，对K 值影响明显降低。（4）α = 90°时，D = 2 cm 时，K 值为12.91。当D 增加到4、6、8 cm 时，K 值分别为25.00、26.19、26.00，K 值的变化波动不大，基本一致。

不同节理倾角下，节理间距对侵入功A 以及主裂纹扩展所需能量E 的影响如图11、12 所示。A、E 值的变化规律为：在达到跃进点之前，节理间距越大，所需侵入功越多，裂纹扩展所需能量越大。除D = 2 cm，α = 90°外，其余工况下侵入功与节理间距线性相关，主裂纹扩展所需能量是关于节理间距的幂函数。

不同节理间距下，节理倾角对A、E、K 值的影响如图13～15 所示。其基本规律为：在相同节理间距条件下，随着节理倾角的增加，A、E、K 值都呈先减小后增大的趋势，在α = 30°时，A、E、K 值最小。

α = 90°时，裂纹扩展模式与其他角度不相同，对抗侵入系数、侵入功以及主裂纹扩展所需能量的影响有着本质的区别，在此进行说明：由于节理与贯入方向平行，侧向裂纹的扩展被节理限制，不能有效扩展，增加了抵抗压头贯入的能力。中间主裂纹则是从压头端部起裂，向试件内部扩展，所受约束越来越大，其他角度则是从节理面处起裂，向压头端部发展，所受约束越来越小。尤其是D = 2 cm，由于节理间距偏小，侧向裂纹的扩展被节理所限制，导致压头下应力集中，材料过度破碎，使得K 值偏小、A 值则偏大，由于该工况的特殊性，在图10、11 中用圆圈标识。

图9 荷载-侵深曲线 Fig.9 Load-penetration depth curves

表3 K、A、E 值的统计 Table 3 Statistics of the value of K, A and E

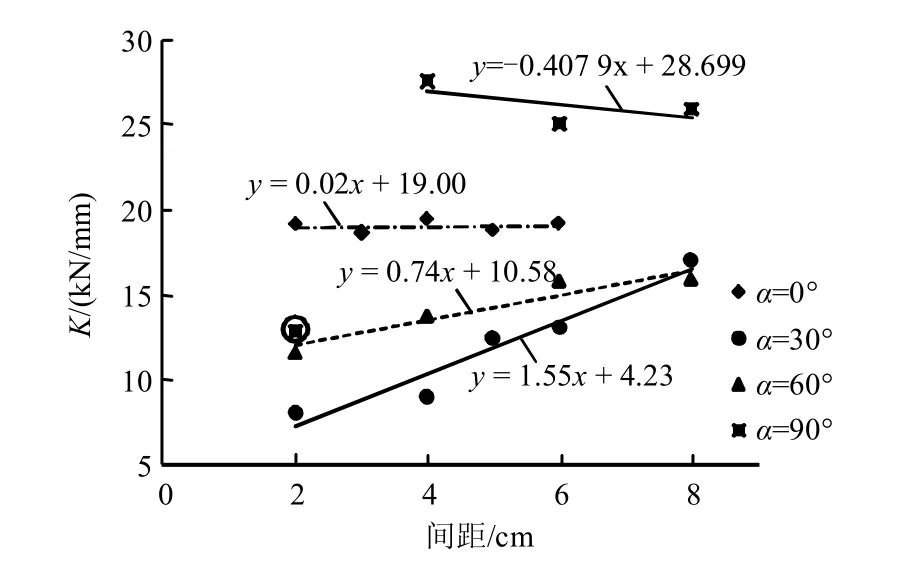
图10 节理间距与K 值关系 Fig.10 Relationships between joint space and values of K

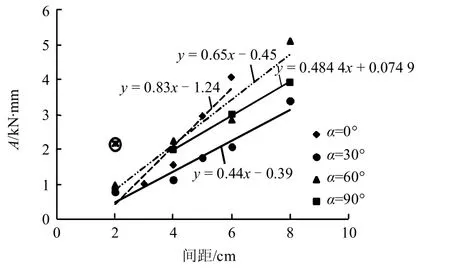
图11 节理间距与A 值关系 Fig.11 Relationships between joint space and values of A

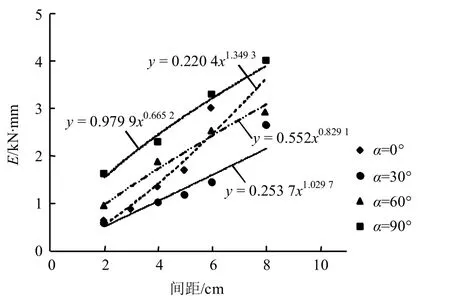
图12 节理间距与E 值关系 Fig.12 Relationships between joint space and values of E

图13 节理倾角与K 值关系 Fig.13 Relationships between joint angle and values of K

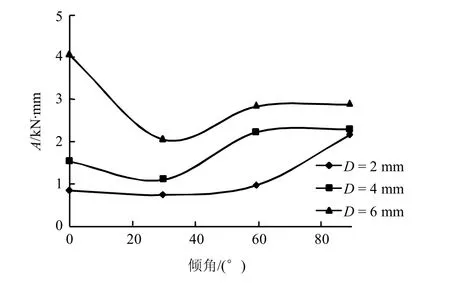
图14 节理倾角与A 值关系 Fig.14 Relationships between joint angle and values of A

图15 节理倾角与E 值关系 Fig.15 Relationships between joint angle and values of E

3.3 不同节理倾角和间距情况下试样破坏特征

图16 为不同节理倾角和间距条件下试样破坏区域的裂纹素描图，虚线表示节理，实线表示宏观裂纹。试件编号约定：节理间距+节理倾角，为了体现裂纹细节各图比例尺未进行统一，以间距D 的长度体现。如2-30 表示节理间距D 为2 cm，节理倾角为30°。当节理倾角为0 时，D 表示节理到压头的距离。

从图16 可以看出：节理的空间位置对裂纹的扩展有着明显的控制作用，节理面既是拉破坏裂纹的起裂位置，同时也对裂纹的扩展起到了阻隔作用。节理面平行或垂直贯入方向时，裂纹空间分布近似对称，当呈一定角度时，裂纹则发生大的偏转。具体分析如下：

（1）α = 0°时：在刀具荷载作用下，试件所受力呈对称分布，由于节理的水平分割，节理面上与侵入方向相交点的拉应力迅速集中，当节理间距偏小时，首先达到抗拉极限，裂纹起裂，并迅速向压头端部扩展。

D = 2 cm 时，环形裂纹所包围的破坏剥离区仅限于压头与节理之间部分，中间拉裂纹首先从节理面上表面起裂向压头端部扩展，随后在节理面下表面起裂向试件内部发展。

D = 3、4、5 cm 时，发育明显的侧向裂纹以及环形裂纹，两2 条中间裂纹近似平行发展。其顺序为：中间裂纹首先从节理面向压头扩展，在密实核边缘终止，随后刀头两侧出现明显的侧向裂纹。

D = 6 cm 时，中间裂纹从压头向节理扩展，随后出现环形裂纹，最后出现侧向裂纹，最终裂纹扩展贯通导致破碎块体剥离。

（2）α = 30°时：节理的存在破坏了应力场的对称性，差异变形引起的拉应力在节理面处垂直于微裂隙表面，并使裂纹尖端产生大的拉应力场，随着荷载的增加，裂纹失稳扩展。

D = 2 cm 时，共出现3 条主裂纹，其中一条的起裂点位于节理面上，且该点为节理到压头距离最近点，裂纹近似垂直于节理。侧向裂纹扩展到一定程度后发生明显的偏转，平行节理方向继续扩展。D = 4 cm 时与D = 2 cm 时基本相似，只是侧向裂纹未发生偏转，扩展到节理处终止。

D = 5 cm 时，除环形裂纹以及垂直节理面并扩展到压头的一条裂纹外，在压头下部处发育3 条明显侧向裂纹，2 条扩展到节理面处终止，另外1 条平行节理方向扩展，其末端发育垂直节理面的次级裂纹。

图16 试件破坏后裂纹扩展素描图 Fig.16 Crack sketches of the damage specimens

D = 6、8 cm 时，基本一致，压头下部由剪切破坏形成的环形裂纹，并伴随有少量次生裂纹以及1 条从节理面到密实核边缘的拉裂纹。

（3）α = 60°时：D = 2 cm 时，由于节理间距偏小，限制了裂纹的扩展，导致压头下小区域内裂纹数量明显偏多，发育多条侧向裂纹，同时发育1 条中间裂纹平行节理方向扩展。

D = 4、6、8 cm 时，裂纹发育形态基本一致，除部分次级裂纹以外，主裂纹发育规律如下：1 条由节理面处扩展到压头的裂纹，1 条从压头下部的密实核区域边缘扩展的中间裂纹，该裂纹的最大特点是扩展方向逐渐平行节理方向。

（4）α = 90°时：试件所受力呈对称分布，节理对侧向裂纹的扩展有明显的控制作用，对中间裂纹的影响则较小。D = 2、4、6 cm 时，侧向裂纹终止于节理面处，中间裂纹张性明显。D = 8 cm 时，除环形裂纹和侧向裂纹发育外，中间裂纹开始扩展就出现大的偏转，可能是试件受力不对称，导致差异变形造成的。

4 结 论

（1）当节理倾角一定时，随着节理间距增大，达到跃进点的贯入荷载值增加，侵入功以及主裂纹扩展能量也都呈增大趋势。α =0°、90°时，抗侵入系数基本一致（除α =90°，D = 2 cm 时，抗侵入系数明显偏低），α = 30°、60°时，抗侵入系数呈增大趋势。

（2）当节理间距一定时，随着α 角度的增加，跃进点荷载、抗侵入系数、侵入功以及主裂纹扩展能量都呈先减小后增大趋势。在α = 30°时，各值都为其最小值，即节理面与侵入方向的夹角为60°时，最有利于刀具破岩，该工况下TBM 的掘进速率能有效提高

（3）节理面的空间位置控制着压头下试件的变形及破坏过程，节理面有利于拉裂纹的起裂，但同时又对裂纹的扩展起到了阻隔作用，当节理面平行或垂直贯入方向时，裂纹扩展分布近似对称，当呈一定角度时，裂纹则发生大的偏转。

实际工程表明，节理对TBM 掘进速率有着重要影响。本文通过试验研究节理面参数对抗侵入系数、侵入功以及主裂纹扩展能量的影响，对指导TBM 在节理岩体隧道施工中采取合理掘进参数有着一定的参考意义。

[1] 龚秋明， 赵 坚， 张喜虎. 岩石隧道掘进机的施工预测模型[J]. 岩石力学与工程学报， 2004， 23(增刊2)： 4709－4714. GONG Qiu-ming， ZHAO Jian， ZHANG Xi-hu. Performance prediction of hard rock TBM tunneling[J]. Chinese Journal of Rock Mechanics and Engineering， 2004， 23(Supp.2)： 4709－4714.

[2] ROSTAMI J. Development of a force estimation model for rock fragmentation with disc cutters through theoretical modeling and physical measurement of crushed zone pressure[D]. Colorado： Colorado School of Mines， 1997.

[3] ROSTAMI J， OZDEMIR L， NILSEN B. Comparison between CSM and NTH hard rock TBM performance prediction models[C]//Proceedings of Annual Technical Meeting of the Institute of Shaft Drilling and Technology (ISDT). Las Vegas： [s. n.]， 1996.

[4] ROSTAMI J， OZDEMIR I. A new model for performance prediction of hard rock TBMs[C]// Proceedings of Rapid Excavation and Tunneling Conference. Boston： [s. n.]， 1993： 793－809.

[5] NELSON B， OZDEMIR L. Hard rock boring performance and field performance[C]//Proceedings of Rapid Excavation and Tunneling Conference. [S. l.]： [s. n.]， 1993： 833－852.

[6] 徐则民， 黄润秋， 张倬元. TBM 刀具设计中围岩力学参数的选择[J]. 岩石力学与工程学报， 2001， 20(2)： 230－234. XU Ze-min， HUANG Run-qiu， ZHANG Zhuo-yuan. The mechanical parameters of surrounding rocks considered in TBM cutter design[J]. Chinese Journal of Rock Mechanics and Engineering， 2001， 20(2)： 230－234.

[7] GONG Qiu-ming， ZHAO Jian， JIAO Yu-yong. Numerical modeling of the effects of joint orientation on rock fragmentation by TBM cutters[J]. Tunnelling and Underground Space Technology， 2005， (20)： 183－191.

[8] GONG Q M， JIAO Y Y， ZHAO J. Numerical modeling of the effects of joint spacing on rock fragmentation by TBM cutters[J]. Tunnelling and Underground Space Technology， 2006， (21)： 46－55.

[9] 龚秋明， 佘祺锐， 王继敏， 等. 不同层厚层状岩体对TBM 开挖的影响[J]. 岩石力学与工程学报， 2010， 29(7)： 1442－1449. GONG Qiu-ming， SHE Qi-rui， WANG Ji-min， et al. Influence of different thicknesses of marble layers on TBM excavation[J]. Chinese Journal of Rock Mechanics and Engineering， 2010， 29(7)： 1442－1449.

[10] HOWARTH D F， ROWLANDS J C. Quantitative assessment of rock texture and correlation with drillability and strength properties[J]. Rock Mechanics and Rock Engineering， 1987， 20(1)： 57－85.

[11] WANNER H. On the influence of geological conditions at the application of tunnel boring machines[J]. Bulletin of Engineering Geology and the Environment， 1975， 12(1)： 21－28.

[12] 陈立宪， 黄国忠， 陈尧中. 岩体贯切破坏在不同侧向自由边界的声发射演化[J]. 岩石力学与工程学报， 2009， 28(12)： 2411－2420. CHEN Li-hsien， HUANG Kuo-chung， CHEN Yao-chung. Acoustic emission evolution in indentation fracture of rocks under different lateral stress-free boundaries[J]. Chinese Journal of Rock Mechanics and Engineering， 2009， 28(12)： 2411－2420.

[13] 徐小荷， 余静. 岩石破碎学[M]. 北京： 煤炭工业出版社， 1984.

[14] 李国华， 陶兴华. 动、静载岩石破碎比功实验研究[J]. 岩石力学与工程学报， 2004， 23(14)： 2448－2454. LI Guo-hua， TAO Xing-hua. Testing study on crushing working ratio of rock under dynamic and static loads[J]. Chinese Journal of Rock Mechanics and Engineering， 2004， 23(14)： 2448－2454.