我国农业全要素生产率增长及收敛研究
张海波,刘 颖
(华中农业大学 经济管理学院,湖北 武汉 430070)
0 引言
2011年我国粮食总产量与去年相比增长4.52%,粮食产量实现了从2004~2011年连续8年增长。粮食产量的持续增长,一方面是由于农业生产要素投入的增加,另一方面是由于农业科学技术的进步和生产效率的改善,农业全要素生产率(TFP)的提高。依靠增加农业生产要素投入而带动产出增长,这种增长方式不具有可持续性;只有依靠农业科学技术,才能带来农业产出的持续增长。改革开放以来,我国农业机械化水平不断提高,农业科学技术有了很大的进步,农业TFP也一直处于上升趋势。但目前我国农业发展水平还存在着比较明显的地区差异,不同地区农业TFP的增长速度各不相同,如果农业生产率较低地区的TFP增长速度快,那么地区间的农业发展水平差距将逐渐缩小,农业TFP增长出现收敛趋势;反之,如果地区间的差距越来越大,那么则出现发散趋势。
关于我国不同地区的农业TFP是否出现了收敛趋势的这一问题,已经引起很多学者的关注与研究。从现有的研究可以看出,大多数学者在计算TFP时都选择了非参数法中Malmquist指数法,因为非参数法不需要设定具体的函数形式,不需要严格的假定,也不需要进行假设检验,计算过程较为简便。虽然这些学者在测算TFP时充分考虑了随机因素的影响,计算结果能够相对客观的反映实际情况,但他们并没有对计算得到的农业TFP是否存在σ收敛和β收敛进行分析。由于考虑随机因素影响后的结果更能反映实际情况,所以本文在测算我国1980~2009年的农业TFP时采用SFA方法,在此基础上对计算得到的结果进行收敛性分析,以确定我国农业TFP是否存在σ收敛和β收敛趋势。
1 随机前沿分析与全要素生产率
1.1 理论与研究方法
本文采用Battese和Coelli(1995)[13]提出的计算生产效率的方法,该方法考虑了随机因素对结果的影响,并将技术无效率的分布均值表示为效率影响因素的函数,在估计生产函数的同时可以估计出技术无效率函数。随机前沿分析的基本模型为:
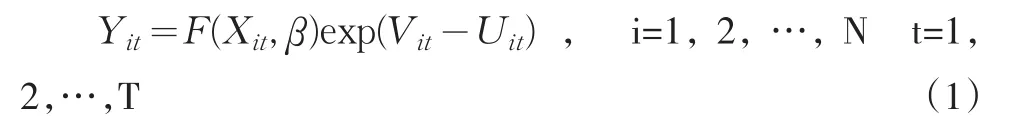
其中,F(Xit,β)表示已经设定的具体生产函数形式,Yit表示个体i在t时期的产量;Xit是个体i在t时期的K×1维要素投入;β是待估参数;Vit是随机扰动项,表示诸如天气、自然灾害、努力程度和运气等,服从正态分布N(0,σv2)并独立于技术无效率变量Uit;Uit是非负随机变量,表示生产效率的无效程度,反映个体的实际产出与生产前沿的差距,假设服从非负截尾正态分布N(mit,σu2),并同时假设mit=zitδ,zit为P×1维的向量,表示影响个体效率的因素,P为影响因素的数量;δ为待估参数向量;另外,σ2=(σv2+σu2),γ=σu2/(σv2+σu2),当γ趋于1时,表明个体的实际产出与生产前沿的差距主要来源于技术无效率的影响;当γ趋于0时,表明差距主要来源于统计误差或随机变量的影响。
技术效率用个体i在t时期存在技术无效率时的实际产出与个体i在t时期技术完全有效时的产出的比值来确定,那么个体i在t时期的技术效率可以用公式(2)的函数形式来表示,所以技术效率的变化率(TEC)可以表示为:TEC=-dU/dt。

将对数形式的前沿生产函数对时间t求导数,可得:

其中,等式右边的第一项代表技术进步(TP),反映在保持投入要素不变的情形下,前沿生产技术进步导致的前沿产出随时间趋势的增长率;第二项代表在既定技术水平的情况下,投入要素变化所引起的前沿产出随时间趋势的变化率。要素Xj变化率的表达式为:
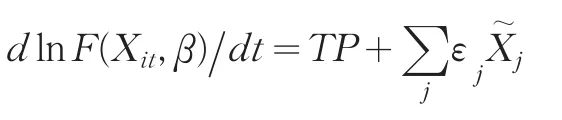
将表达式(1)转化为对数形式,然后等式两边对时间t进行全微分,假设不考虑随机误差项,并令产出增长率,通过整理后得到如下的表达式:

1.2 建立模型、数据处理与实证分析
本文选用超越对数生产函数,因为其放宽了Cobb-Douglas生产函数中的技术中性、产出弹性固定的假设,当对一些具体条件进行约束时可以得到多种生产函数的近似。因此本文首先以超越对数生产函数形式为基础对模型进行估计,在此基础上进行各种检验,最后选择合适的生产函数形式。本文经过比较,最终选择的生产函数形式为:

技术无效率函数的形式为:
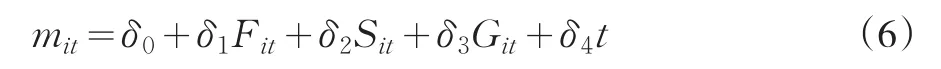
本文选择的样本为我国30个省市自治区①为了保持统计数据口径的一致,本文中的四川包括重庆。1980~2009年的农业生产数据②由于部分数据缺失,本文通过做自身回归分析而得到。,数据来源于《新中国60年统计资料汇编》和国泰安数据服务中心。本文的产出量用农林牧渔业总产值表示,并以1980年的价格水平为基准对以后各期的农林牧渔业总产值进行调整,用Y表示;用农业机械总动力和第一产业从业人员分别代表资本和劳动的投入,用K和L表示;本文认为农业生产活动的效率主要受化肥施用量、农作物总播种面积和有效灌溉面积的影响,分别用F、S、G表示;t表示时间变量。我国1980~2009年的农业生产数据的描述性统计见表1。

表1 我国各地区农业产出与投入的描述性统计
本文采用极大似然估计方法对生产函数和效率函数进行估计,参数估计结果见表2③表2结果由计量软件Frontier Version 4.1估计得到。。由表2可知,绝大多数估计值在1%的水平上具有显著性。农业机械总动力和和第一产业从业人员之间的替代弹性为0.1875;γ的值为0.79928,这就意味着我国各地区农业生产中20.07%的技术无效率是由随机因素引起的,79.93%的技术无效率是由是由化肥施用量、农作物总播种面积和有效灌溉面积因素引起的,这三个变量的估计值显著为负值,说明在现有的技术条件下,增加化肥施用量、扩大农作物总播种面积和有效灌溉面积可以提高农业生产的技术效率。时间变量的估计值为0.03979,说明改革开放以来,我国农业生产的技术效率在不断降低,农业TFP的提高主要是由技术进步引起的。

表2 参数估计结果及相关统计量
随机前沿分析的结果在很大程度上依赖于设定的函数形式,函数形式正确与否会直接影响到结论的可靠性。为了保证函数(5)和(6)的适当性,本文针对表2的估计结果做了4个方面的假设检验:(1)技术非效率项是否存在的检验;(2)技术变化是否存在的检验;(3)技术进步是否是希克斯中性的检验;(4)Cobb—Douglas生产函数是否适用的检验。
根据Battese和Coelli(1995)[1]的研究,函数设定中所涉及的假设都可以使用广义似然率统计量(LR)来进行检验,LR统计量的具体形式为:LR=-2[L(H0)-L(H1)],其中,L(H0)表示零假设(H0)条件下的似然函数对数值,L(H1)表示备择假设(H1)条件下的似然函数对数值,通常认为LR统计量近似服从卡方分布或混合卡方分布,如果零假设中包含了γ=0,那么统计量LR就服从混合卡方分布。如果LR>χ2(k),那么就拒绝零假设,其中k代表自由度即约束条件的个数。由表3中可以看出,所有的检验统计量都大于相应的临界值,零假设均被拒绝。这表明本文所设定的超越对数生产函数形式是适当的,包含技术无效率项的函数形式可以较好的反映我国农业各地区的农业生产状况。
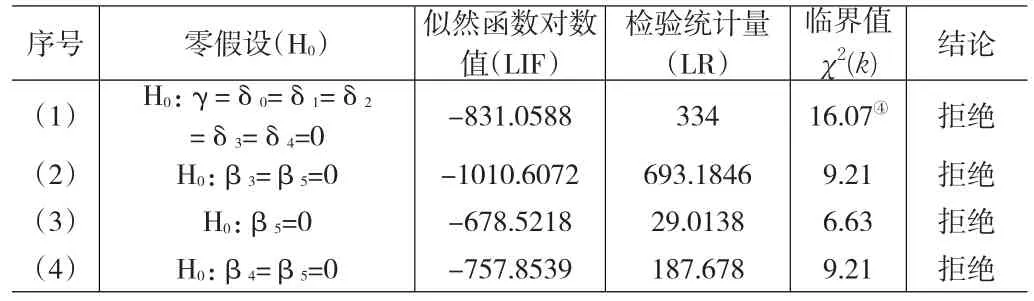
表3 函数的假设检验及结果
根据生产函数(5)和(3)式可知,我国不同地区在各个时期的技术进步率由两部分组成:TPit=0.1875-0.0169lnLit,其中,0.1875表示纯粹的技术变化,代表我国所有地区每年共同的技术进步率为18.75%,这是由技术外溢和扩散效应导致的生产前沿面的移动;-0.0169lnLit表示非中性的技术进步,代表不同地区通过“干中学”所导致的生产前沿面的移动,这种技术进步因地区不同而不同。在此基础上,结合已经得到的技术效率变化率⑤技术效率可由Frontier Version 4.1计算得出,个体i从t到t+1期的技术效率变化率为:TECit,t+1=TEit+1/TEit.,最终可以计算出我国各地区在各个时期的农业全要素生产率的变化率⑥为节省文章篇幅,这里没有列出我国30个地区1980—2009年农业TFP变化率,需要者可与作者联系.。
2 中国农业全要素生产率的收敛分析
2.1 研究方法
从以上的计算结果可以看出,我国地区间农业TFP的变化存在很大的差异。农业TFP的变化是否有利于地区间农业发展差距的缩小,即是否出现了新古典经济理论所认为的经济增长收敛现象是本文将要研究的一个问题。
所谓经济的收敛性是指在投入要素边际产出递减的规律下,经济发展水平较低地区的经济增长速度高于经济发展水平较高的地区,即落后地区具有较高的增长率,最终导致差异逐渐消失的过程。一般将经济增长的收敛性分为四种:σ收敛、绝对β收敛、条件β收敛和俱乐部收敛。σ收敛是指在不同地区之间,人均产出或收入分布的分散程度随着时间的推移而逐渐降低,σ收敛通过观测地区间产出或收入差异来进行验证,通常采用基尼系数、标准差、Theil指数和变异系数进行分析,可以直观的反映地区间的差异是否缩小。β收敛是指期初人均产出较低的个体的人均产出增长率高于期初人均产出较高的个体,体现了落后的经济个体向发达的经济个体的追赶过程。Barro et al(1995)[2]提出的检验β收敛的方程为:

其中,i为地区,t和t+T代表期初和期末,T为时间长度,yi,t和 yi,t+T为地区 i在不同时期的产出,β为收敛速度。如果β>0,则表现为绝对β收敛,地区间的差距将会逐步缩小,意味着不同的地区最终收敛于相同的稳态水平;如果在方程的右边加入其它有关控制变量(如人力资本、基础设施等)之后β>0,则表现为条件β收敛,说明不同地区由于自身条件的差异,最终会收敛于各自的稳态水平。本文根据上一部分采用随机前沿分析得到的农业TFP指数,分析我国不同地区的农业TFP是否存在新古典经济理论认为的收敛趋势。
2.2 收敛的实证检验
在进行σ收敛的实证检验中,不同学者采用不同的指标进行分析,所以得到的结果也存在差异。本文采用运用比较广泛的标准差和变异系数来衡量我国不同地区之间农业TFP指数的σ收敛情况。根据前文得到的计算结果,我国1981~2009年期间农业TFP的标准差和变异系数随时间趋势的变化见图1。

图1 1980~2009年我国农业TFP指数标准差、变异系数的时间趋势图
从图1中可以清楚的看到,我国地区之间农业TFP指数的标准差和变异系数都随着时间的推移而不断增长,直观的说明我国地区之间农业发展水平的差距在不断扩大,我国地区之间的农业发展水平并没有出现收敛趋势。本文采用两个简单的函数形式对这一结论进行进一步验证:,σ为标准差,CV为变异系数,t表示时间变量。从表4中的回归结果看出,,并且参数在1%的水平上具有显著性,所以我国地区间的农业TFP不存在σ收敛。

表4 σ收敛回归分析结果
在进行β收敛的分析中,本文首先采用绝对β收敛检验,根据Barro et a(l1995)[2]提出的方法,本文设定的检验农业TFP收敛的模型的基本形式为:

其中,TFP为地区i在t和t+T时期的全要素生产率指数,,β为收敛速度,T为观测时间长度。在本文中,将样本平均划分为6个时间段,每一时间长度为5年⑦最后一个时间段的长度为4年,这并不会改变估计值的符号。,取2006~2009年各地区农业TFP的平均值作为检验期的TFP,取1981~1985年TFP的平均值作为基期的TFP,两个时间段相隔25年,因此时间长度T取25。对(8)式进行回归分析后所得结果见表5,从表中可以看出,待估参数b的估计值在1%的水平上显著大于0,表明我国地区间的农业TFP并没有出现绝对β收敛,反而具有明显的发散趋势。

表5 绝对β收敛回归分析结果
在进行条件β收敛检验时,本文采用Miller和Upadhyay(2002)[3]提出的面板数据双向固定效应模型进行分析,不需要增加其他的控制变量,避免了人为在选择控制变量时对相关因素的遗漏。该模型能使用最少的数据进行条件β收敛检验,便于展开实证分析。本文采用表达式(9)对我国农业TFP条件β收敛进行分析:
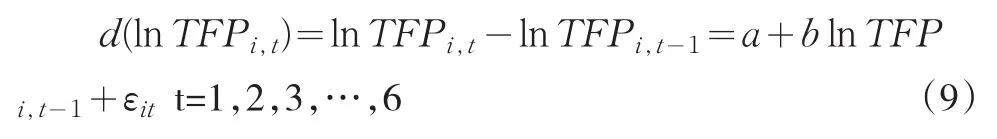
对表达式(9)进行回归分析所得结果见表6,从表中可知,待估参数b虽然小于0,但估计值并不显著,表明我国各地区相对自身而言并没有出现明显的农业TFP收敛趋势。

表6 条件β收敛回归分析结果
3 基本结论
本文利用随机前沿分析方法(SFA)对我国1980~2009年的农业TFP进行测算,从最终的分析结果可以看出,我国农业生产的技术效率总体处于下降趋势,技术效率平均每年以0.88%的速度在下降。全国农业平均的技术效率为61.58%,通过提高化肥施用量、增加播种和有效灌溉面积可以降低农业生产中的技术无效率,提高农业生产效率。我国农业TFP总体处于增长趋势,平均每年以6.87%的速度在增长,但由于技术效率逐年下降,所以农业TFP的增长主要靠农业技术进步的带动,我国农业技术平均每年以7.75%的速度在增长。本文得到的结论与多数学者认为农业TFP的增长主要是由技术进步导致的这一观点相同,所以在农业发展过程中,不能只进行技术的创新和研发,更需要进行适当的制度改革和提高管理水平进而提高技术效率,推动农业TFP更快的增长。
实证分析表明,改革开放后,我国农业发展水平的地区差距不断扩大,农业TFP没有出现σ收敛,同时也没有出现绝对β收敛,而是表现出明显的发散趋势,这说明在不考虑任何因素的条件下,我国地区间的农业全要素生产率随着时间的推移有不断扩大的趋势。本文在考虑随机因素影响后的农业TFP并不存在条件β收敛,也不存在明显的发散趋势或者说只存在很弱的发散趋势,这可能是因为我国农业TFP的增长主要依靠农业技术进步,而农业技术进步又需要高素质人才来推动,高素质人才不同于其它生产要素,其较高的边际收益效应可以弥补资本边际收益的递减效应。我国农业发展水平较高的地区由于具有较多的农业科技人员,所以农业TFP的增长速度较快;反之,落后地区由于缺乏相关科技人员,农业TFP的增长速度相对较慢,最终导致地区间农业TFP的差距不断扩大,所以农业发展较落后的地区应加大对教育的投入,提高农业科技人员所占的比例。这只是本文认为的农业TFP差距不断扩大的原因之一,其它原因还有待进一步分析。
[1]Battese,E,Coelli,T.A Model of Technical Inefficiency Effects in Sto⁃chastic Frontier Production for Panel Date[J].Empirical Economics,1995,(20).
[2]Barro,Robert J.,Xavier,Sala-i-Martin.Economic Growth.New York:McGraw-Hill,1995.
[3]Miller.S,M.Upadhyay.Total Factor Productivity and the Conver⁃gence Hypothesis[J].Journal of Macroeconomics,2002,(24).

