基于混沌特性参数的股指神经网络建模及预测

樊明智，刘道文

（许昌学院a.数学与统计学院；b.公共实验中心，河南 许昌461000）

0 引言

随着我国经济的快速发展，股指预测成了一个当前研究的热点课题，业内专家学者试图通过分析股指的特性，把握其变化规律，从而做出较准确的股票价格指数走势分析。股票市场受多种因素的影响，在较短时期内，股指可能波动较大，表现出明显的非线性和不确定性；但在较长时期内有某些确定的基本因素起作用，股指的变化具有一定的趋势性[1]。在分析股指混沌特性的基础上，寻求一种较理想的股指预测方法具有现实意义。

混沌是指确定性系统中存在的一种貌似无规则、随机的现象，其固有的确定性表明许多貌似随机的现象是可以预测的，一般是将具有混沌特性的时间序列转换到高维空间中，找出蕴涵在混沌吸引子中的演化规律。在实际预测过程中，当嵌入维数较高时，时间序列的相空间轨迹可能很复杂，很难找出一种映射关系来预测未来时刻的数值。而神经网络是通过对简单的非线性函数的多次复合来逼近复杂函数，可以表达复杂的物理现象[2]。从股票市场中提取出来的股指时间序列随时间波动比较剧烈，依据混沌理论计算出来的相空间重构最佳嵌入维数较大。本文将依据混沌理论确定其时间延迟和最佳嵌入维数后，以最佳嵌入维数作为输入结点数目建立神经网络模型来预测股指的未来值。

1 时间序列的相空间重构

股票市场是一个复杂的非线性动力系统，在实际数据分析时往往只是从股票价格随时间变化的时间序列入手。而影响股票市场的因素众多，仅仅依赖时间这一因素来预测股票市场的变化显然存在较大的局限性，利用相空间重构[3]的方法可以将时间序列从一维转换到高维空间中，从而在高维空间中把握系统变化规律，在此基础上进行股票价格指数的预测在理论上是可行的。Takens[4]证明了可以找到一个合适的嵌入维，即如果延迟坐标的维数m≥2d+1，其中d是动力系统的维数，在这个嵌入维空间里可以把有规律的轨迹(吸引子)恢复出来。也即在重构的Rm空间中的轨线上原动力系统保持微分同胚，从而为混沌时间序列的预测奠定了坚实的理论基础。

设时间序列{xi,i=1…N}是从股票市场提取出来的股指时间序列，若序列具有混沌特性，则依据混沌理论计算出该时间序列的延迟时间τ和最佳嵌入维m，根据这两个参数对股指时间序列进行相空间重构，将其从一维转换到高维空间中。相空间重构得到的空间向量为：

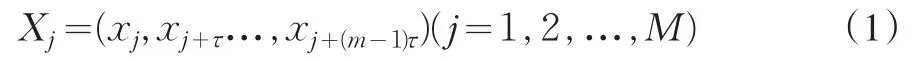
X1,X2,…Xj,…,XM为相空间中的相点，由这些相点构造相空间[X1,X2,…,XM]T。因此，可用这些相点在m维相空间中描述系统的演化轨迹，即有：

状态方程组（2）中的各个方程是关于向量的表达式，为直观地展现历史数据的演化规律，将（2）式表示为关于时间序列数据元素的方程式[5]：

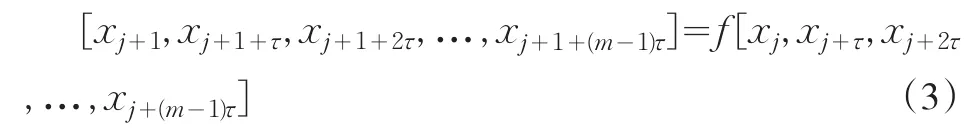
状态空间中相点Xj→Xj+1的演化反映了系统的演化规律，这样可由历史数据预测系统演化趋势[6]。由于相点Xj+1中前（m-1）维是已知的历史数据，将其化为单输出得：

这里F(x)是一个从Rm到R的映射，一般为非线性映射关系，预测问题的实质就是如何获得关于F(x)的一个最佳逼近[7]。

2 神经网络建模

根据历史数据对系统的未来值进行预测实际上是寻求一个历史数据与未来值间的映射，这个映射关系的准确性决定了预测结果的可靠性。神经网络在理论上能实现非线性函数的无限逼近，具有良好的预测能力，因此利用神经网络模型能准确地进行非线性时间序列的预测。根据股指时间序列的特点，本文建立径向基函数（RBF）神经网络预测模型。

RBF神经网络是局部逼近网络，收敛速度快且不易陷入局部最小点，可以在任意精度下逼近任意的非线性函数。本文建立三层网络结构的预测模型（如图1），输入层将变量传输到隐含层，隐含层的基函数采用高斯函数，对输入变量产生局部的响应，隐含层到输出层是一个线性加权的过程。径向基函数为：

式中，Xk是第k个样本向量，Ci是第i个隐含层神经元的中心，δ为宽度值。因此RBF神经网络的输出为：

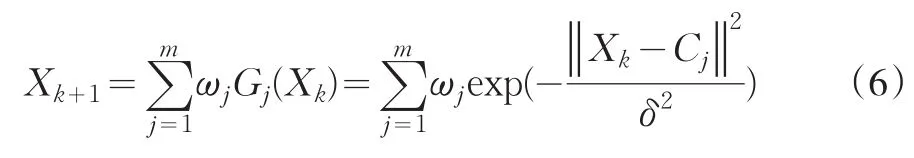
式中，ωj是输出层的连接权值且，Gj(Xk)是第k个样本经过第i个神经元加工得到的输出值。

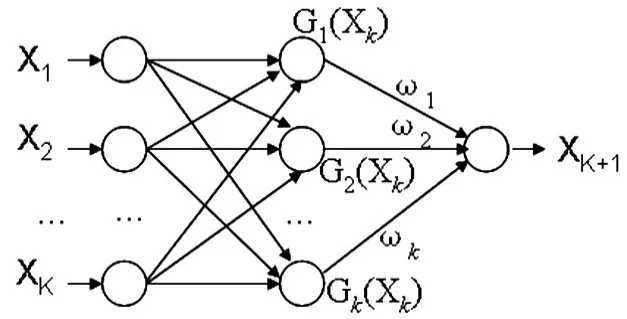
图1 RBF神经网络模型示意图

在RBF神经网络的应用中，神经网络模型每层神经元数目的选取对预测结果的影响具有关键意义。对于混沌时间序列的预测，一般地将该序列相空间重构的最佳嵌入维数作为输入层结点数。研究表明，以此数目作为输入层结点数建立的预测模型具有较好的预测效果[8]。对于隐含层神经元数目的确定本文采取动态调整的方法，事先设定一个精度值，隐含层的神经元数目由小到大增加，当网络预测精度达到设定值时的数目即为隐含层神经元的个数。RBF神经网络的训练分为两步骤：首先确定隐含层径向基函数的中心点，本文采用K-均值聚类算法确定中心点Ci；其次通过最小二乘法修改连接权值。

3 实例分析

3.1 股指序列的提取与处理

在建立神经网络预测模型时，将股指时间序列的最佳嵌入维数作为输入结点的数目，而最佳嵌入维数是依据混沌理论计算得来的。由于依据混沌理论计算延迟时间、嵌入维数等参数时对时间序列的元素数量要求较大，因此选取了上海证券交易所2002年12月11日～2011年3月10日2000个交易日的股指收盘价作为分析对象。为便于混沌特性的分析和计算，将由这2000个数据构成时间序列进行归一化处理。设样本原始数据为{yi,i=1…N,N=2000}，经归一化处理得到的时间序列为{xi,i=1,2…N,N=2000}。

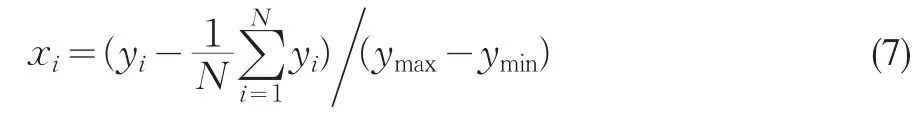
其中，ymax=max{yi,i=1,2…2000};ymin=min{yi,i=1,2… 2000}。

3.2 时间序列混沌特性判定

相空间重构是基于混沌理论的方法，需要证实所研究的对象是一个混沌动力系统或混沌时间序列，因此分析确定股票价格指数时间序列具有混沌特性，是基于混沌理论股票价格指数预测的前提。从股票市场这一非线性动力系统中提取出来的股票价格指数时间序列，其混沌特性可以用该序列的关联维数及最大Lyapunov指数来判定。

关联维是判定一个时间序列具有混沌特性的一个重要特征量，混沌时间序列的关联维数为非整数并且会随着嵌入维数的增大而趋于收敛。确定时间序列的关联维数和嵌入维数最常用方法是G-P法[9]，用此法计算关联维时，需事先计算出时间序列的延迟时间。股指时间序列的数据量很大且具有明显的非线性，本文采用C-C Method[10]法计算其延迟时间τ=24，该方法既能有效地减小互信息法的计算量，又能保持非线性特征。为了直观地观察和分析股指时间序列的混沌特性，在计算其关联维数的同时分别绘制了ln(C(ε))-lnε曲线（如图2）和D(m)-m曲线（如图3）。从图3中可以看出，该时间序列的关联维数随着嵌入维数的增加而趋于收敛，当嵌入维数m等于12时关联维数的值是1.0186，为非整数。

对于离散的非线性时间序列，判定其是否具有混沌特性的另一重要特征量是最大Lyapunov指数。若最大Lyapunov指数λ1＜0，该序列呈现定常或周期状态；λ1＞0意味着该序列具有混沌特性。根据延迟时间τ=24和最佳嵌入维数mmin=12，采用小数据量方法计算出上证指数时间序列的最大Lyapunov指数λ1=0.0033。综上所述，可以判定该时间序列具备混沌特性。

图2 ln(C(ε))-lnε曲线

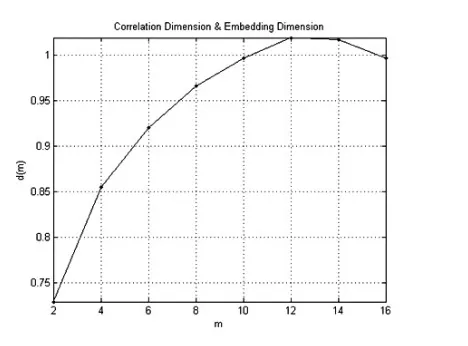
图3 D(m)-m曲线

3.3 数值预测与分析

利用RBF神经网络预测股指时，选用序列{xi,i=1…N,N=2000}的前1600个数据作为训练样本训练神经网络，第1601～2000个数据进行RBF神经网络检验，对股指时间序列最后135个数据进行预测。预测的结果如图4所示。

图4 上证指数源数据与预测值

本文参考文献[6]的评价方法，以预测结果的相对误差评价预测的效果：

4 结论

针对嵌入维数较高的混沌时间序列很难在相空间中找出一种映射关系来预测其变化趋势。本文基于混沌理论计算了上证指数时间序列的混沌特性参数，在相空间基础上建立RBF神经网络预测模型并对上海证券交易所股指时间序列进行了预测。研究结果表明，基于混沌特性参数的神经网络能准确地反映股指变化的趋势，具有较理想的预测效果和应用价值。但该方法仍还有一些值得改进的地方。一方面该方法对历史数据要求严格且计算量大，如何改进算法减小计算量值得进一步研究；另一方面神经网络模型中心点和权值的选择方法有待于进一步优化改进。

[1]鲍新中，刘澄，孙彬.LM-BP算法在金融股指预测中的参数设定[J].系统管理学报，2009,(6).

[2]雷绍兰.基于电力负荷时间序列混沌特性的短期负荷预测方法研究[D].重庆：重庆大学，2005.

[3]吕金虎，张锁春.加权一阶局域法电力系统短期负荷预测中的应用[J].控制理论与应用，2002,（5）.

[4]F.Takens.Determing Strange Attractorsin Turbulence[C].Lecture Notes in Math,898,1981.

[5]乐晓波，匡迎春，唐贤瑛.短期电力负荷的混沌预测及其神经网络的实现[J].长沙理工大学学报（自然科学版），2005,（2）.

[6]张玉梅，曲仕茹，温凯歌.基于混沌和RBF神经网络的短时交通流量预测[J].系统工程，2007,（11）.

[7]侯建军，东防，蔡烽.混沌理论和神经网络相结合的舰船摇荡运动极短期预报[J].舰船科学技术，2008,（1）.

[8]吕金虎，陆安君，陈士华.混沌时间序列分析及其应用[M].武汉：武汉大学出版社，2005.

[9]P.Grassberger，I.Procaccia.Measuring the Strangeness of Strange At⁃tractors[J].Physica D,1983,(9).

[10]H.S.Kim,R.Eykholt,J.D.Salas.Nonlinear Dynamics,Delay Times,and Embedding Windows[J].Physica D,1999,(127).