基于条件风险价值(CVaR)的油气勘探投资组合决策模型研究

王 众，张哨楠,，匡建超，庞河清

(1.成都理工大学能源学院，四川 成都 610059； 2.西南西石油大学资源与环境学院，四川 成都 610500； 3.成都理工大学管理科学学院，四川 成都 610059)

油气勘探属于典型的“三高一长”(高投入，高风险，高收益，长周期)项目，作为石油公司的一项主要投资活动，如何从收益—风险的角度配置好有限资源，降低勘探风险，已成为石油公司面临的艰巨任务[1]。为提高决策质量，理论界和石油公司也在不断探索新的理论及方法，如：模拟仿真、多属性效用决策、现代投资组合理论、实物期权等[2]。其中，尽管现代投资组合理论直到20世纪80年代才在石油工业中得到应用，但近年来随着石油公司海外勘探机会日渐增多、勘探风险日趋增大，现代投资组合理论因其能有效分散投资风险，在一定程度上实现整体勘探投资收益—风险的均衡，受到越来越收多的关注与重视[3]。

目前，国外学者在油气勘探投资组合领域进行了大量研究，如：Davidson(1995)[4]、Orman(1999)[5]、Fichter(2000)[6]、Erdogan(2001)[7]、Garcia(2003)[8]、Walls(2004)[2]等。尽管国内学者从20世纪末21世纪初才开始逐步开展该领域的研究，但仍取得了一定的研究成果，其中具有代表性的有：李玉蓉(2004)[9]、马士忠(2006)[10]、郭秋麟(2007)[11]、王震(2008)[12]、殷爱贞(2010)[13]等。然而通过文献回顾，笔者发现几乎该领域所有的研究都是以Markowitz的均值—方差模型[14-15]为基础，即运用收益的方差(或标准差)来度量勘探投资组合的风险。考虑到金融资产和油气勘探项目的区别，笔者认为运用方差度量风险存在以下缺陷：首先，勘探项目的收益不一定服从正态分布，甚至还存在“高峰、肥尾”现象，方差很难捕捉潜在损失；其次，方差表示的是实际收益偏离平均收益的波动情况，不论高于还是低于平均收益，只要波动越大就认为风险越大，这明显有悖于投资者对风险的真实心理感受；另外，方差只能表示收益波动的幅度，无法明确指出损失的大小。

20世纪90年代，风险价值(VaR)被提出用于代替方差来度量投资组合的风险，但其在使用过程中仍然存在不符合一致性风险度量方法要求、无法考虑尾部风险等缺陷[16]。随着研究的进一步深入，学者又提出了VaR的修正方法——条件风险价值(CVaR)[16-17]。由于CVaR不仅具有VaR的优点，还具有次可加性、凸性等性质，并且可以通过线性规划方法进行求解，则与均值—方差模型类似，CVaR也可用投资组合优化[18]。基于此，本文引入CVaR理论，构建了基于CVaR的勘探投组合决策模型。该模型运用CVaR度量勘探投资组合的风险，通过线性规划求得各项目的最优投资比例，有效克服了方差在勘探项目风险度量上的缺陷，有助于决策者更好地了解勘探投资组合的潜在风险，使得投资决策过程更加科学，结果更加合理。

1 CVaR方法基本原理

设f(x,y):Rn×Rm→R表示一个投资组合的损失函数，x∈X为决策向量(X为投资组合x的可行集)；y∈Rm为随机变量(如收益率等)，假定y的联合概率密度为p(y)且连续，则当y的分布已知时，损失函数f(x,y)为依赖X的随机变量，它不超过某一持有水平α的概率为：

(1)

假设置信水平为β(0≤β≤1)，则投资组合的VaR可表示为：

VaR=αβ(x)=min{α|ψ(x,α)≥β}

(2)

那么根据CVaR的定义——超过VaR损失的期望值，则投资组合的CVaR可以表示为：

CVaR=φβ(x)=E[f(x,y)≥VaR(x)]

(3)

由式(2)和式(3)可以看出，VaR只表示了单一的分位点，而CVaR则表示了尾部损失的平均值，考虑了大于VaR尾部的全部损失，因此用CVaR对风险进行度量更加充分。

由于CVaR里面包含VaR的函数，很难通过定义来直接计算和优化CVaR，Rockafellar和Uryasev(2000)通过定义辅助函数Fβ(x,α)将VaR和CVaR联系起来[14]：

Fβ(x,α)

(4)

其中：

(5)

根据文献[16]可知最小化CVaR的同时，也使得Fβ(x,α)最小化，即：

(6)

且当(x*,α*)为上述优化问题的最优解时，Fβ(x*,α*)为最优的CVaR，x*为最优的投资组合，而a*为相应的VaR。

由于通常情况难以通过解析法求得概率密度p(y)，在实际操作过程中一般运用情景模拟法来进行计算：假设随机变量y在未来有m种变动情况，令每种情况下y的取值为yk(k=1,2,……,m)，则式(4)可用下式近似代替：

(7)

2 基于CVaR的勘探投资组合决策模型

2.1 模型假设

由于勘探项目(圈闭)属于实物资产，同股票、债券等金融资产还存在一定区别，为了将CVaR理论更好的应用于油气勘探的投资决策，同时使分析更具针对性，笔者对模型设定以下5个假设[2,12,19]：

1)假设所有备选项目都已经通过了技术经济评价，认为其经济上合理、技术上可行；且各项目的投资损益能够根据历史数据和模拟仿真得出。

2)假设石油企业的勘探开发资金均为自有资金，不考虑资金的筹集和融资成本。

3)假设一旦发现具有经济价值的油气圈闭，立即进行开发，忽略各种因素对项目开发造成的延缓；同时一旦进入开发阶段，便会持续带来收益(正的现金流)。

4)假设石油公司可以任意选择各项目的投资比例，即各项目的投资比例可为0到100%中的任意数值。然而由于实际情况限制或合同规定，石油公司不能任意改变某一项目的投资额度。本文提出的决策模型仅仅是为了对勘探投资提供一种指导，改善投资组合。

5) 假设石油公司的决策者都是理性经济人，即他们都是在投资风险一定的情况下追求利润最大化，或者在利润一定的情况下追求风险最小化。

2.2 模型构建

设有n个备选勘探项目，各勘探项目在总预算中所占的投资比例为xi(i=1,2,…,n)，则决策变量x=(x1,x2,…,xn)T；设勘探项目i的收益为yi，考虑到油气勘探项目的高投入、高收益特性，为了更直观的反映各项目的损益，本文运用投资回报率(Return of Investment, ROI)来表示yi，则随机变量y=(ROI1,ROI2,…,ROIyn)。因为损失可以用负的收益来表示，则该勘探投资组合的损失函数可以表示为：

f(x,ROI)=-(x1ROI1+x2ROI2+…+xnROIn)=-xTROI

(8)

根据文献[20]，油气勘探项目的ROI可以通过式(9)求出：

(9)

式中：Po为原油价格(美元/桶)；CP为单位开采成本(美元/桶)；B0为原始地质储量(桶)；Rf为地质成功率(%)；Re为采收率(%)；e为美元对人民币汇率；T为税费比例(%)；i为贴现率(%)；I为勘探开发投资(元)；n为项目开采年限(年)。

2.2.1 目标函数的建立

对于投资组合优化模型而言，可以在风险水平一定的条件下使收益最大化，也可以在收益水平一定的条件下使风险最小化。考虑到油气勘探项目的高风险特性，本文将一定收益水平下的CVaR最小化作为投资组合模型的目标函数。将式(10)带入式(9)，则勘探项目投资组合的CVaR可以表示为：

(10)

式中：m是所取历史数据或模拟样本的个数，ROIk表示各个勘探项目的第k(k=1,2,…,m)个历史(或模拟)投资收益率：

(11)

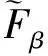
(12)

则该投资组合模型的目标函数为：

(13)

2.2.2 约束条件的建立

由于目标函数推导过程中引入了中间变量Zk，则组合优化模型的第一个约束条件为：

zk≥-xTROIk-α≥0

(14)

风险最小化是基于一定收益水平条件下的，则第二个约束条件为预期收益约束：

(15)

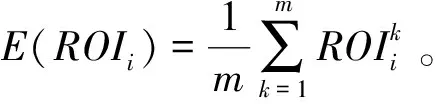
同其他投资项目相比，油气勘探项目除了对投资收益有要求，对提交的储量也有一定要求，则第三个约束条件为数量约束：

(16)

式中：Bi为勘探项目i的地质储量；B0为勘探组合的最低提交储量。

此外，石油公司的资源也是有限的，则第四个约束条件为资本约束：

(17)

式中：Ii为勘探项目i的勘探开发总投资；C0为勘探组合的最大预算资本。

综上，根据式(13)～(17)，油气勘探的投资组合决策模型可以表示为：

(18)

3 算例分析

为了检验模型的实际应用效果，笔者以文献[9]的数据为基础，挑选了5个勘探项目(表1)，运用CVaR投资组合模型对其投资决策进行分析。计算结果科学、合理，符合客观实际。

表1 勘探备选项目基本数据

3.1 ROI模拟

油气勘探是一个复杂的系统工程，涉及的风险因素多而复杂，因此勘探项目的ROI也具有较高的不确定性[21]。本文运用Monte Carlo模拟来计算各勘探项目的ROIk，为简化计算，笔者仅将油价、采收率和单位开采成本作为随机变量，分别反映项目的经济及政治风险、技术风险和财务风险；而根据文献[9]，地质风险通过地质成功率来反映。

假设各项目开采时间均为10年(n=10)，油价服从三角分布(考虑到未来油价难以准确预测，笔者运用2001～2010年10年间的油价来代替，分布参数见图1)，采收率和单位开采成本服从随机分布(分布区间见表1)，美元对人民币汇率为1∶6.5，贴现率i=15%。则根据式(9)，经过200次(m=200)模拟得出各项目的ROIk(图2)。为了更直观的反映各项目的基本情况，笔者对表1和图2的信息进行了进一步整理，见表2。

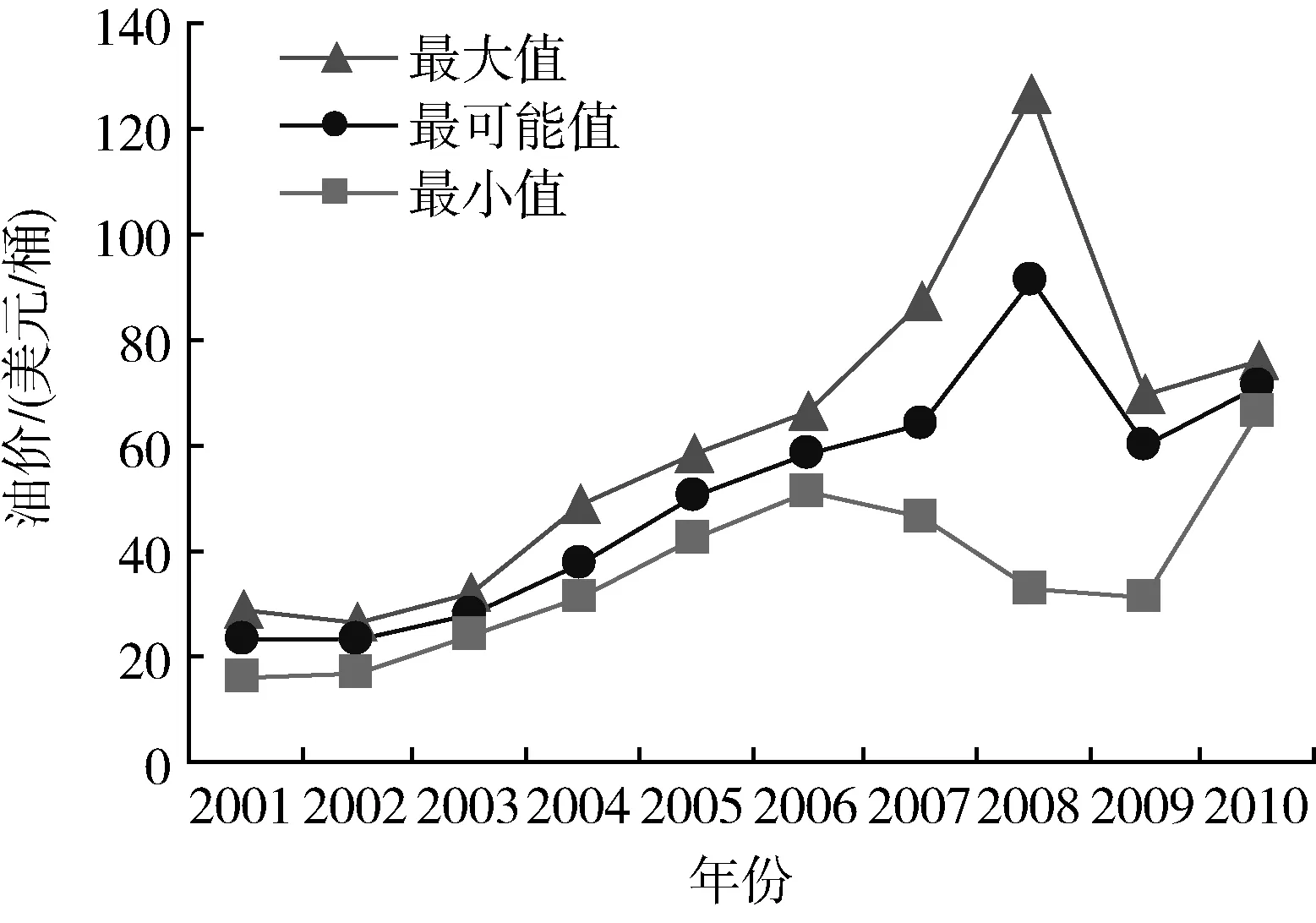
图1 2001～2010年油价变动图

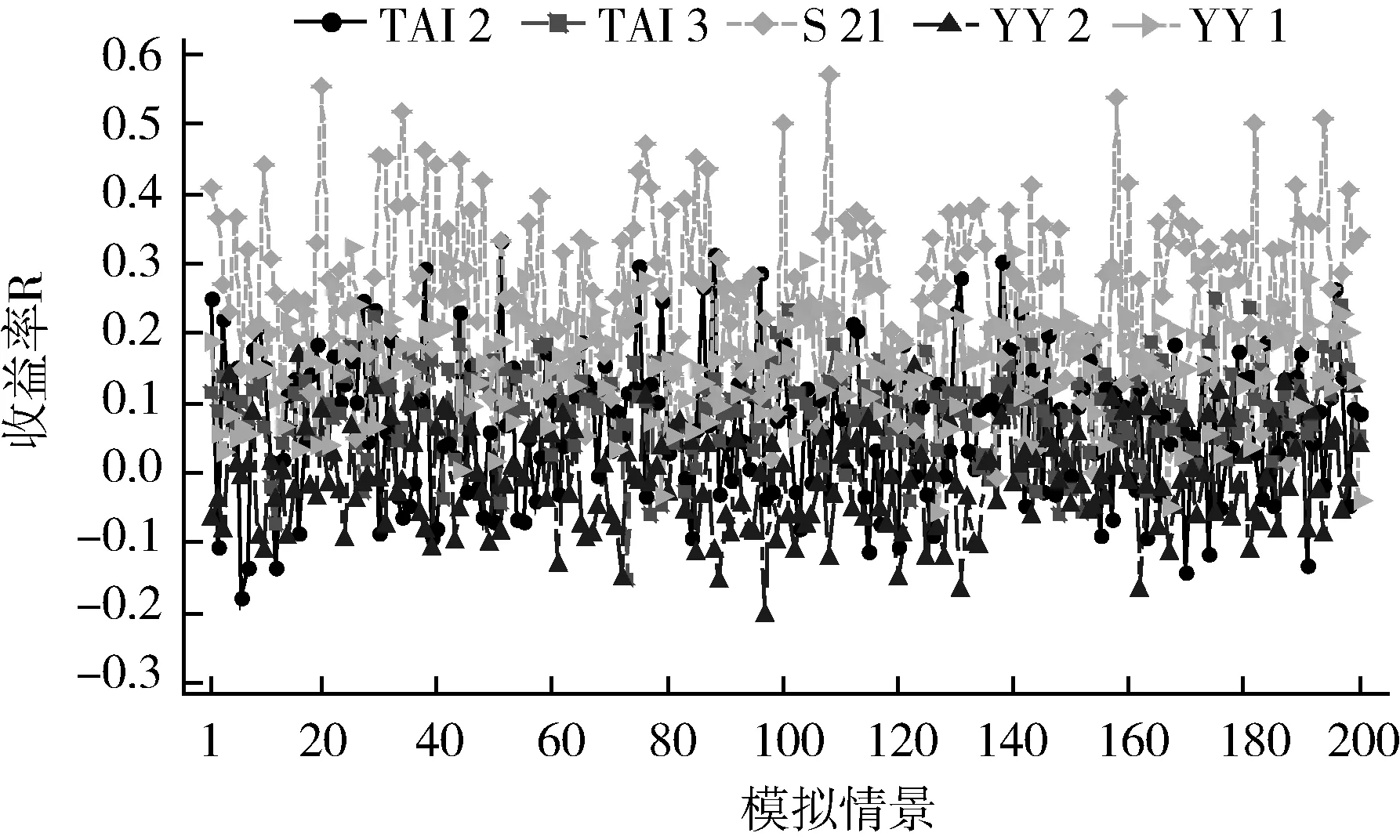
图2 各勘探项目的ROI模拟值

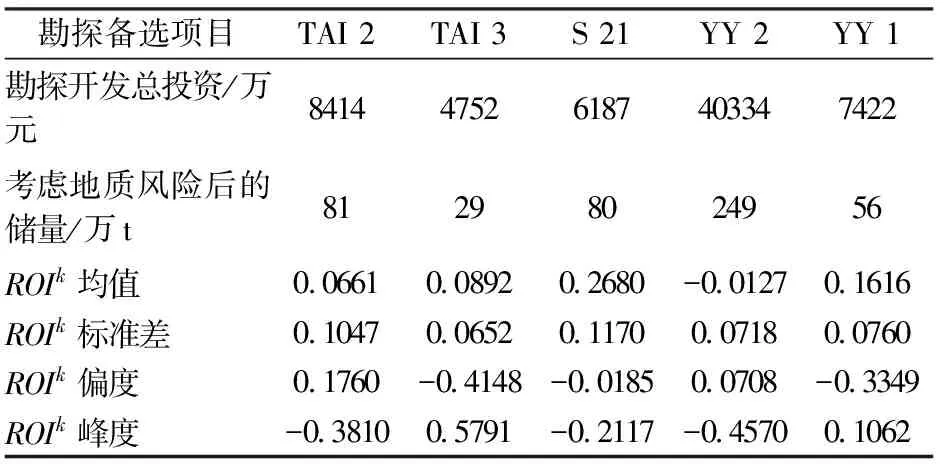
表2 勘探备选项目统计数据

3.2 模型求解

假定石油公司要求最低期望收益率不低于0.21，提交储量不少于85万t，勘探开发总预算9000万元，置信水平β=0.95。根据式(18)，笔者通过Matlab编程计算得到上述约束条件下的最优投资组合x*=(0 0 0.6320 0.0717 0.2963)T，即总预算的63.20%分配给S21，总预算的7.17%分配给YY2，总预算的29.63%分配给YY1。该投资组合相应的VaR和CVaR分别为-0.0905和-0.0657，由于损失是负的收益，则按上述投资比例，在95%的置信水平下，占总投资9.05%的收益不会有损失风险，而超过最小收益的平均收益为投资总额的6.57%。

3.3 模型分析与比较

为了对CVaR投资组合模型有更深入的了解，笔者对模型进行了进一步的探讨和分析。

3.3.1 预期收益和置信水平对投资组合的影响

首先固定β=0.95，观察R0变动对投资组合的影响；然后固定R0=0.15，观察β变动对投资组合变化的影响(表3)。从表3我们可以发现：①同一置信水平下，投资组合的VaR和CVaR随着预期收益的增加而增加，表明收益越高风险越大；②同一收益水平下，投资组合的VaR和CVaR随置信水平的上升而增加，表明随着β值的增大，风险发生的可能性减小，但一旦发生损失将很严重；③同一投资组合，CVaR总是大于VaR，表明在风险度量上CVaR方法更趋保守，更能体现超过VaR的潜在损失；④不论是预期收益还是置信水平的变动都会引起项目投资比例的变化，表明收益水平和置信水平的选取对投资决策有很大影响。

表3 不同预期收益率和不同置信水平条件下的组合优化结果

为了更直观的反映R0和β对投资组合CVaR的影响，笔者分别作出了β=0.90、β=0.95、β=0.99三个置信水平下的CVaR有效前沿(图3)。从图中可以看到同一置信水平条件下，CVaR随着收益的增加而增加；随着置信水平的增大，同一预期收益下的CVaR值也不断增大，相应的有效前沿也随之右移。

3.3.2 约束条件对投资组合的影响

笔者在式(18)的基础上逐渐放宽约束条件，即比较了在β=0.95条件下，不同约束条件下投组合的变动情况(表4)。从表4中可以发现，在仅有预期收益约束(R0≥2.1)的条件下，组合优化模型将投资分配给了期望收益率最大的三个项目，且项目的期望收益率越大，分配投资比例越大；随着储量约束条件(B0≥85)的加入，为满足储量约束，尽管YY2的期望收益最低，还是增大了其投资比例；随着资金约束条件(C0≤9000)的加入，由于YY2和YY1的勘探投资较大，它们的投资比例都有所下降，但由于YY2承担了满足储量约束的任务，其投资比例下降幅度(7.8%)小于YY1的投资比例下降幅度(12.8%)。此外，随着约束条件的不断增加，S21的投资比例逐渐增加，而其余项目的投资比例逐渐降低，CVaR值也不断增加。表明约束条件越多，风险就越不容易分散，投资组合的风险也就越高。

为更直观的反映约束条件对投资组合CVaR的影响，笔者分别作出了不同约束条件下(β=0.95)的CVaR有效前沿(图4)。从图中我们可以看到，随着约束条件的增加，同一R0所对应的CVaR值也逐渐增大，有效前沿也随之右移。在图中，有两个约束条件的CVaR有效前沿同有三个约束条件的CVaR有效前沿部分重叠，表明当R0≥2.16时，新增加的约束条件未起到约束作用。

3.3.3 CVaR投资组合模型与均值-方差模型的比较

为进一步体现CVaR投资组合模型的优点，笔者将该模型同传统的均值—方差模型进行了比较。首先根据文献[12]，在同等约束条件下(R0≥2.1、B0≥85、C0≤9000)构建均值-方差模型，并作出其有效前沿(图5)。

文献[22]指出当指标的偏度(Skewness)绝对值(2、峰度(Kurtosis)绝对值(5时，可认为该组数据基本上服从正态分布)。则根据表2可认为本例中各项目的ROIk基本服从正态分布，那么投资组合的CVaR可以用下式计算[23]：

(19)

式中：Φ(·)为标准正态分布；φ(·)为标准正态分布的密度函数；σP和RP分别为投资组合的标准差和收益率(图5)。则根据图2和式(19)，笔者比较了两个模型各自得出的最优投资比例及相应的CVaR值(表5)。从表5中我们可以发现，当R0=0.15时，均值-方差模型和CVaR模型的结果差别较大，前者将资金分配给了标准差较小的项目，而后者则是将在资金分配给了收益较大的项目；当R0=0.22时，两者求出的投资组合差别较小。但在以上两个收益条件下，CVaR模型求出的CVaR更小，表明CVaR模型求出的投资组合风险更小。

为了更清楚的比较，笔者分别作出了两个模型放在均值-CVaR系统中，作出了两者的有效前沿(图6)。从图6中我们可以看出：在收益相同的情况下，采用CVaR模型求出的最优组合的 CVaR 比其均值-方差模型求得的CVaR要小；此外，当R0≤2.2时，均值-方差模型的有效前沿同一般理论相悖的(收益越小，风险反而增大)。这充分表明在勘探项目的投资组合决策中，CVaR模型要优于传统的均值-方差模型。

表4 约束条件下的投组合优化结果

表5 均值-方差模型和CVaR投资组合模型的比较

图3 不同置信水平下的CVaR有效前沿

图4 不同约束条件下的CVaR有效前沿

图5 均值-方差模型的有效前沿

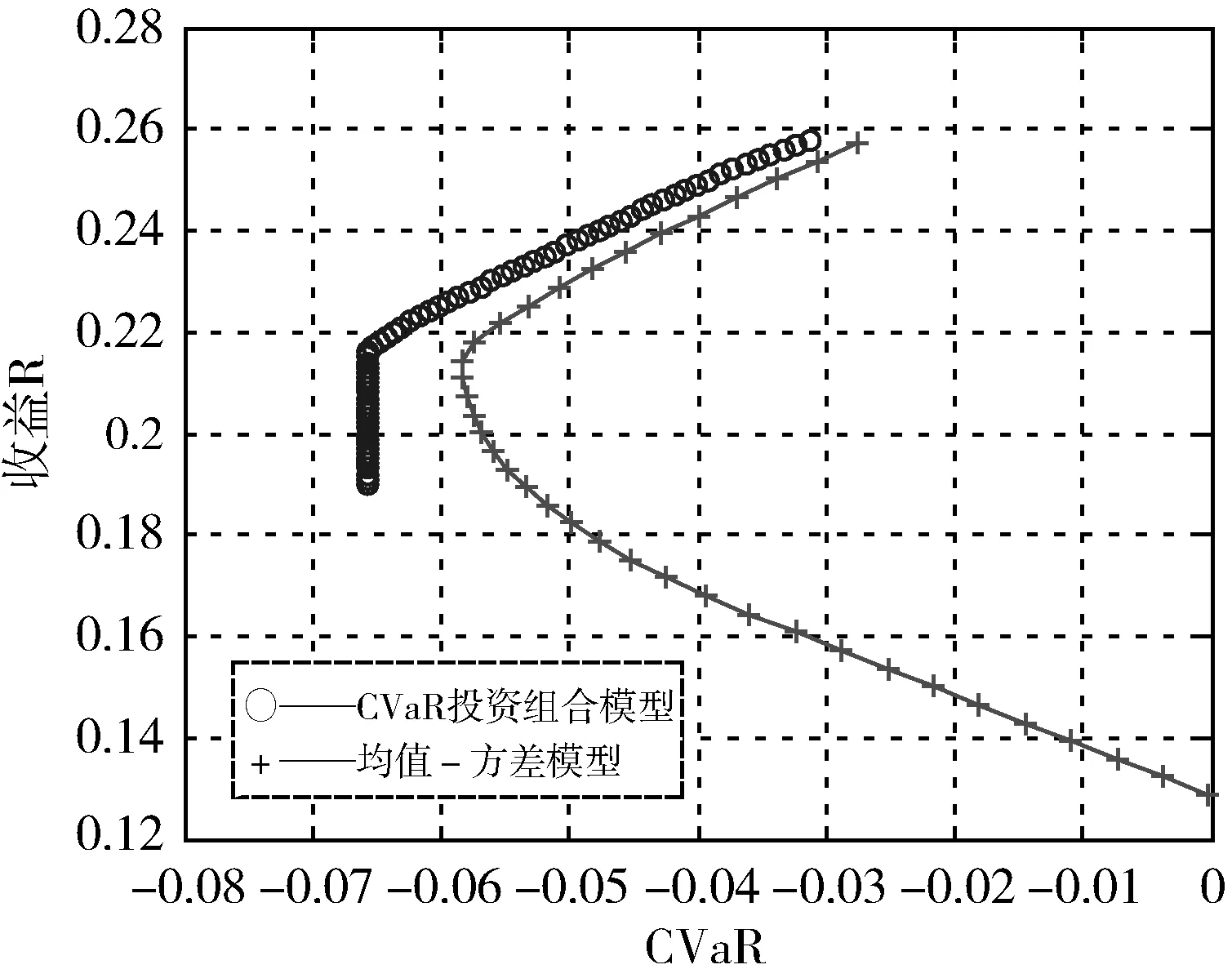
图6 均值-方差模型和CVaR模型的有效前沿对比

4 结语

近年来，着石油公司海外勘探机会日渐增多、勘探风险日趋增大，如何有效分散投资风险，扩大投资效益，从收益-风险的角度做出科学的投资决策已成为石油公司决策层面临的艰巨任务和亟待解决的难题。本文以现代投资组合理论为基础，引入条件风险价值(CVaR)相关理论和方法，构建了基于CVaR的油气勘探投资组合决策模型。该模型运用CVaR度量勘探投资组合的风险，通过线性规划求得各项目的最优投资比例，不仅继承了传统均值-方差模型分散投资风险的优点，同时也有效克服了方差在勘探项目风险度量上的缺陷，有助于决策者更好地了解勘探投资组合的潜在风险，使得投资决策过程更加科学，结果更加合理。

[1] 王众,张哨楠,匡建超. 基于动态MAUT的油气勘探风险决策模型研究[J]. 中国矿业, 2010,19(1):110-113.

[2] M. R. Walls. Combining decision analysis and portfolio management to improve project selection in the exploration and production firm[J]. Journal of Petroleum Science and Engineering, 2004, 44(1-2):55-65.

[3] S. B. Suslick, D. J. Schiozer. Risk analysis applied to petroleum exploration and production: an overview[J]. Journal of Petroleum Science and Engineering, 2004, 44(1-2):1-9.

[4] L. B. Davidson, J. E. Davies. Simple, effective models for evaluating portfolios of exploration and production projects[A]. SPE Annual Technical Conference and Exhibition[C]. Texas, Society of Petroleum Engineers, 1995.

[5] M. M. Orman, T. E. Duggan. Applying modern portfolio theory to upstream investment decision making[J]. Journal of Petroleum Technology, 1999, 51(3):50-53.

[6] D. P. Fichter. Application of genetic algorithms in portfolio optimization for the oil and gas industry[A]. SPE Annual Technical Conference and Exhibition[C]. Texas, Society of Petroleum Engineers, 2000.

[7] M. Erdogan, B. Mudford, G. Chenoweth, et al. Optimization of decision tree and simulation portfolios: A comparison[A]. SPE Hydrocarbon Economics and Evaluation Symposium[C]. Texas, Society of Petroleum Engineers, 2001.

[8] J. Garcia, M. H. Holtz, A. John, et al. Integrated prospect portfolio management for 3D seismic volumes combining geologic, engineering, and economic risk[A]. SPE Hydrocarbon Economics and Evaluation Symposium[C]. Texas, Society of Petroleum Engineers, 2003.

[9] 李玉蓉,李霞,陈光海,等. 遗传算法——国际石油合作勘探开发项目投资组合的新方法[J]. 海洋石油, 2004, 24(2):50-56.

[10] 马士忠,陈昭年,张建宁. 一种油气圈闭组合勘探优化计算方法[J]. 地质论评, 2006, 52(3):423-427.

[11] 郭秋麟. 考虑地质风险的勘探项目投资组合优化模型[J]. 石油勘探与开发, 2007, 34(6): 760-764.

[12] 王震,王恺. 基于Markowitz资产组合理论的油气勘探开发投资决策[J]. 中国石油大学学报：自然科学版, 2008,32(1):152-155.

[13] 殷爱贞,张孟. 基于风险和收益权衡的勘探项目投资组合研究[J]. 西南石油大学学报：社会科学版, 2010,3(1):10-14.

[14] H. Markowitz. Portfolio selection[J]. The Journal of Finance, 1952, 7(1): 77-91.

[15] H. Markowitz. The optimization of a quadratic function subject to linear constraints[J]. Naval Research Logistics Quarterly, 1956, 3(1-2):111-133.

[16] R. T. Rockafellar, S. Uryasev. Optimization of conditional value-at-risk[J]. The Journal of Risk, 2000, 2(3): 21-41.

[17] P. Krokhmal, S. Uryasev. Portfolio optimization with conditional value-at-risk objective and constraints[J]. The Journal of Risk, 2001, 4(2):11-27.

[18] 陈剑利,李胜宏. CVaR风险度量模型在投资组合中的运用[J]. 运筹与管理, 2004, 13(1):95-99.

[19] 王娜. 基于CVaR的房地产投资组合与风险度量研究[D]. 西安：西安科技大学, 2009.

[20] 孙景民,庞雄奇,岳仲金,等. 勘探单项目风险分析技术[J]. 资源与产业, 2008, 7(4): 53-57.

[21] 王众. 天然气勘探风险评价与决策研究——以四川XC气田为例[D]. 成都：成都理工大学, 2009.

[22] 林友威. 房地产投资组合优化及风险度量模型研究[D]. 杭州：浙江大学, 2007.

[23] 陈静. 基于CVaR的投资组合风险管理模型及实证研究[D]. 长沙：中南大学, 2008.