基于期权理论的铁路货运定价模型*

冯芬玲，李菲菲

(中南大学交通运输工程学院，湖南长沙410075)

在铁路货运市场中，铁路运输企业通常提前较长时间(1年或半年)与一些客户(货主或协议客户)签订运输协议，如煤炭、矿石等大型企业。这些客户(以下称为协议客户)采用协议价格，为铁路部门提供稳定的大宗货源，铁路为协议客户提供运力保证。对于剩余的运力，铁路运输企业直接在现货市场中进行销售。由于现货市场价格是不断变化的，使得交易稳定性很差，铁路运输企业不能及时出售运力的风险性就会很高;协议销售能维持平稳的销售情况，但在协议期内，协议客户只能以固定的价格从铁路运输企业购买一定数量的运力，铁路运输企业也只能执行协议价格，双方都不能在市场价格的波动中获利，这对实现自身利益最大化是很不利的。期权是指一种合约，该合约赋予合约持有人在某一特定日期或该日期之前的任何时间以固定价格购进或售出一种资产的权利，该日期过后，期权权利失效，而铁路货物运输在某一时段之后，未出售的产品价值也会归零，可以看出，铁路货运协议销售与期权是十分相似的，它们都是在特定的时期内以特定的价格进行交易，都具有很强的时效性特点，并且期权的价格是随其标的物价格的波动而波动的，其标的物的价格又是由市场波动所决定的，这样就可以有效地规避由于市场价格变动造成的不利影响，因此，将期权理论引入铁路货运市场中具有重要的意义。

目前关于期权契约等各种供应链契约的文献很多，Ritchken［1］等最早在库存研究中引入期权机制以对冲产品价格和数量波动的风险，此后，期权因其弹性被越来越多的学者所青睐而被应用到供应链协调的研究中，例如，Cachon［2］等通过期权契约以实现供应链中的信息共享;Seifert［3］等研究了期权价格为外生变量时具有风险偏好的买方的最优订购决策;郭琼［4－6］等建立了电子市场与传统契约市场共存下的供应链各决策主体的决策模型;赵霞［7］等分析了现货市场和期权合约市场同时存在时零售商的最优购买策略;刘晋［8］等研究了基于期权的供应链模型;佟斌［9］等建立了基于需求预测的两阶段生产和订购模式下的集中决策型和合作型供应链中各决策主体的决策模型;马成［10－11］等也对此进行了相关的研究。

但是将期权契约应用于货运业，特别是铁路货运业的研究还不是很多，尤其是在国内还鲜有文献涉猎。Rol［12］通过建立运力期权定价模型将期权契约应用于航空货运业，赵明瑞［13－14］等对航空货运的期权销售模式进行了初探;雷丽彩［15］等构建了一个基于风险规避的航空货运期权定价模型，这些对研究铁路货运业的期权定价模型有一定的参考作用，但铁路货运业有自己的特点，并不是完全类同于航空货运业，所以，本文拟在前人研究的基础上，根据铁路货运业自身的特性，在铁路货运市场中引入期权的概念，建立铁路货运业的期权定价模型，通过相应的数学推导分析，分别为协议客户和铁路运输企业作出决策建议，以期实现铁路运输企业和协议客户的双赢。

1 铁路货运期权的设计

期权合约按照授予期权持有人权利的类别，可以分为看涨期权和看跌期权。其中看涨期权是指期权赋予持有人在到期日或到期日之前，以固定价格购买标的资产的权利。其赋予权利的特征是“购买”。由于本文中对铁路货运期权的设计是指赋予协议客户以固定价格购买期权的权利，故只会出现看涨期权。

1．1 铁路货运期权的概念

根据上述期权的特性，提出铁路货运期权的概念并对其进行定义。本文中铁路货运期权是指以铁路货物运输服务为标的资产的一种期权合约，铁路运输企业是期权的制定方，协议客户是期权的购买方。如果到期日期权的执行价格高于现货市场货运价格，协议客户会选择执行期权;反之，协议客户就会放弃执行期权而在现货市场中购买运力。这种选择权使得协议客户有效规避了价格波动风险。而对于铁路运输企业来说，在协议客户放弃执行期权时可以在现货市场中进行销售，并且可以收取一定的期权费用，从而可以将部分风险转嫁给协议客户，也有效实现了风险规避。本文假设铁路运输企业和协议客户都是经济人，在进行决策时都会在给定条件下做出自身利益最大化的理性选择。

1．2 铁路货运期权的内容

根据金融市场中期权的概念，结合铁路货运市场的具体特点，铁路货运期权的内容至少应包括以下几点。

(1)标的资产。标的资产是指期权合约中所指定的双方要交易的商品，它可以是某种实物资产或金融资产，也可以是某种服务。铁路货运期权的标的资产就是铁路的货物运输服务。

(2)执行价格。在期权合约中约定的、期权持有人据以购进或售出标的资产的固定价格，称为执行价格。铁路货运期权中执行价格，就是指在货运期权中事先规定的，协议客户在行使其获得相应的铁路运输服务的权利时，需要支付给铁路运输企业的运输服务价格。

(3)数量。铁路运力期权中应明确规定协议客户有权以约定的价格即期权执行价格获得的运输服务的数量即货物运输吨数。

(4)期权到期日。铁路运输企业与协议客户约定的期权到期的那一天称为“到期日”。在那一天之后，期权失效。若协议客户只能在到期日执行期权，则称为欧式期权;若该期权可以在到期日或到期日之前的任何时间执行，则称为美式期权。为了便于研究，本文规定协议客户只能在到期日进行选择，即货运期权为欧式期权，且假定期权的行使期限为1月。

除了上述4项基本内容以外，铁路货运期权还有1个重要的因素就是期权价格，即协议客户支付给铁路运输企业购买期权的费用。

2 基于期权设计的铁路货运定价分析

2．1 问题说明

根据上述铁路货运期权的内容，在引入期权的货运市场中铁路运输企业和协议客户的交易过程如图1所示。

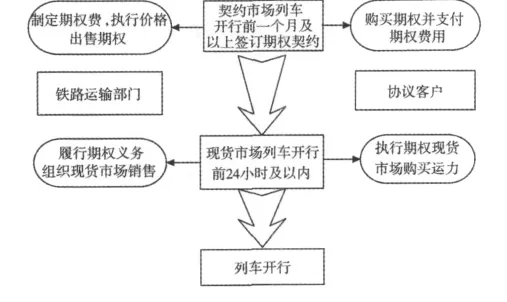
图1 引入期权的货运市场交易过程Fig．1 Trading process in freight market by the introduction of options

通过铁路运力期权的设计，协议客户和铁路运输企业均可以从市场的波动和价格的变化中获利，但是，在铁路运力期权的应用过程中有几个很现实的问题需要解决:

(1)期权费用制定为多少比较合理?若定价太高，协议客户可能会放弃购买期权而宁愿承担现货市场的风险，铁路运输企业也会失去大量的货源;若定价太低，铁路运输企业可能不足以弥补在协议客户执行期权时所遭受的损失。

(2)如何确定期权的执行价格?如果协议客户认为在期权到期日的现货市场价格会和期权执行价格相当甚至低于契约中规定的期权执行价格，那么协议客户肯定不会购买该期权。

(3)对于协议客户来讲，购买运力期权的数量应该是多少合适，是不是越多越好?

因此，在货运市场中引入期权时必须首先解决这3个问题，即期权费用、执行价格的确定以及协议客户的最优期权购买数量。

本文利用动态规划逆向推理的方法，首先根据金融市场中相关知识，利用二叉树模型在对期权执行价格已知的情况下对铁路运输企业销售的期权进行定价，然后基于铁路运输企业和协议客户收益最大化的最优决策模型，解决期权执行价格制定和期权购买数量的问题。

2．2 研究假设

假设1:按照需求曲线，协议客户的市场期望收益为市场需求D的函数，需求量D与现货市场货物的售价p一般是负相关的。因此，假设需求D=a－bp+ε，ε是分布函数为F(x)，密度函数为f(x)的随机分布。

假设2:在t=0时，协议客户不知道t=T时的现货市场运力价格，但是知道现货市场运力价格的分布。本文中假设现货市场运力的价格将是两种可能值中的一种，即上升到一定的百分比，或者下降到一定的百分比。

2．3 符号定义

设s0为t=0时现货市场中单位运力的价格;su为到期日现货市场价格上行时单位运力价格;sd为到期日现货市场价格下行时单位运力价格;u为现货市场单位运力价格上行乘数;d为现货市场单位运力价格下行乘数;r为无风险利率;c0为铁路货运期权单位运力的期权费用;cu为现货市场价格上行时铁路货运期权到期日价值;cd为现货市场价格下行时铁路货运期权到期日价值;c为铁路货运期权的单位运力的期权执行价格;n为协议客户的期权购买量;b0为铁路提供单位运力的长期准备成本;b1为铁路提供单位运力的短期生产成本;K为铁路货物运输的总运输能力;C为单位运力的固定生产成本。

2．4 模型的建立

2．4．1 二叉树期权定价模型的建立

在利用二叉树模型进行定价时需要建立在以下假设基础之上。

假设1:在该模型中期权的执行价格为外生变量，期权费用是受期权执行价格影响的内生变量。

假设2:铁路运输企业和协议客户都是现货市场货运价格的接受者，货运价格受铁路货运市场收益率标准差的影响。

统计并对比护理干预前后两组心理状态的变化情况和疾病健康知识掌握能力。①根据患者焦虑、抑郁评分的变化评测其心理状态,其中得分愈高提示焦虑情绪和抑郁状态愈严重,焦虑总分为100分,抑郁总分为10分;②自拟调查问卷表并回收有效问卷,采用百分制进行得分统计,90分及以上为优,60-89分之间为良,低于60分为差。

假设3:协议客户为风险规避型的，持有期权的期望报酬率为无风险利率。

假设4:铁路货运期权只能在到期日执行，即为欧式期权。

(1)单期二叉树模型。期权的到期日价值受现货市场价格和期权执行价格的影响，若到期日现货市场的货运价格高于期权执行价格，则期权的价值=现货市场货运价格－期权执行价格，若到期日现货市场价格低于期权执行价格，则期权的价值为0，此时协议客户放弃执行期权，用二叉树可以表示为如图2所示。

图2 单期二叉树Fig．2 Single－phase binary tree

协议客户持有期权的期望报酬率=无风险利率=上行概率×价格上升百分比+下行概率×(－价格下降百分比)=上行概率×(上行乘数－1)+下行概率×(下行乘数+1)，即为

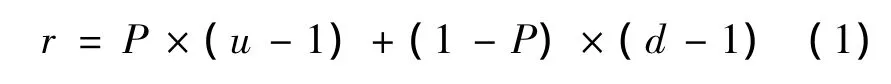
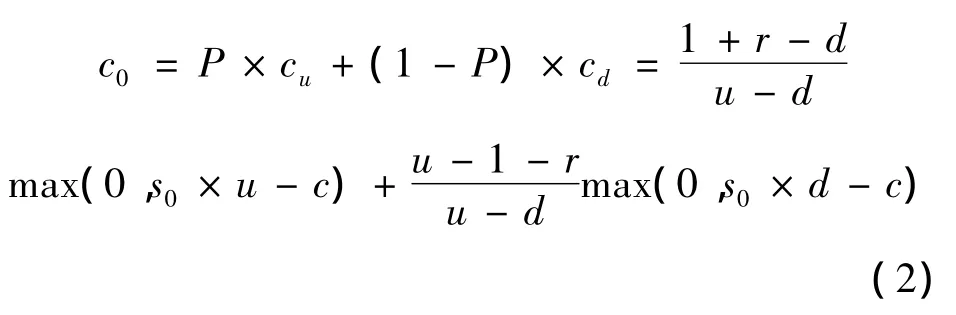
即期权费用c0=c0(c，s0)。

(2)多期二叉树模型。单期的定价模型假设本来现货市场单位运力的价格只有两个可能，对于时间很短的货运期权来说时可以接受的，若到期时间较长，如本文中1月的时间，就与事实相去甚远。改善的办法是把到期时间分割成多部分，就可以使期权价值更接近实际。从原理上看，与两期模型一样，从后向前逐级推进，只不过多了几个层次。期数增加以后带来的主要问题是现货市场单位运力价格上升与下降的百分比确定问题。期数增加以后，要调整价格变化的升降幅度，以保证货运市场年收益率的标准差不变。可以假设年收益率与升降百分比满足以下的等式:

式中:e为自然常数，约等于2．718 3;σ为铁路货运市场收益率的标准差;t为以年表示的时间长度。

设:suu为现货市场中单位运力价格在多个时期都上升;sdd为现货市场中单位运力价格在多个时期都下降;sud为现货市场中单位运力价格在一个时期上升，另一个时期下降;cuu为现货市场单位运力价格都上升的铁路期权价值;cud为现货市场单位运力价格都下降的铁路期权价值;cdd为现货市场单位运力价格一个时期上升一个时期下降的期权价值。用二叉树表示如图3所示。

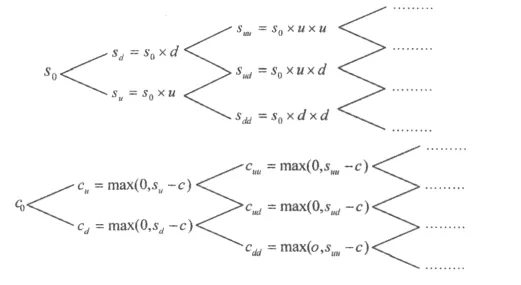
图3 多期二叉树Fig．3 Multi－ period binary tree

c0根据单期二叉树模型从后向前逐级推进。以2期二叉树模型为例:

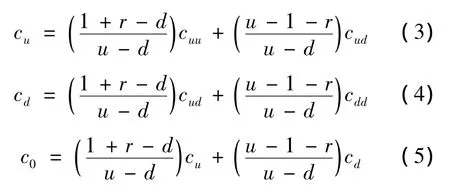
同样地，c0是关于期权执行价格c和现货市场货运价格s0的变量，即可以表示为c0(c，s0)。

2．4．2 执行价格以及期权购买量的确定

(1)问题描述。假设现货市场运力价格为2种价格中的1种，上升为su的概率为P，下降为sd的概率为1－P。

铁路运输企业与协议客户在进行交易时具体操作顺序如下:

①铁路运输企业制定期权费用c0和期权执行价格 c。

②协议客户根据铁路运输企业制定的期权定价政策(c0，c)，根据其对市场的预期收益效用函数，选择最优运力订购量n，并支付期权费用c0n。

③在期权的交易日，协议客户根据现货市场的价格和期权的执行价格来决定是否执行期权以及其在现货市场的运力购买量。

④铁路运输企业支付长期准备成本和短期准备成本，并支付固定生产成本KC。

(2)模型建立。对协议客户的最优期权购买量以及铁路运输企业最优期权执行价格的确定均需要分情况讨论。

情况1:当t=T时，若现货市场的运力价格为低价sd＜c，协议客户选择直接从现货市场购买，放弃使用期权。

协议客户的利润函数为:

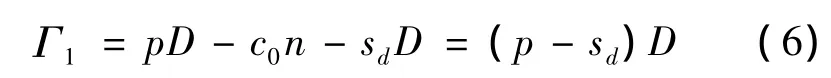
铁路运输企业的利润函数为:

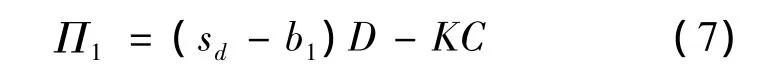
代入D=a－bp+ε，可得协议客户和铁路运输企业利润的期望值分别为:

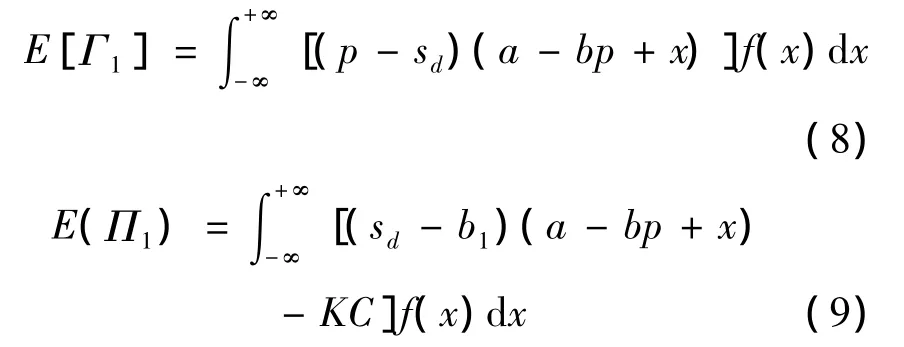
情况2:当t=T时，若现货市场的运价为高价su＞c，协议客户尽量使用期权以减少运力成本。如果t=0时购买的期权数量大于t=T时的实际需求量，则只需要执行期权来满足需求。如果t=0时购买的期权数量小于t=T时的实际需求量，则除了执行期权，还需要从现货市场中购买运力以满足需求。

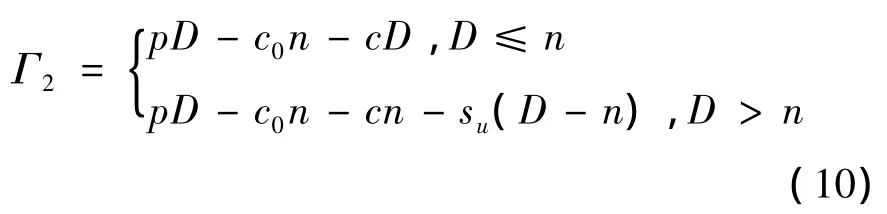
协议客户的利润函数为:铁路运输企业的利润函数为:

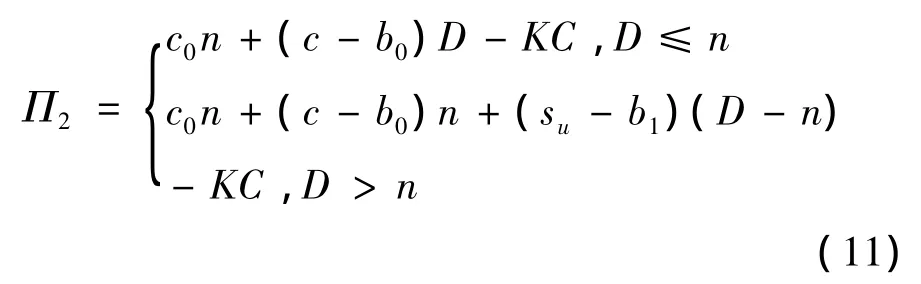
代入D=a－bp+ε，可得协议客户和铁路运输企业的利润的函数分别为:

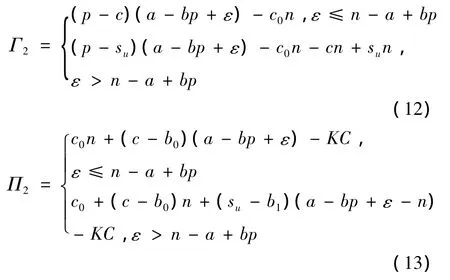
则利润的期望值分别为:

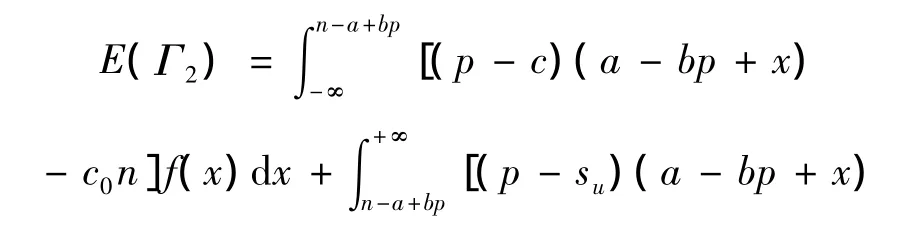
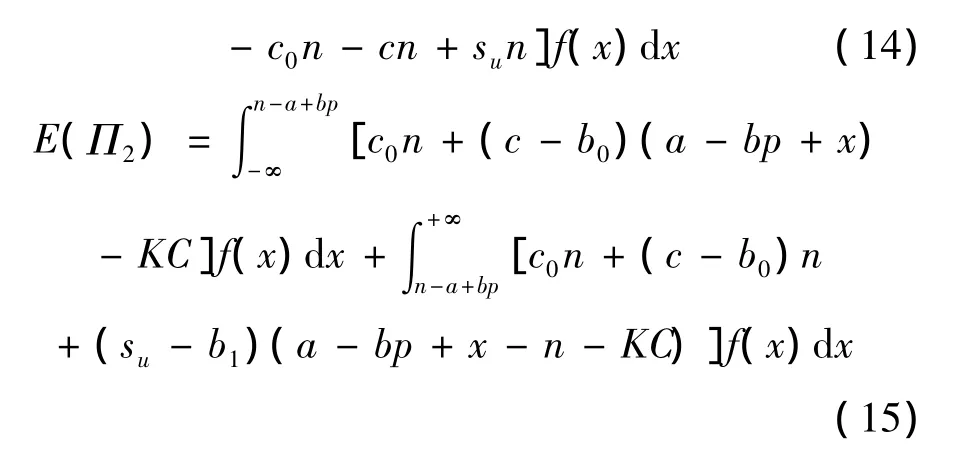
结合情况1和情况2，则协议客户的利润期望值为:

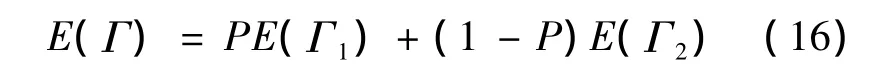
对E(Γ)求n的一阶导数，可得:

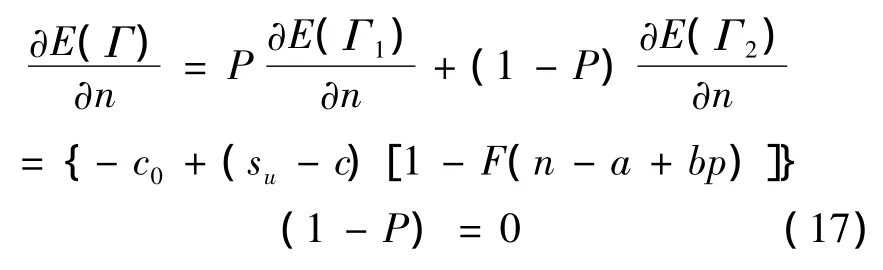
则可得到协议客户的最优期权购买量n满足的条件为:

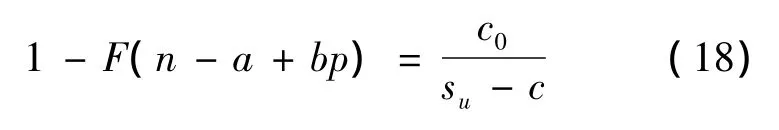
同样，铁路运输企业的利润期望值为:

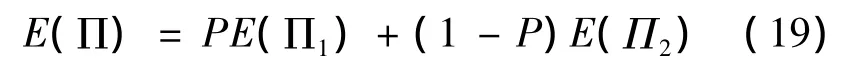
对E(Π)求n的一阶导数，可得:

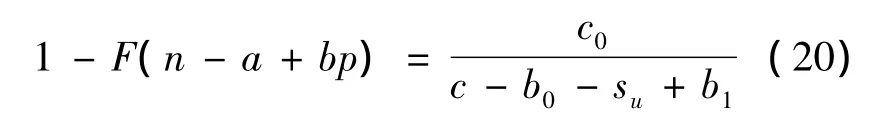
结合式(18)和(20)可得铁路运输企业的最优期权执行价格:

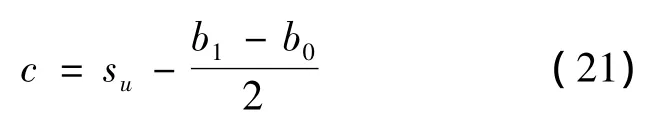
3 算例分析

假设铁路货运市场提前1月制定期权价格与期权费用，协议客户根据其定价政策选择其最优期权订购量，在现货市场中根据现货市场价格决定期权执行量。

假设在期权到期日存在现货市场，且ε的分布为满足［－200，+200］均匀分布，密度函数为:

分布函数为:

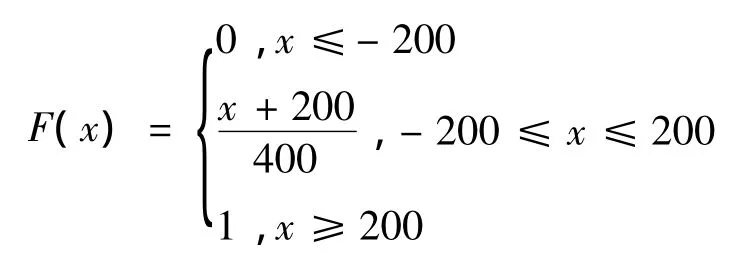
设长期生产成本为b0=160，短期生产成本b1=240，市场无风险利率r=4%，以两期二叉树模型为例，若期权制定前1天现货市场运力价格s0=200，市场收益率标准差σ =0．4068，则上行乘数u=1．1246，下行乘数 d=0．8892，可以计算出上行概率 P=0．64，下行概率1 － P 为0．36，则在单期二叉树树模型中，su=220。

据此，根据式(21)可得最优期权执行价格c=180。可以看出:铁路运输企业制定的协议价格相比现货市场的运力价格下降了18%，其大小与现货市场运力价格、长期准备成本、短期准备成本相关。

为了使求得的期权费用更加精确，采用两期二叉树模型求解期权费用，如图4所示。

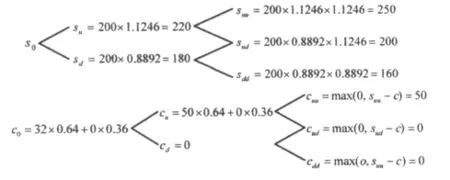
图4 两期二叉树求解过程Fig．1 Two－period binary tree sdution process

可以求得期权的费用c0=20。

总结求解最优期权订购量的相关条件为:

c0=20，c=180，su=220，假定 D=a － bp+ε 中，a=1000，b=0．5，p=500，把上述条件代入公式(18)可得协议客户最优期权订购量为:n=750。

综上所述，可得铁路运输企业的最优定价策略:c=180，c0=20;协议客户的最优期权购买量n=750。

根据上述假定和结论，计算在铁路运输企业制定不同的价格政策时协议客户的最优期权订购量，其结果如表1所示。

表1 最优期权订购量对定价政策的敏感性分析Table 1 Sensitivity analysis of the optimal quantity to pricing policy

从表1可以看出:在期权执行价格给定的情况下，随着期权价格的升高，协议客户的期权购买量逐渐减少;在期权价格给定的情况下，随着期权执行价格的升高，协议客户的期权购买量逐渐减少。这是因为:随着期权成本的上升，期权执行价格的上升，协议客户比较倾向直接在现货市场中购买运力，而不是购买期权。

4 结论

(1)铁路运输企业制定的协议价格与现货市场价格、铁路运输企业的长期准备成本正相关，与铁路运输企业短期准备成本负相关。

(2)协议客户的最优期权购买量与期权价格、期权执行价格负相关。

本文设计的模型仅考虑了铁路运输企业和协议客户之间的供求关系，并没有考虑实际市场中铁路运输企业与其他运输方式之间的竞争。

［1］Ritchken P，Tapiero C．Contingent claims contracting for purchasing decision in inventory management［J］．Operation Research，1986，34(6):864 －870．

［2］Cachon G，Lariviere M．Contracting to assure supply:How to share demand forecasts in a supply chain［J］．Management Science，2001，47(5):629 －646．

［3］Seifert，Ralf W Thonemann，Ulrich W Hausman，et al．Optimal procurement strategies for online spot markets［J］．European J of Operational Research，2004，152(3):781 －799．

［4］郭 琼，杨德礼．基于期权与现货市场的供应链契约式协调的研究［J］．控制与决策，2006，21(11):1229－1234．GUO Qiong，YANG De-li．On supply chain coordination with contract based on option and spot market［J］．Control and Decision，2006，21(11)，1229 －1234．

［5］郭 琼．基于期权契约的供应链协作模型的研究［D］．大连:大连理工大学，2006．GUO Qiong．Research on supply chain coordination with option contracts［D］．Dalian:Dalian University of Technology，2006．

［6］郭 琼，迟国泰．基于期权的供应链契约式协调模型［J］．系统工程，2005，23(10):1 －6．GUO Qiong，CHI Guo-tai．Supply chain cooraination with option contract［J］．Systems Engineering，2005，23(10):1－6．

［7］赵 霞，黄培清．一种基于期权合约和现货市场的零售商采购模型研究［J］．科学技术与工程，2009，9(4):1085－1088．ZHAO Xia，HUANG Pei-qing．Model for retailer’s procurement based on option contract and spot market［J］．Science Technology and Engineering，2009，9(4):1085 －1088．

［8］刘 晋，段 毅．基于期权的供应链伙伴关系管理［J］．统计与决策，2008(14):62－64．LIU Jin，DUAN Yi．Supply chain partnership management based on the options［J］．Statistics and Decision，2008(14):62－64．

［9］佟 斌，潘 新．基于需求预测的供应链期权式契约协调［J］．系统工程，2006，24(11):13 －18．TONG Bin，PAN Xin．Supply chain coordination with option contract under demand updating［J］．Systems Engineering，2006，24(11):13 －18．

［10］马 成．基于期权契约的供应链协调问题研究［D］．合肥:合肥工业大学，2009．MA Cheng．Study on supply chain coordination based on option contracts［D］．Hefei:Hefei University of Industrial，2009．

［11］马士华，胡剑阳．一种基于期权的供应链能力预订模型［J］．管理工程学报，2004，18(1):8 －11．MA Shi-hua，HU Jian-yang．A model for supplier’s capacity ordering with options［J］．Journal Of Industrial Engineering and Engineering Management，2004，18(1):8－11．

［12］Rolf H．Capacity options for revenue management—theory and applications in the air cargo industry［D］．WHU Otto Beisheim School of Management，2006．

［13］赵明瑞，周 寒．航空货运的期权销售模式初探［J］．空运商务，2009(236):19－20．ZHAO Ming-rui，ZHOU Han．Study on the model of air cargo option．［J］．Air Transport Business，2009(236):19－20．

［14］王晓哲，杨静蕾．期权理论下的货运市场运力组织研究［J］．物流技术，2009，28(12):7 －9．WANG Xiao-zhe，YANG Jing-lei．Study on the transport capacity organization of the freight market based on option theory［J］．Logistics Technology，2009，28(12):7 －9．

［15］雷丽彩，周 晶．风险规避下的航空货运期权定价Stackelberg博弈模型［J］．系统工程理论与实践，2010，30(2):264 －271．LEI Li-cai，ZHOU Jing．Stackelberg game model of capacity options for air cargo under risk aversion［J］．Systems Engineering Theory ＆ Practice，2010，30(2):264 －271．