在役大跨石拱桥极限承载力的影响因素*
郭风琪,余志武
(中南大学土木工程学院,湖南长沙410075)
石拱桥是我国应用比较广泛的一种桥型,在对在役大跨度石拱桥进行分析和评估时,计算其极限承载力是考察桥梁工作性能的一个重要环节。影响结构极限承载力的因素众多,本文采用非线性有限元方法,考虑结构的材料非线性和几何非线性的双重影响,从荷载分布、温度影响、初始缺陷和结构损伤等几个方面对1座大跨度石拱桥的极限承载能力的影响进行研究,以便为役大跨度石拱桥的评估和加固设计提供有益的理论指导。
1 工程概况
某大跨度上承式石拱桥,主跨为120 m,腹拱为9孔13 m,桥宽8 m,全长241 m。主拱圈由两条分离式矩形石肋和8条钢筋混凝土横系梁组成,肋宽2.5 m,高1.6 m,主桥材料采用20 MPa小石子混凝土砌100 MPa块石。拱轴线为二次抛物线,矢跨比为1/5。大桥设计荷载为:汽车-15级,挂车-80。
2 有限元模型
有限元计算采用大型有限元程序ANSYS进行建模分析,模型采用8节点块体单元(SOLID65)建立。因拱上填料的材料和性质不明确,计算时未考虑其作用。将活荷载作用于腹拱圈上,主拱、腹拱与主拱墩固结处合并单元节点连接,全桥共划分为28 812个单元,有限元模型如图1所示。

图1 石拱桥有限元模型Fig.1 Finite element model of stone arch bridge
石砌体是一种非均质的、各向异性材料,砌缝是其薄弱环节,对其本构关系及破坏准则进行研究非常困难。到目前为止,还没有一个砌体应力应变关系和破坏准则被大多数人所接受[1]。然而,合理选取材料的弹塑性本构关系,对于非线性的有限元分析是非常重要的,这也是砌体结构非线性有限元分析的一个难点。对于ANSYS,能够反映砌体受砌缝影响的复杂的剪压破坏模型还不存在,只有参照类似材料的常用破坏准则,通过参数的适当选取来最大限度地模拟砌体的破坏。本文采用ANSYS提供的SOLID65单元所特有的CONCRETE材料来定义石砌体的强度准则。在此基础上,为解决材料的非线性问题,选取了多线性随动强化模型(MKIN)来定义石砌体的单轴应力应变曲线[2],该模型需要输入最多5个应力应变数据,从而得到具有石砌体材料特性的单元。单元的材料的参考相关文献的建议[3],峰值应变取 0.002,极限压应变取0.0033,峰值压应力取材料设计值20 MPa,单轴抗拉强度根据桥规确定为0.237 MPa。石砌体泊松比取0.255,裂缝闭合剪力传递系数取0.90,裂缝张开剪力传递系数取0.40。应力应变关系按本课题组提出的石砌体单轴受压本构关系表达式(1)所确定,相应曲线见图2。

图2 石砌体应力-应变曲线Fig.2 Stress-strain curve of stone masonry

式中:σf为石砌体的峰值应力;εf为石砌体的峰值应变。
3 极限承载力影响因素分析
3.1 荷载布置方式
本文采用双重非线性的方法进行极限承载力分析。在分析过程中,桥梁自重和二期恒载保持不变,活载根据桥梁设计规范,取为均布荷载加集中荷载的组合。当拱桥达到其极限承载力时,结构承受的总荷载为Pcr=Pd+λPc。式中:Pd为作用在拱桥上的恒载;Pc为作用在拱桥上的可变荷载;λ为拱桥破坏时所加可变荷载的倍数,称做极限活荷载系数。该桥原设计荷载等级为汽车 -15级,经过等效变换,在进行极限承载力分析时,取初始均布线荷载q0=3.1 kN/m,集中荷载P0=106.3 kN,相当于现行公路桥规中公路-I级荷载的0.3倍。在ANSYS分析时,为减小应力集中的现象,集中荷载处理为作用在几个单元上的面荷载。
为全面考察荷载分布的影响,顺桥向荷载荷载布置分为4个工况,详见表1。每个工况在横桥向又分为中载和偏载两种情况来计算。计算结果见表2。中载时的各工况极限活荷载系数与拱顶竖向位移的关系见图3。

表1 计算工况Table 1 Calculation conditions

表2 极限活荷载系数Table 2 Limit live load coefficients

图3 极限活荷载系数-拱顶竖向位移关系曲线Fig.3 Curves between limit live load coefficient and vault vertical displacement
由表2可以看出,对于均布荷载,无论集中荷载作用在拱顶或1/4跨,全跨施加均布荷载工况下极限活荷载系数均远大于半跨施加均布荷载工况下的极限活荷载系数,说明均布荷载全跨加载比半跨加载有利,这和石拱桥的一阶失稳模态(非对称失稳)也是相符的。同时,均布荷载全跨布置和半跨布置,其极限活荷载系数相差较大,说明均布荷载的分布对极限活荷载系数的影响较大。
对于集中荷载来说,无论均布荷载是半跨分布还是全跨分布,集中荷载布置在跨中工况下极限活荷载系数均比集中荷载布置在1/4跨位置的大,说明集中荷载布置在跨中比布置在1/4跨有利,这也与石拱桥一阶失稳模态(非对称失稳)相符。虽然集中荷载对极限活荷载系数的影响没有均布荷载大,但从不同工况下的结构破坏形态来看,其布置的位置对结构的最终破坏形态有较为直接的影响,是极限承载力分析中不可忽视的因素。
同时,各种偏载工况与相应的中载工况极限活荷载系数比值均小于1,但最小亦达到98.1%,说明偏载比中载对于结构的极限承载力不利,但影响非常有限,计算和评估时可以忽略。
3.2 温度的影响
公路桥涵设计通用规范(JTG D60—2004)中第4.3.10条规定,计算桥梁结构因均匀温度所产生的效应时,应考虑最高和最低有效温度。为使计算结果有利于对比,本文针对不同工况,各自与整体升、降同一温温差(±30℃)相组合,共形成8种含整体温度变化的组合。表3所示为结构在含整体温度变化的组合下极限活荷载系数计算结果。

表3 温度组合下极限活荷载系数Table 3 Limit live load coefficients under temperature combinations
由表3可见:当整体升温时,极限活荷载系数较原工况减小,说明升温对结构的极限承载力更为不利,而当整体降温时则有利,这与内力计算的结果相反。经分析,主要是由于升温时石砌体最不利截面的压应变更早达到极限压应变从而提前压碎的缘故。但无论升温还是降温,原结构的极限活荷载系数均不大于3.3%,变化较小,计算和评估时可以忽略。
3.3 结构初始缺陷
运营中的桥梁结构都会不同程度的存在力学缺陷和几何缺陷,石拱桥的几何缺陷主要由以下因素造成:在施工过程中,一是施工测量定位误差;二是拱架制作偏差;三是砌筑拱圈时,拱架变形与计算不符等;在桥梁运营过程中,一是基础产生沉降,二是超载车辆通行,三是自然或人为的破坏等。
因无主拱圈的线形实测数据,本文仅进行理论上的分析。几何缺陷的分布和值有很大的不确定性,目前,通常采用等效荷载法、直接缺陷分析法、一致缺陷模态法和随机缺陷法来考虑。考虑到一致缺陷模态法能够直接有效地考虑结构的不利缺陷模式的影响,本文分析时即采用该方法,将最低阶屈曲模态做为结构缺陷的分布方式研究缺陷对极限承载力的影响。初始几何缺陷取L/1 500,L/600,L/400共3种情况,计算结果见表4,相应比较曲线见图4。

表4 不同几何缺陷极限活荷载系数(矢跨比1/5,抛物线拱)Table 4 Limit live load coefficients under different geometric imperfections

图4 不同几何缺陷极限活荷载系数曲线Fig.4 Curves of limit live load coefficients under different geometric imperfections
由表4和图4可以看出:随着缺陷幅值的增大,结构极限承载力和拱顶竖向位移都不断下降,各自近似成比例关系,当石拱桥的初始缺陷为L/1500时,其极限活荷载系数降低7%~10%;当初始缺陷为L/400时,其极限活荷载系数降低30%~35%,可见初始缺陷对石拱桥的极限承载力影响较大,计算和评估时不可忽略。
3.4 结构损伤
石砌体材料内部分布有大量的微孔洞与微缺陷,其微观结构非常复杂。大跨度石拱桥在役使用多年后,这些微孔洞和微缺陷逐渐扩展从而形成较大的裂纹,同时也会有新的孔洞与裂纹不断萌生。由此导致材料的破坏机理非常复杂,精确的理论分析较为困难。为了便于研究,引入损伤程度的概念:在相同应变的情况下,有损伤材料有效应力与无损伤材料应力的比值(1-η)的来表征结构的材料完好程度,η即为结构的损伤程度[4]。这样,根据本文石砌体本构关系表达式(1),即可得到有损伤石砌体材料的本构关系表达式(2):
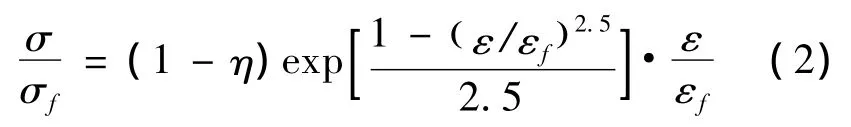
对前述大跨度石拱桥分别建立损伤程度为15%,30%和45%和60%时的考虑双重非线性的结构模型,并针对4种荷载工况进行极限承载力分析。在不同损伤程度下,极限活荷载系数见表5,相应比较曲线见图5。
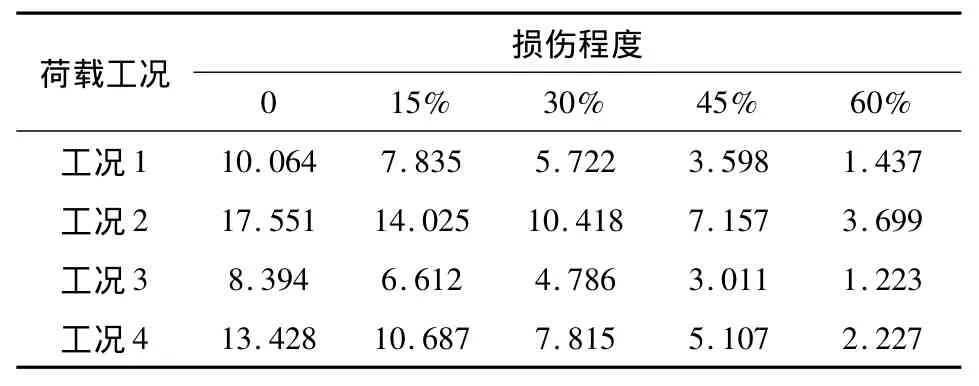
表5 不同损伤程度极限活荷载系数Table 5 Limit live load coefficients under different damage degree

图5 损伤程度-极限活荷载系数关系曲线Fig.5 Curve between damage degree and limit live load coefficient
从图5和表5可以看出:随损伤程度的增大,结构极限承载力基本上呈线性减小;当损伤为30%时,极限承载力下降已接近50%。因此,结构损伤对石拱桥的极限承载力影响较大,计算和评估时应计入其影响。
4 结语
(l)集中荷载的布置对极限承载力的影响不可忽视,作用在1/4跨位置比作用在跨中更为不利。
(2)均布荷载的布置对极限承载力的影响不可忽视,其半跨布置,是相对不利的工况。
(3)偏载比中载不利但差别较小,计算和评估时可不予考虑。
(4)升温对极限承载力不利,降温有利,但差别较小,计算和评估时可不予考虑。
(5)初始缺陷对石拱桥的极限承载力影响较大,计算和评估时不可忽略。
(6)结构损伤对石拱桥的极限承载力影响较大,计算和评估时应计入其影响。
[1]熊 峰,应付钊.非线性有限元法分析预应力砌体墙结构[J].四川大学学报,2000,32(3):16 -20.XIONG Feng,YING Fu-zhao.Non - linear analysis of prestressed masonry by finite element ethod[J].journal of sichuan ersity,2000,32(3):16 -20.
[2]周 岑,孙利民.钢筋混凝土结构弹塑性分析在ANSYS中的实现[C]//2002 ANSYS中国用户年会论文集.2002:464-468.ZHOU Cen,SUN Li-min.Realization of rc structure elasto-plastic analysis with ANSYS[D]//2002 ANSYS Chinese User Annual Meeting Symposium.2002:464 -468.
[3]李英民,韩 军,刘立平.ANSYS在砌体结构非线性有限元分析中的应用研究[J].重庆建筑大学学报,2006,28(5):90-96.LI Ying-min,HAN Jun,LIU Li-ping.Apolication of ANSYS to finite element analysis for nonlinear masonry structures[J].Journal of Chongqing Jianzhu University,2006,28(5):90-96.
[4]朱万成,赵启林,唐春安,等.混凝土断裂过程的力学模型与数值模拟[J].力学进展,2002,32(4):579-598.ZHU Wan-cheng,ZHAO Qi-lin,TANG Chun-an,et al.Mechanical model and numerical simulation of fractur eprocess[J].Advances In Mechanics,2002,32(4):579-598.

