基于量子LM神经网络和粗糙集的石油储层识别方法研究

孙惠芹，刘 松，刘南平

（1.天津职业大学 电子信息工程学院，天津 300410；2.电子信息职业技术学院 电子系，天津 300350；3.天津师范大学 物理与电子信息学院，天津 300387）

基于量子LM神经网络和粗糙集的石油储层识别方法研究

孙惠芹1，刘 松2，刘南平3

（1.天津职业大学 电子信息工程学院，天津 300410；2.电子信息职业技术学院 电子系，天津 300350；3.天津师范大学 物理与电子信息学院，天津 300387）

提出一种量子LM（Levenberg Marquardt，LM）神经网络与粗糙集相结合的智能识别方法，以替代传统的统计识别方法和工程应用中以单一智能控制为基础的识别方法.基于LM神经网络的技术方案可以整理测井定位数据，提高预测的准确性；量子计算具有并行和类映射的优势；通过削减冗余信息和简化信息量，粗糙集可以降低量子LM神经网络的复杂性，缩短数据处理时间，削减神经网络的负担.通过在石油储层识别实践中的应用证明：该方法可以有效提高计算速度和识别精度，降低成本.

量子LM神经网络；石油储层识别；粗糙集；测井数据；智能识别

石油储层位于地表深层，很难精确定位，但通过研究石油测井的特征，可以确定石油的储层位置.储层定位是一项储藏物理与流体力学相结合的现代科技项目，先进有效的储层定位可以帮助人们准确地开展石油勘探.测井曲线反映了储层岩性和物理特性，目前，根据测井曲线和储油层之间的对应关系可以构建确定未知储层含油量的一系列公式，但测井曲线数据信息的不完整性和不确定性增加了识别和预测的难度［1］.现有的数据统计识别方法具有数据量大、有效数据筛选困难、计算时间长的缺点；而对储层岩性某一参数进行智能控制的识别方法因数据属性单一，造成识别准确度较低.因此，本研究尝试采用神经网络、模糊控制和粗糙集等综合技术确定地下分层，预测储油层［2］.

目前，大多数算法只对一个或几个数据指标进行分析，不能囊括测井的整体性，因此不适于石油的储层定位［3］.由于函数逼近问题通常包含几百权的网络，因此采用LM神经网络算法最为快捷，且与弹性传播和梯度下降等算法相比误差较低［4］.量子计算可将多个经典计算同时完成，具有并行、类映射的特点［5］，所以，量子LM神经网络算法更适合于石油储层测井数据的计算.此外，在处理不完整、不确定、特别是不同类别的数据时，粗糙集理论具有超强的能力［6］，适合从众多不同数据中提取核心数据，削减冗余信息，简化信息量，从而极大地削减神经网络的负担［7］.因此，本研究提出应用量子LM神经网络和粗糙集的方法对石油储层进行定位，希望能够提高系统识别准确度，降低数据处理的复杂性，缩短计算时间，降低工程成本.

1 神经网络理论

1.1 LM神经网络

LM神经网络是由输入层、隐藏层和输出层组成的3层前馈网络，其结构如图1所示.

图1 LM神经网络的简化结构图Fig.1 Simplified structure of LM neural network

LM神经网络中，隐藏层节点T时段的输出函数为：

式（1）和式（2）中：W是输入层和隐藏层神经元间的连接权；V是隐藏层和输出层神经元间的连接权；θ是隐藏层的阈值；φ是输出层的阈值；X和Y是输入层节点和输出层节点间的输入向量；函数f是典型单调递增函数.

1.2 量子LM神经网络

1997年，Karayiannis等提出了基于多层激活功能的量子LM 神经网络（Quantum Levenberg－Marquardt Neural Network，Q－LM－NN）模型，即在量子理论中叠加了量子态的观念［11］.与径向基函数（Radical Basis Function，RBF）神经网络相比，量子LM神经网络在LM神经网络三层结构的隐藏层神经元激活函数中叠加了多个传统的激活函数，并与固有的模糊神经网络整合，用以提高系统的精确度.LM神经网络常用的传递函数为对数sigmoid函数（即logsig）、高斯函数和径向基函数等［8］，而量子LM神经网络在LM神经网络多层传递函数的基础上线性叠加了多个sigmoid函数，其多层传递函数的表达式为

图2 多层传递函数Fig.2 Transfer function of multi－layer

由图2可知，与只有2种状态的传统sigmoid函数相比，隐藏层神经元可划分为多层次的神经元，其多层传递函数可表达多个状态，每个叠加的sigmoid函数具有不同的量子差距，可由θs调整，因此不同的数据类型可以映射到相应的层次，使层次的划分具有更大的自由度.

量子LM神经网络具有2个训练步骤：首先要调整连接权，即将网络对应的输入数据映射到相应的类空间；然后公开类空间中模糊或不确定的信息，通过调整量子LM算法中网络权的量子差距θs完成数据映射.具体运算步骤如下：

步骤1：初始化网络权β、阈值θs和网络参数n，并设置允许误差ε；

步骤2：利用式（4）更新不同层神经元的权，

2 粗糙集

实际应用中，由于石油测井面临的最大问题是不确定性和不完备性，因此，准确判断由连续量化法得到的储层定位核心信息是否有效存在困难.作为描述不完备性和不确定性的一种工具，Pawlak首次提出了粗糙集［9］，而约简是粗糙集中一种有效替代筛选出的关键信息的重要方法，故本研究将粗糙集中的约简理论应用于核心数据的筛选.

2.1 约简的原理

属性约简是对系统类别和决策能力相关冗余信息的删减，以减少数据量，提高结果的准确性.

定义1 在一个信息系统K＝（U，R）中，U是域，R是条件属性集C和决策属性集D的组合，如果c∈C，定义属性c到D的相似值为

式（7）中：s值越大，表明c到D越相似；s值越小，表明c到D的差异性越大；如果s＝1，则c到D是完全相似的.

2.2 基于相似性的约简算法

步骤1：参照特定矩阵，计算core（C），其中C是由特定矩阵的所有单个属性组成的集.

步骤2：计算自由属性ci∈C（i＝1，2，…，k）到决策属性集D的相似值si（i＝1，2，…，k）.

步骤3：为了获得相对简单的约简，可构建1个自由属性到决策属性集D的相似值si（i＝1，2，…，k）的降序排列集合R，直到满足ind（R）＝ind（C），则R是相对简单的约简.信息约简的基本步骤为：

（1）离散化和归纳属性信息表，即对连续属性离散化，对特性属性进行归纳；

（2）删减冗余对象，得到信息表的约简；

（3）计算条件属性的核心；

（4）计算各自属性的相似值si，并计算最简单的约简表.

3 智能识别方法

由于量子LM神经网络信息识别系统具有高度的并行性，且信息约简的方法可以有效减少数据量［10］，因此，基于粗糙集和量子LM神经网络的石油储层定位方法可以通过约简训练样品全面代表储层信息.

3.1 石油储层识别系统

基于粗糙集和量子LM神经网络的石油储层识别系统的流程如图3所示.

图3 基于粗糙集和量子LM神经网络的储层识别系统的流程图Fig.3 Reservoir identification system flow char

（1）选择和预处理样品信息：样品信息直接反映储层信息，应尽可能全面、准确地对样品集进行分类.必须认真审核数据，保证所选测井数据不叠加.此外，样品分为训练样品和测试样品2类.

（2）离散和归纳属性：为了减少样品的属性，首先，提取样品并归纳到决策属性；然后，参考量子粒子群优化（Quantum Particle Swarm Optimization，QPSO）算法的离散连续属性［11］.

（3）由粗糙集删减样品信息：删除样品信息表中冗余的属性，找到核心并计算属性的相似度，确定反映条件属性特征的最简单约简表［12］.

（4）优化网络：减小样品集的训练，直至获得满意的相似度，得到可实现的历元数［13］.

（5）量子LM神经网络的鉴定与输出：参考条件属性，计算并优化预处理后储层信息的相关属性.依据量子LM神经网络识别分析这些属性，并最终输出结果.

3.2 应用实例

Dupo是一个典型的泥砂岩夹薄层储油环境复杂的地区，其石油储层位置很难确定，故可利用本研究提出的智能优化算法解决此问题.

在Dupo地区1 600～1 800m深度的一些关键位置，提取230个样品作为训练样品，其中包含80个储层样品和150个非储层样品.为了避免训练样品和测试样品的重复，样品数据依据均方根误差归一到［0，1］区间，用以代表决策属性集｛储层和非储层｝.样品信息共有41个条件属性，分别为RNML、RLML、R4、R25、DA、DAZ、RLS、RT、GR、SP、AC、RMLL、CAL、CNL、DEN、FF、FNUM、JIE、POR、PORW、PORT、PORF、PERM、SXO、RWA、RMFA、SH、CALI、SW、SWI、MD、KO、KW、PORA、PORD、PORN、VCO、SPC、BITS、RXO和JBQX，通过黄金分割进行优化，实现连续属性的离散化.

对41个条件属性进行预处理并离散化后，采用可辨矩阵得到样品属性约简以及与此相关的最简单的条件属性集｛RNML、LML、R4、R25、DA、RLS、RT、GR、SP、AC、RMLL、CNL、DEN、JIE、PORT、PORF、PERM、RWA、RMFA、SH、CALI、SWI、KO、KW、SPC｝，该属性集反映了储油层的特性.表1列出了25个样品属性约简的数值范围.

表1 样品属性约简数值范围表Tab.1 Sample attribute reduction range of values

根据式（1）对1 600～1 800m井段的上述25个样品属性进行规范化，如图4所示，其中，横轴表示深度，纵轴表示归一化的数值.

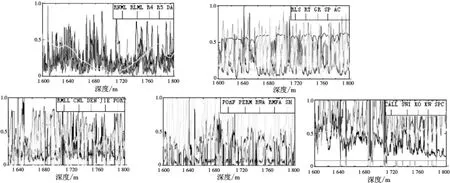
图4 25个属性归一化曲线Fig.4 25property normalized curve

反复优化确定总井段储层的预测模型，分别对 反 向 传 播 （Back Propagation，BP）算 法、LM神经网络算法和量子LM神经网络算法的均方根误差（RMSE）、最大正误差（MAXPE）和最大负误差（MAXNE）进行对比，结果如表2所示.

表2 性能指标表Tab.2 Performance indexes data

BP算法构建了“25－16－1”的网络结构，学习因数为0.05；LM神经网络算法构建了“25－13－1”的网络结构.2种算法隐藏层和输出层的传递函数均采用f（x）＝（1－e－x）（1＋e－x）.量子LM 神经网络算法采用3层传递函数，量子数n＝2，梯度因子β＝16，在重复实验的基础上，输出层的学习率η＝0.5.图5为网络的训练误差曲线.

图5 3种算法的训练误差曲线Fig.5 Training error curve of three algorithms

由图5可知，在性能指标方面（如识别率），量子LM神经网络算法均优于BP算法和LM算法.过拟合现象、维数和局部最小值的限制从本质上削弱了传统BP算法和LM算法的功能，量子LM神经网络算法可以有效避免上述不足.此外，量子LM神经网络算法具有改善识别精度，提高计算速度和规范能力的优势.

图6显示了量子LM神经网络算法对1 600～1 800m井段的鉴定结果.

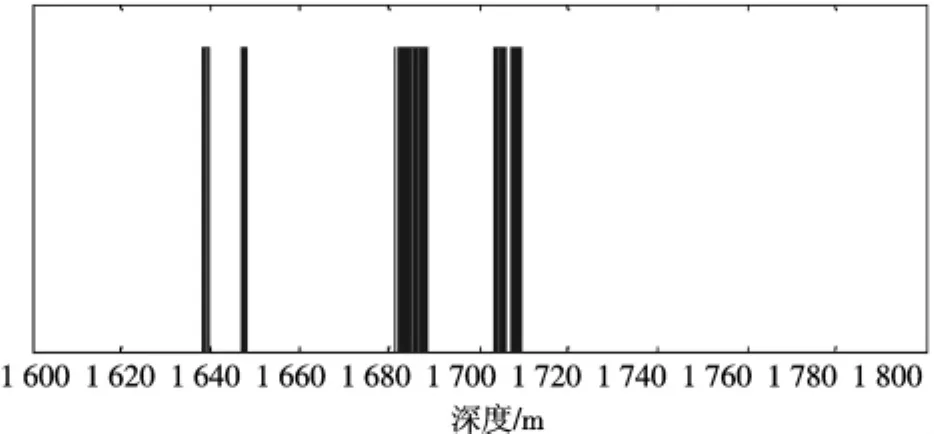
图6 量子LM神经网络算法对储油层鉴定结果图Fig.6 Q－LM－NN algorithm for reservoir identification results

图6中结果表明：深度分别为1 638.4～1 639.5m、1 646.8～1 648m、1 681.25～1 688.75m、1 703.6～1 706m和1 707.25～1 710m的5层为石油储层，其他部分为非储层.结果与试油结论基本吻合，证实了量子LM神经网络算法可以有效解决样品数据量过大的问题.

4 结论

基于粗糙集和量子LM神经网络设计了一种石油储层识别方法，该方法利用粗糙集删减冗余信息，简化了训练集；并通过量子LM神经网络算法中的多层传递函数删减了隐藏层，简化了计算过程.在Dupo复杂地区石油储层位置识别的应用中，识别预测数据与试油结论基本吻合，证明基于量子LM神经网络与粗糙集相结合的石油储层智能识别方法可以有效解决测井三维信息量过大、准确度低等问题，且系统运算速度快、识别准确度高，极大地降低了工程成本.

［1］ BABUSIAUX D.Oil and Gas Exploration and Production：Reserves，Costs，Contracts［M］.Paris：Editions Technip，2007：65－72.

［2］ KAMALI M.R.，MIRSHADY A A.Total organic carbon content determined from well logs usingΔlogR and neuro fuzzy techniques［J］.Journal of Petrolcum Science and Engineering，2004，45：141－148.

［3］ HAGAN M T，DEMUTH H B，BEALE M H.Neural Network Design［M］.Boston：PWS Pub Co，1995：158－165.

［4］ MAJDI A，BEIKI M，PIRAYEHGAR A.Identification of well logs with significant impact on prediction of oil and gas reservoirs permeability using statistical analysis of RSE values［J］.Journal of Petroleum Science and Engineering，2010，75：91－99.

［5］ KARIMPOULIA S，FATHIANPOURA N，ROOHIB J.A new approach to improve neural networks algorithm in perme－ability prediction of petroleum reservoirs using supervised committee machine neural network［J］.Journal of Petroleum Science and Engineering，2010，73：227－234.

［6］ HAO L N，WANG W，WU G Y.Research on rough set－neural network fault diagnosis method［J］.Journal of Northeastern University，2003（3）：46－49.

［7］ PAWLAK Z.Rough Sets－theoretical Aspects of Reasoning A－bout Data［M］.Dordrecht：Kluwer Acadermic Publishers，1991：135－142.

［8］ PURUSHOTHAMAN G，KARAYIANNIS N B.Quantum neural networks（QNNs）：Inherently fuzzy feedforward neural networks［J］.IEEE Transactions on Neural Networks，1997，8（3）：679－693.

［9］ PAWLAK Z.Rough sets［J］.International Journal of Computer＆Information Sciences，1982，11（5）：341 －356.

［10］ NIELSEN M A，CHUANG I.Quantum computation and quantum information［J］.American Journal of Physics，2002，70（5）：558－589.

［11］ LUITEL B，VENAYAGAMOORTHY G K.Quantum inspired PSO for the optimization of simultaneous recurrent neural networks as MIMO learning systems［J］.Neural Net Works，2010，23（5）：583－586.

［12］ MICHALAK K，KWASNICKA H.Correlation－based feature selection method［J］.International Journal of Bio－Inspired Computation，2010，2（5）：319－332.

［13］ LAALAOUI Y，DRIAS H.ACO approach with learning for preemptive scheduling of real－time tasks［J］.International Journal of Bio－Inspired Computation，2010，2（6）：383－394.

Research on oil reservoir identification method based on quantum LM neural network and rough set

SUNHui－qin1，LIUSong2，LIUNan－ping3
（1.School of Electronic and Information Engineering，Tianjin Vocational Institute，Tianjin 300410，China；
2.Department of Electronic，Electronic Information Vocational Technology College，Tianjin 300350，China；
3.College of Physics and Electronic Information Science，Tianjin Normal University，Tianjin 300387，China）

An intelligent identification method of oil reservoir based on quantum Levenberg－Marquardt（LM）neural network and rough set is presented，substituting traditional statistical identification methods and the method based on a single intelligent control in engineering applications.The technical solutions based on LM neural network can organize the logging location data to improve the accuracy of prediction.Quantum calculation has the advantages of parallel and class mapping.By reducing the redundant information and simplifying the information content，rough set can reduce the complexity of quantum LM neural network，shorten the data processing time and lighten the burden of neural network.The method is applied to the practice of oil reservoir identification，and it is proved that it can improve the calculating speed and identification precision，and reduce the cost.

quantum LM neural network；oil reservoir identification；rough sets；logging data；intelligent identification

TE19

A

1671－1114（2012）03－0045－06

2011－03－16

中国博士后基金资助项目（20090450750）

孙惠芹（1968—），女，副教授，主要从事电子通信方面的研究.

（责任编校 亢原彬）